DETERMINANTES Matria Dada Matria Estudada Difcil tudo aquilo

DETERMINANTES Matéria Dada é Matéria Estudada!!! “Difícil é tudo aquilo que eu AINDA não sei fazer”

Determinantes Determinante é um número real associado a uma matriz quadrada. Notação: det A ou |A|. Determinante de uma Matriz Quadrada de 1ª Ordem. Seja a matriz A = (a 11). O determinante de A será o próprio elemento a 11. A = ( 3 ) , logo | A | = 3

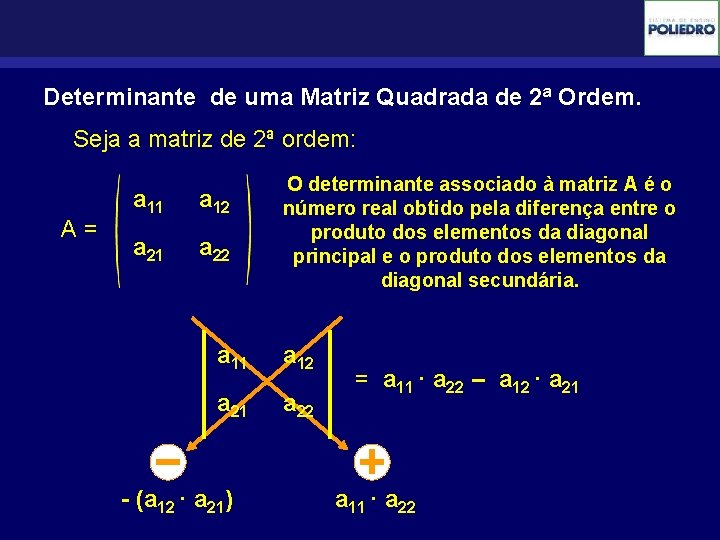
Determinante de uma Matriz Quadrada de 2ª Ordem. Seja a matriz de 2ª ordem: A= a 11 a 12 a 21 a 22 O determinante associado à matriz A é o número real obtido pela diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária. a 11 a 12 a 21 a 22 - (a 12 · a 21) = a 11 · a 22 – a 12 · a 21 a 11 · a 22

Determinante de uma Matriz Quadrada de 2ª Ordem. Ex: 1) 7 2 3 5 - = 7. 5 - 2. 3 = 29 +

Ex: 2)

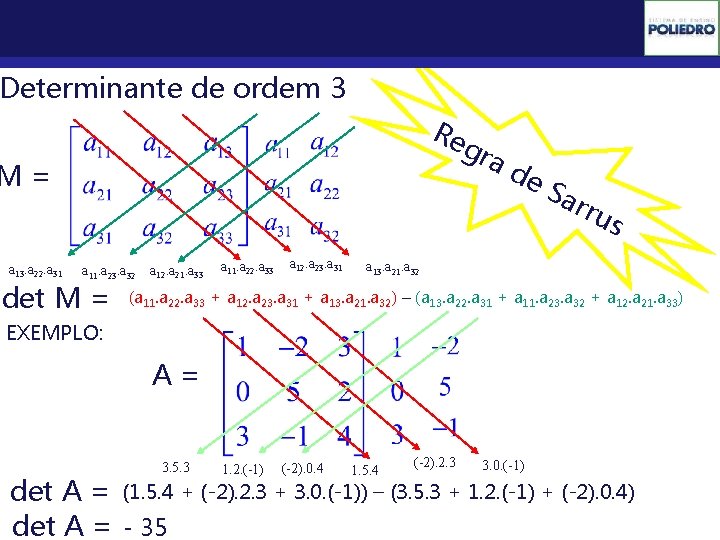
Determinantes Determinante de ordem 3 Re gra M= a 13. a 22. a 31 a 11. a 23. a 32 det M = a 12. a 21. a 33 a 11. a 22. a 33 a 12. a 23. a 31 de Sa rru s a 13. a 21. a 32 (a 11. a 22. a 33 + a 12. a 23. a 31 + a 13. a 21. a 32) – (a 13. a 22. a 31 + a 11. a 23. a 32 + a 12. a 21. a 33) EXEMPLO: A= 3. 5. 3 1. 2. (-1) (-2). 0. 4 1. 5. 4 (-2). 2. 3 3. 0. (-1) det A = (1. 5. 4 + (-2). 2. 3 + 3. 0. (-1)) – (3. 5. 3 + 1. 2. (-1) + (-2). 0. 4) det A = - 35

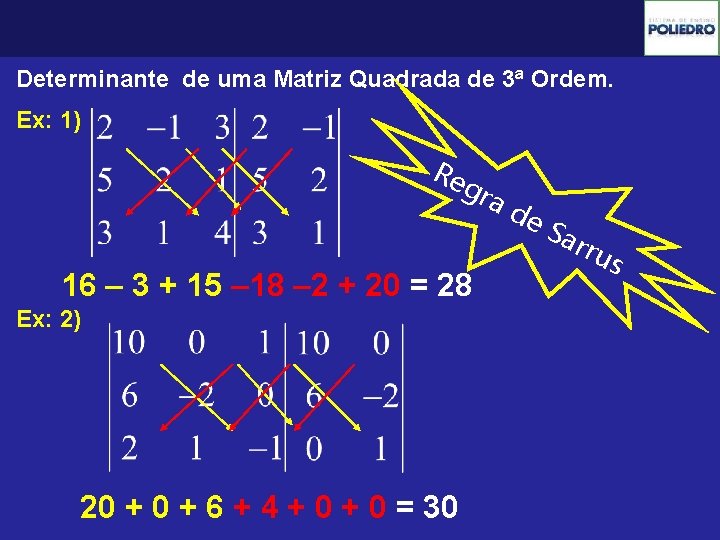
Determinante de uma Matriz Quadrada de 3ª Ordem. Ex: 1) Re gra 16 – 3 + 15 – 18 – 2 + 20 = 28 Ex: 2) 20 + 6 + 4 + 0 = 30 de Sa rru s

Determinantes Teorema Fundamental (Laplace) • Menor Complementar Dada uma matriz quadrada A, chamamos menor complementar do elemento aij, e indicamos por Dij, o determinante da matriz quadrada de ordem n – 1, que se obtém suprimindo a linha i e a coluna j da matriz A. A= D 11 =

Determinantes Teorema Fundamental (Laplace) • Menor Complementar A= D 23 =

Determinantes Teorema Fundamental (Laplace) • Co-fator Chamamos co-fator do elemento aij, e indicamos com Aij, o número (– 1)i+j · Dij, em que Dij é o menor complementar de aij. Aij = (-1)i+j. Dij A= A 11 = (-1)1+1. D 11 = (-1)2.

Determinantes Teorema Fundamental (Laplace) • Cofator A= Matriz cofator Cof A= Aij = (-1)i+j. Dij

Determinantes Teorema Fundamental (Laplace) • Determinante de uma matriz de ordem n O determinante de uma matriz quadrada de ordem n, , é a soma dos o número (– 1)i+j · Dij, em que Dij é o menor complementar de aij. det A = a 11. A 11 + a 21. A 21 + a 31. A 31 A= det A = a 21. A 21 + a 22. A 22 + a 23. A 23 det A = a 31. A 31 + a 32. A 32 + a 33. A 33

Determinantes Regra de Chió A regra de Chió é uma técnica utilizada no cálculo do determinantes de ordem n 2. Dada uma matriz A de ordem n, ao aplicarmos essa regra obteremos uma outra matriz A´ de ordem n – 1, cujo determinante é igual ao de A. 1. Desde que a matriz tenha um elemento igual a 1 (um), eliminamos a linha e a coluna deste elemento. 2. Subtraímos de cada elemento restante o produto dos dois elementos eliminados, que pertenciam à sua linha e à sua coluna. 3. Multiplicamos o determinante obtido por (-1)i + j, em que i e j representam a linha e a coluna retiradas. Ex. : -17

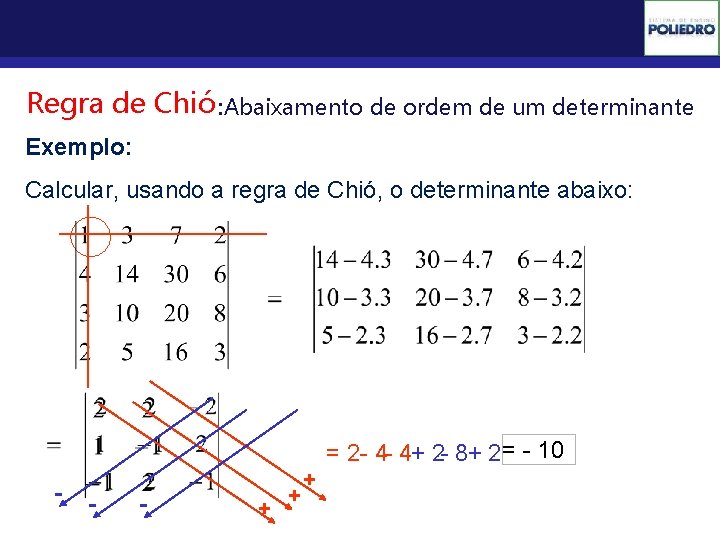
Determinantes Regra de Chió : Abaixamento de ordem de um determinante Exemplo: Calcular, usando a regra de Chió, o determinante abaixo: - - - + + + = 2 - 4 - 4+ 2 - 8+ 2= - 10

Determinantes Exemplo: Se o determinante não tiver nenhum elemento unitário podemos dividir uma das filas (linha ou coluna) para obtermos um elemento unitário, mas devemos multiplicar o determinante obtido por este valor para não haver alteração do resultado = 3. (-10) = -30

Determinantes Matriz de Vandermonde Chamamos matriz de Vandermonde, ou das potências, toda matriz de ordem n 2, em que suas colunas são potências de mesma base, com expoente inteiro, variando de 0 à n – 1 (os elementos de cada coluna formam uma progressão geométrica de primeiro termo igual a 1). Obs. : Os elementos da 2ª linha são chamados elementos característicos da matriz. O determinante da matriz de Vandermonde é igual ao produto de todas as diferenças possíveis entre os elementos característicos e seus antecessores. Ex. : (3 – 2)(5 – 3)(7 – 2)(7 – 3)(7 – 5) 1. 3. 2. 5. 4. 2 240

Determinantes OBSERVAÇÕES: 1) Uma matriz quadrada A diz-se REGULAR ou NÃO-SINGULAR se det A ≠ 0. 2) Uma matriz quadrada somente é INVERTÍVEL se for regular. 3) Uma matriz quadrada invertível diz-se ORTOGONAL somente se sua transposta for igual à sua inversa.

Exercícios de Sala Solução

Exercícios de Sala

Exercícios de Sala

Exercícios de Sala

“Que a força esteja com você”