DepthFirst Non Derivable Itemset Mining Toon Calders Bart

Depth-First Non. Derivable Itemset Mining Toon Calders , Bart Goethals Proceeding of SDM 2005 Speaker: Pei-Min Chou Date: 2005/11/4 1

Introduction l Breadth-first: Apriori algo. l l l Large : all frequent itemsets Scan over database Depth-first l Condensed representation 2

Non-derivable l Derivable l l Support completely determined by its subsets Redundant information Ex. If {a, b}, {a, c}, {b, c}=2, then {a, b, c}= 2 Non-derivable l concise and smaller 3

Deduction Rules l l l Compute the lower and upper bound Si is derivable l lower bound =upper bound=support Si is non-derivable l Support>threshold l Lower bound != upper bound Lower bound Upper bound 4

Example of Deduction Rules DB TID Items 1 a, b, c 2 a, c , d 3 a, b , d 4 c , d 5 b , c , d 6 a, b 7 b, d 8 b, c , d 9 b , c , d 10 A, b, c, d 5

Ex. of Deduction Rules(cont) 1 1 1 1 0 0 2 2 2 4 6

df. NDI Algorithm l l l Combine Eclat, d. Eclat diffsets and deduction rule. Reverse pre-order Use tid-list to compute support Store the min{ Eclat, d. Eclat } 7

Eclat Algorithm l l l First algorithm for frequent itemsets with depthfirst Intersection the tid-list Ex. tid-list table a b c d e 1 2 3 6 7 8 1 2 3 5 6 9 10 1 2 4 7 9 1 3 5 8 10 3 4 5 6 7 8 9 10 8

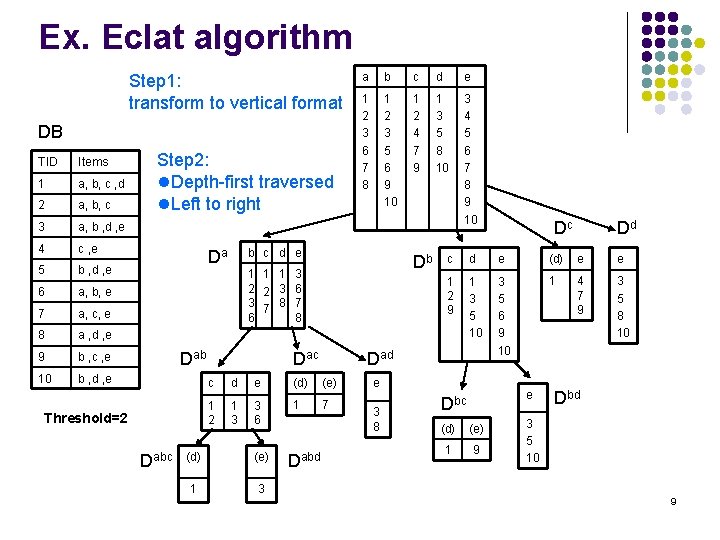
Ex. Eclat algorithm Step 1: transform to vertical format DB TID Items 1 a, b, c , d 2 a, b, c 3 a, b , d , e 4 c , e 5 b , d , e 6 a, b, e 7 a, c, e 8 a , d , e 9 b , c , e 10 b , d , e Step 2: l. Depth-first traversed l. Left to right a b c d e 1 2 3 6 7 8 1 2 3 5 6 9 10 1 2 4 7 9 1 3 5 8 10 3 4 5 6 7 8 9 10 b c d e Da Db 1 1 1 3 2 2 3 6 3 7 8 7 6 8 Dab Threshold=2 Dabc Dac d e (d) (e) 1 2 1 3 3 6 1 7 (d) (e) 1 3 Dabd d e (d) e e 1 2 9 1 3 5 10 3 5 6 9 10 1 4 7 9 3 5 8 10 e 3 8 Dd c Dad c Dc e Dbc (d) (e) 1 9 Dbd 3 5 10 9

Reordering l l Order the items in support ascending. Effect l l l Reduced number of candidate itemsets. Generating sets have lower support if tid-list are small. At most all k-itemsets with the same k-1 prefix stored in main memory. 10

Ex. Eclat algo. with reordering Sorted DB Threshold=2 Dc c d a b e 1 2 4 7 9 1 3 5 8 10 1 2 3 6 7 8 1 2 3 5 6 9 10 3 4 5 6 7 8 9 10 Dd (d ) a b e 1 1 2 7 1 2 9 4 7 9 Dca Dcb a b e 1 3 8 1 3 5 10 3 5 8 10 Da Ddb Db b e e 1 2 3 6 7 8 3 5 6 9 10 Dab (e) b e e e 7 12 9 1 3 3 8 3 5 10 3 6 Ddab (e) 3 11

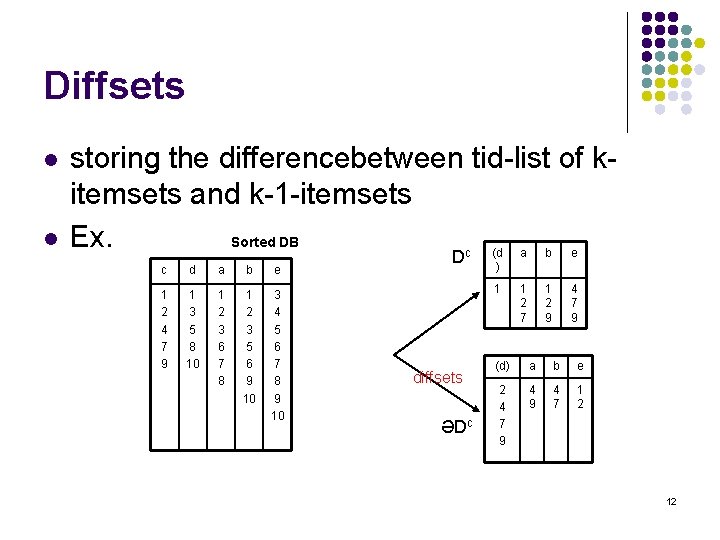
Diffsets l l storing the differencebetween tid-list of kitemsets and k-1 -itemsets Ex. Sorted DB c d a b e 1 2 4 7 9 1 3 5 8 10 1 2 3 6 7 8 1 2 3 5 6 9 10 3 4 5 6 7 8 9 10 Dc diffsets ӘDc (d ) a b e 1 1 2 7 1 2 9 4 7 9 (d) a b e 2 4 7 9 4 7 1 2 12

Ex. d. Eclat algo. with reordering Sorted DB ӘDc ӘDd (d) a b e 2 4 7 9 4 7 1 2 5 10 8 1 ӘDca ӘDcb ӘDa ӘDdb ӘDb b e e 7 1 8 2 1 2 ӘDab (e ) b (e) b e e e 8 1 1 1 2 7 1 2 ӘDdab (e) 1 13

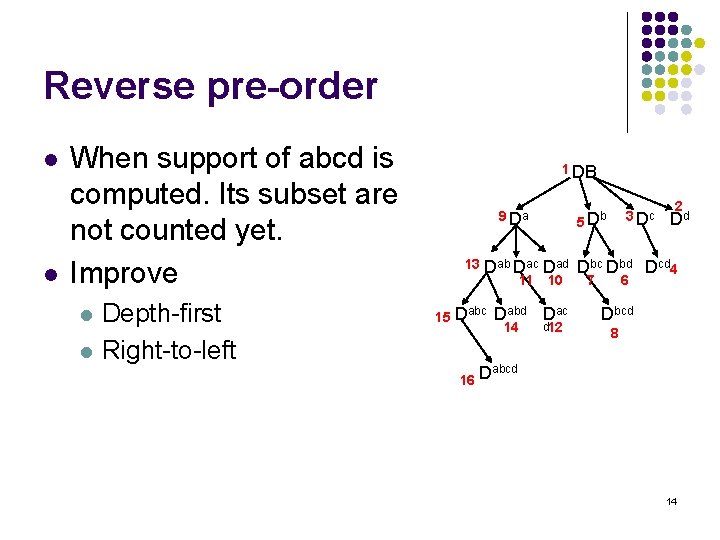
Reverse pre-order l l When support of abcd is computed. Its subset are not counted yet. Improve l l Depth-first Right-to-left 1 DB 9 Da 5 13 Dab Dac Dad 11 10 15 Dabc 16 D Dabd Dac 14 d 12 3 Dc Db 2 Dd Dbc Dbd Dcd 4 7 6 Dbcd 8 abcd 14

df. NDI Algorithm(thesis. ) l Theorem: l l If Itemset is derivable, then its superset as well. If item with brackets l l Infrequent Supp(i)=Li or supp(I)=Ui l l i: non-derivable i’s superset is derivable 15

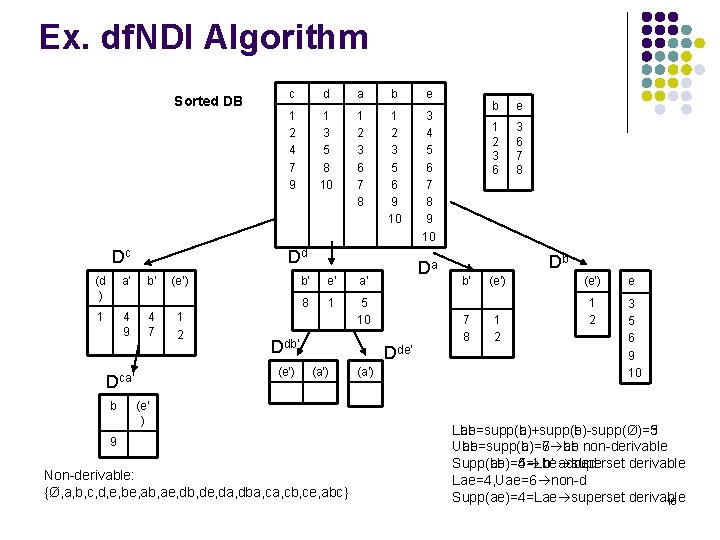
Ex. df. NDI Algorithm Sorted DB Dc (d ) a’ 1 4 9 d a b e 1 2 4 7 9 1 3 5 8 10 1 2 3 6 7 8 1 2 3 5 6 9 10 3 4 5 6 7 8 9 10 Dd b’ 4 7 (e’) 1 2 b’ e’ a’ 8 1 5 10 Ddb’ (e’) Dca’ b c Da Dde’ (a’) (e’ ) 9 Non-derivable: {Ø, a, b, c, d, e, be, ab, ae, db, de, da, dba, cb, ce, abc} (a’) b e 1 2 3 6 7 8 Db b’ 7 8 (e’) 1 2 (e’) e 1 2 3 5 6 9 10 Lab=supp(a)+supp(b)-supp(Ø)=3 Lbe=supp(b)+supp(e)-supp(Ø)=5 Ube=supp(b)=7 be non-derivable Uab=supp(a)=6 ab Supp(be)=5=Lbe superset Supp(ab)=4 b’ added derivable Lae=4, Uae=6 non-d Supp(ae)=4=Lae superset derivable 16

Experiment l l 1. 5 GHz Pentium IV PC with 1 GB of main memory Test datasets 17

Performance 18

Memory usage 19