Data Analysis I Peter Fox Data Science ITWSCSCIERTH43506350

Data Analysis I Peter Fox Data Science – ITWS/CSCI/ERTH-4350/6350 Module 4, September 26, 2017 1

Contents • • • Preparing for data analysis Completing and presenting results Statistics Distributions Filtering, etc. 2

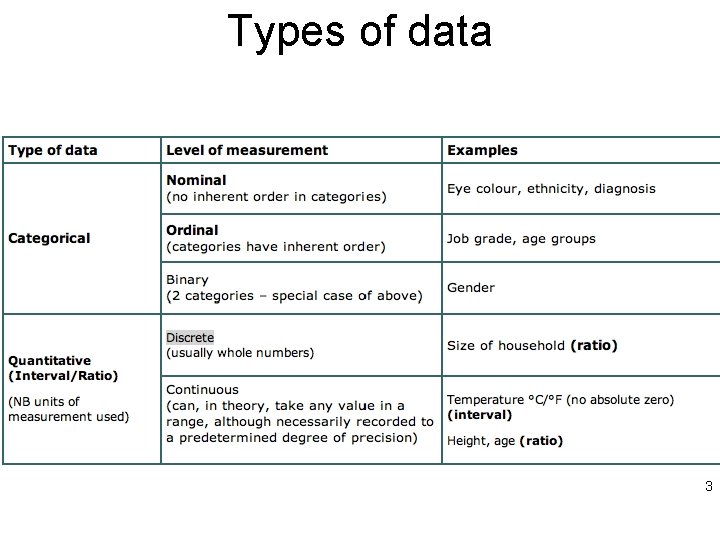
Types of data 3

Data types • Time-based, space-based, image-based, … • Encoded in different formats • May need to manipulate the data, e. g. – In our Data Mining tutorial and conversion to ARFF – Coordinates – Units – Higher order, e. g. derivative, average 4

Induction or deduction? • Induction: The development of theories from observation – Qualitative – usually information-based • Deduction: The testing/application of theories – Quantitative – usually numeric, data-based 5

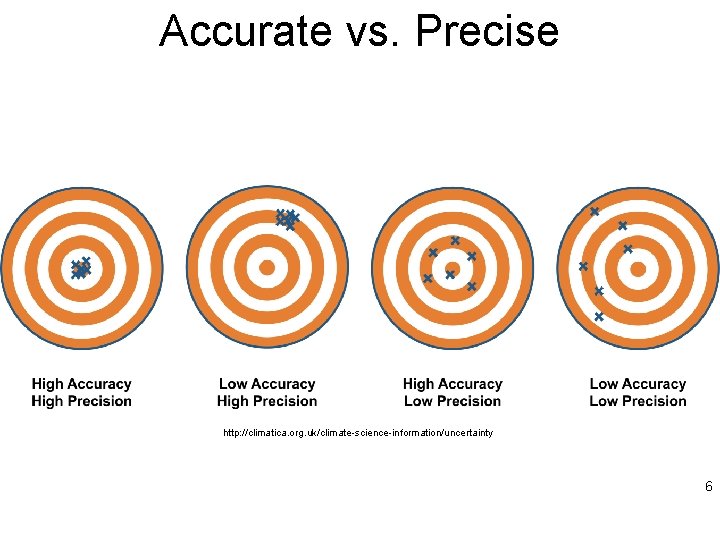
Accurate vs. Precise http: //climatica. org. uk/climate-science-information/uncertainty 6

‘Signal to noise’ • Understanding accuracy and precision – Accuracy – Precision • Affects choices of analysis • Affects interpretations (g-i-g-o) • Leads to data quality and assurance specification • Signal and noise are context dependent 7

Other considerations • Continuous or discrete • Underlying reference system • Oh yeah: metadata standards and conventions • The underlying data structures are important at this stage but there is a tendency to read in partial data – Why is this a problem? – How to ameliorate any problems? 8

Outlier • An extreme, or atypical, data value(s) in a sample. • They should be considered carefully, before exclusion from analysis. • For example, data values maybe recorded erroneously, and hence they may be corrected. • However, in other cases they may just be surprisingly different, but not necessarily 'wrong'. 9

Special values in data • • Fill value Error value Missing value Not-a-number Infinity Default Null Rational numbers 10

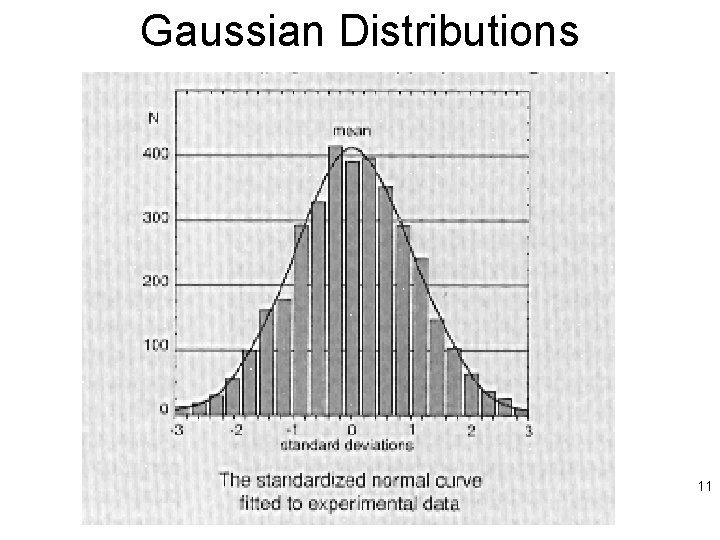
Gaussian Distributions 11

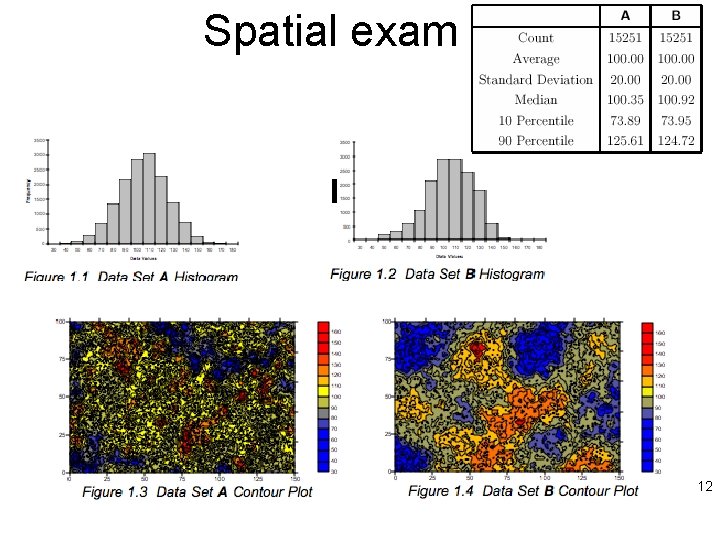
Spatial example 12

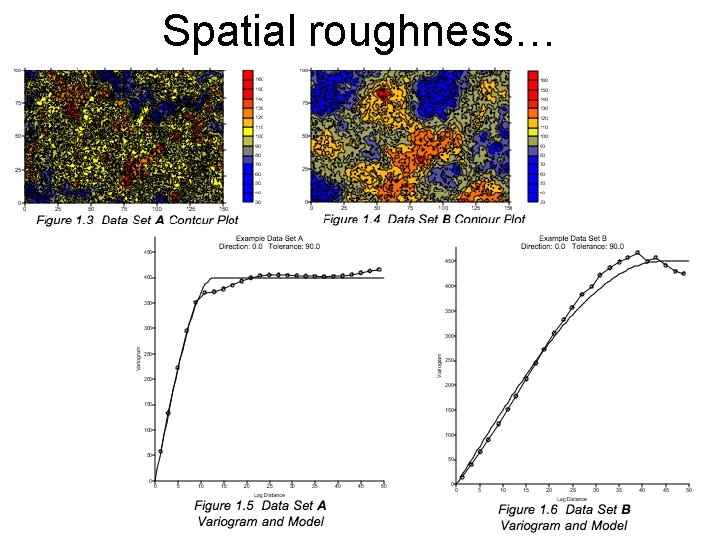
Spatial roughness… 13

Statistics • We will most often use a Gaussian distribution (aka normal distribution, or bellcurve) to describe the statistical properties of a group of measurements. • The variation in the measurements taken over a finite spatial region may be caused by intrinsic spatial variation in the measurement, by uncertainties in the measuring method or equipment, by operator error, . . . 14

Mean and standard deviation • The mean, m, of n values of the measurement of a property z (the average). – m = [ SUM {i=1, n} zi ] / n • The standard deviation s of the measurements is an indication of the amount of spread in the measurements with respect to the mean. – s 2 = [ SUM {i=1, n} ( zi - m )2 ] /n • The quantity s 2 is known as the variance of the measurements. 15

Width of distribution • If the data are truly distributed in a Gaussian fashion, 65% of all the measurements fall within one s of the mean: i. e. the condition –s-m<z<s+m • is true about 2/3 of the time. • Accordingly, the more spread the measurements are away from the mean, the larger s will be. 16

Measurement description – by its mean and standard deviation. • Often a measurement at a sampling point is made several times and these measurements are grouped into a single one, giving the statistics. • If only a single measurement is made (due to cost or time), then we need to estimate the standard deviation in some way, perhaps by the known characteristics of our measuring device. • An estimate of the standard deviation of a measurement is more important than the measurement itself. 17

Weighting • In interpolation, the data are often weighted by the inverse of the variance ( w = s-2 ) when used in modeling or interpolations. In this way, we place more confidence in the betterdetermined values. • In classifying the data into groups, we can do so according to either the mean or the scatter or both. • Excel has the built-in functions AVERAGE and STDEV to calculate the mean and 18 standard deviation for a group of values.

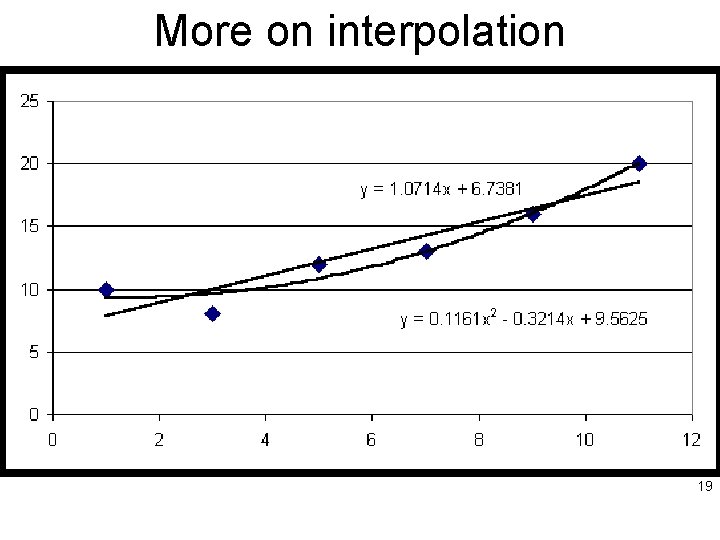
More on interpolation 19

Global/ Local Methods • Global methods ~ in which all the known data are considered • Local methods ~ in which only nearby data are used. • Local methods and most often the global methods also rely on the premise that nearby points are more similar than distant points. • Inverse Distance Weighting (IDW) is an example of a global method. 20

More… • Local methods include bilinear interpolation and planar interpolation within triangles delineated by 3 known points. • Global Surface Trends: Fitting some form of a polynomial to data to predict values at unsampled points. • Such fitting is done by regression – estimates of coefficients by least-squares fit to data. – Produces a continuous field – Continuous first derivatives – Values NOT reproduced exactly at observation points 21

Geospatial means x and y • In two spatial dimensions (map view x-y coordinates) the polynomials take the form: – f(x, y) = SUM r+s <= p ( brs xr ys ) • where b represents a series of coefficients and p is the order of the polynomial trend surface. • The summation is over all possible positive integers r and s such that their sum is less than or equal to the polynomial order p. 22

p=1 / p=2 • For example, if p =1, then – f(x, y) = b 00 + b 10 x + b 01 y – which is the equation of a plane. • If p = 2, then – f(x, y) = b 00 + b 10 x + b 01 y + b 11 x y + b 20 x 2 + b 02 y 2 • For a polynomial order p the number of coefficients is (p+1)(p+2)/2. In trend analysis or smoothing, these polynomials are estimated by regression. 23

Regression • Is the process of finding the coefficients that produce the best-fit to the observed values. • Best-fit is generally described as minimizing the squares of the misfits at each point, that is, – SUM {i=1, n} [ fi(x, y) – zi(x, y) ]2 • i. e. it is minimized by the choice of coefficients (this minimization is commonly called least-squares). 24

Coefficients • To estimate the coefficients we need at least as many or preferably more observations as coefficients. Otherwise? Underdetermined! • Once we estimate the coefficients, the surface trend is defined everywhere. • NB. The Excel function LINEST can be used to solve for the coefficients. 25

Choices… • The choice of how many coefficients to use (the order of the polynomial) depends on how smooth you think the variations in the property is, and on how well the data are fit by lower order polynomials. • In general, adding coefficients always improves the fit to the data to the extreme that if the number of coefficients equals the number of observations, the data can be fit perfectly. 26 • But this assumes that the data are perfect.

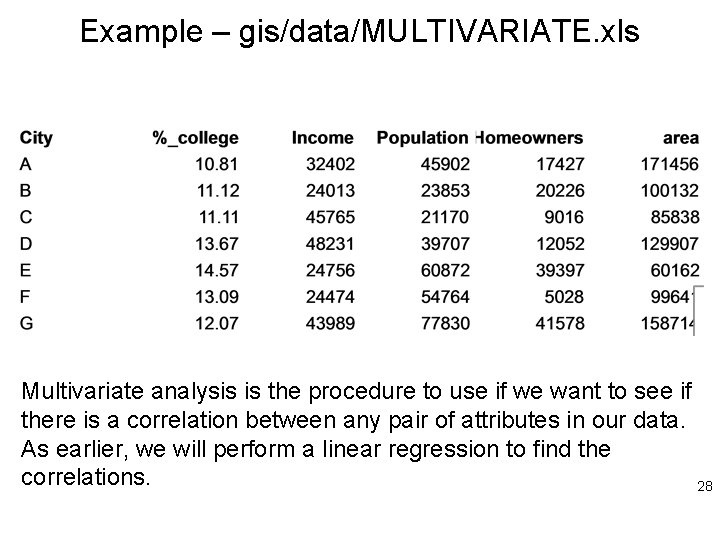
Multi-variate analysis • Multivariate analysis is the procedure to use if we want to see if there is a correlation between any pair of attributes in our data. • As earlier, you perform a linear regression to find the correlations. 27

Example – gis/data/MULTIVARIATE. xls Multivariate analysis is the procedure to use if we want to see if there is a correlation between any pair of attributes in our data. As earlier, we will perform a linear regression to find the correlations. 28

Analysis – i. e. Science question • We want to see if there is a correlation between the percent of the college-educated population and the mean Income, the overall population, the percentage of people who own their own homes, and the population density. • To do so we solve the set of 7 linear equations of the form: • %_college = a x Income + b x Population + c x Homeowners/Population + d x Population/area + e 29

• We solve for the coefficients a through e. • This is done with Excel with the LINEST function, giving the result: – Revealing that population density correlates with college-educated percentage at a significant level. – => college-educated people prefer to live in densely populated cities. 30

Bi-linear Interpolation • In two-dimensions we can interpolate between points in a regular or nearly regular grid. • This interpolation is between 4 points, and hence it is a local method. – Produces a continuous field – Discontinuous first derivative – Values reproduced exactly at grid points 31

Example x 0, y 0 t = [ x 0 – x 1 ] / [ x 2 - x 1 ] and u = [ y 0 – y 1 ] / [ y 4 - y 1 ] • The red squares represent 4 known values of z(x, y) and our goal is to estimate the value of z at the new point (blue circle) at (x 0, y 0). 32

Calculating… • Let • t = [ x 0 – x 1 ] / [ x 2 - x 1 ] and • u = [ y 0 – y 1 ] / [ y 4 - y 1 ] i. e. the fractional distances the new point is along the grid axes in x and y, respectively, where the subscripts refer to the known points as numbered above. Then • z (x 0 , y 0 ) = (1 -t) (1 -u) z 1 + t (1 -u) z 2 + t u z 3 + (1 -t ) u z 4 33

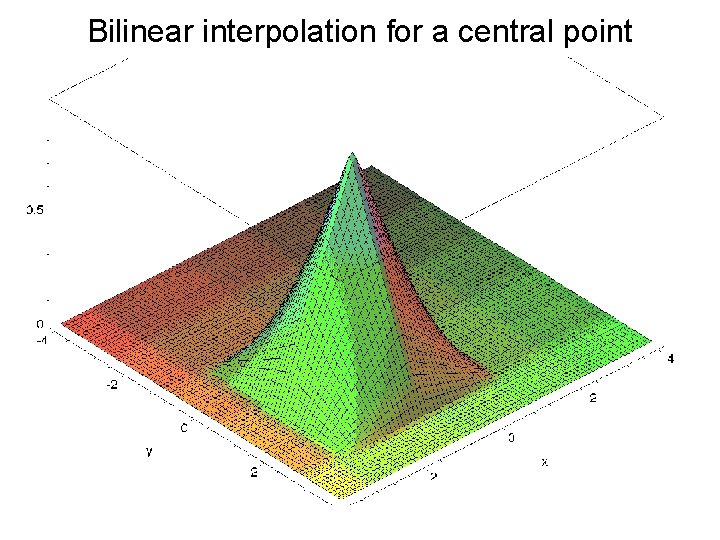
Bilinear interpolation for a central point 34

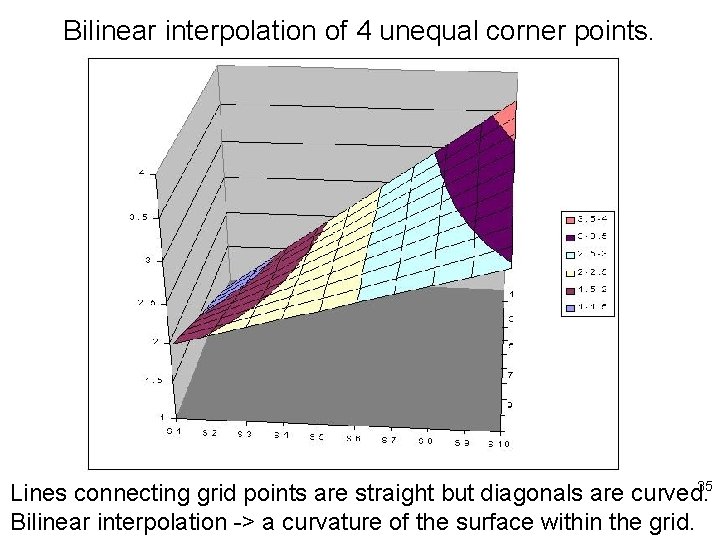
Bilinear interpolation of 4 unequal corner points. 35 Lines connecting grid points are straight but diagonals are curved. Bilinear interpolation -> a curvature of the surface within the grid.

Other interpolation • Delaunay triangles: sampled points are vertices of triangles within which values form a plane. • Thiessen (Dirichlet / Voronoi) polygons: value at unknown location equals value at nearest known point. • Splines: piece-wise polynomials estimated using a few local points, go through all known points. 36

More … • Bicubic interpolation – Requires knowing z (x, y) and slopes dz/dx, dz/dy, d 2 z/dxdy at all grid points. • Points and derivatives reproduced exactly at grid points • Continuous first derivative • Bicubic spline – Similar to bicubic interpolation but splines are used to get derivatives at grid points. • Do some reading on these… will be important 37 for future assignments.

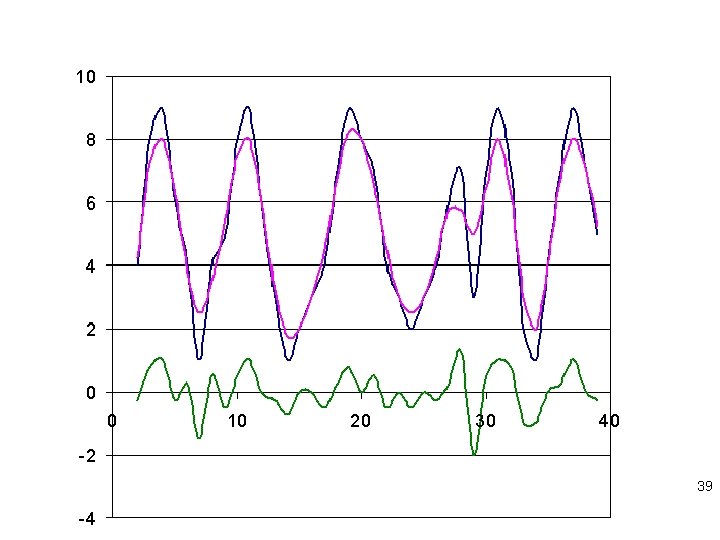
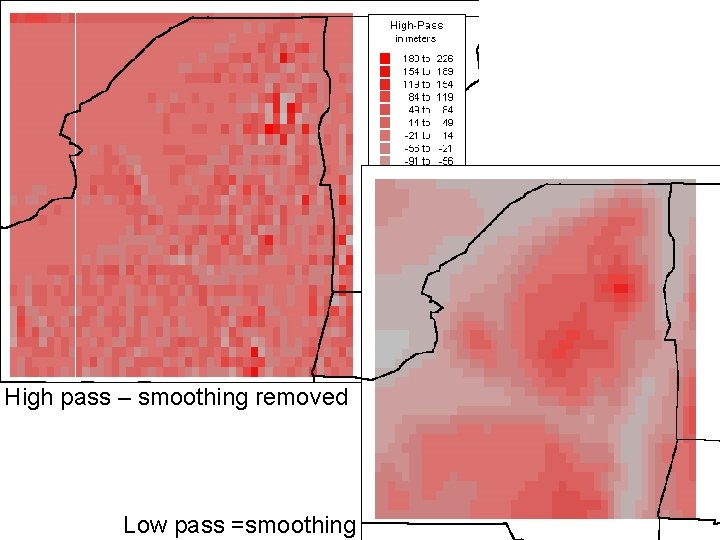
Spatial analysis of continuous fields • Filtering (Smoothing = low-pass filter) • High-pass filter is the image with the low-pass (i. e. smoothing) removed • One-dimension; V(i) = [ V(i-1) + 2 V(i) + V(i+1) ] /4 another weighted average 38

39

• Square window (convolution, moving window) • New value for V is weighted average of points within specified window. – Vij = f [ SUM k=i-m, i+m SUM l=j-n, j+n Vkl wkl ] / SUM wkl , – f = operator – w = weight 40

• Each cell can have same or different weight but typically SUM wkl = 1. For equal weighting, if n x m = 5 x 5 = 25, then each w = 1/25. • Or weighting can be specified for each cell. For example for 3 x 3 the weight array might be: 1/15 2/15 3/15 2/15 1/15 So Vij = [ Vi-1, j-1 + 2 Vi, j-1 + Vi+1, j-1 + 2 Vi-1, j + 3 Vi, j + 2 Vi+1, j +Vi-1, j+1 +2 Vi, j+1 +Vi+1, j+1 ] /15 41

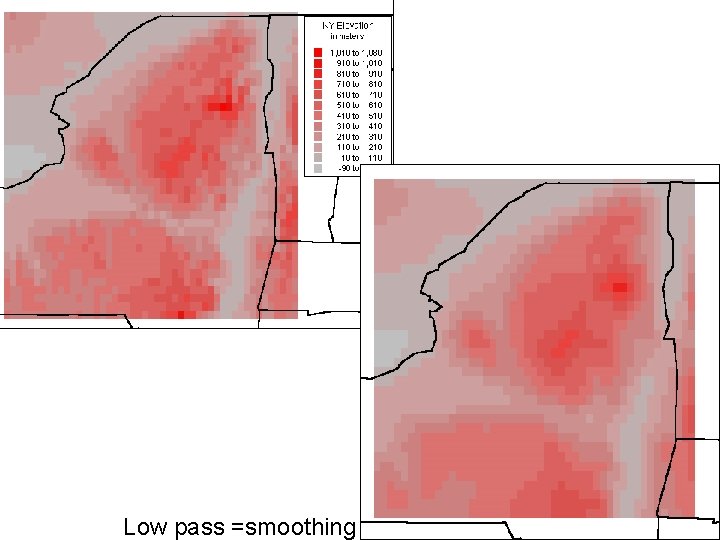
42 Low pass =smoothing

High pass – smoothing removed 43 Low pass =smoothing

Modal filters • The value or type at center cell is the most common of surrounding cells. • Example 3 x 3: • AABCADCABB • A B C A C B A C -> A A A C C C B B B • BAACBCBBBA 44

Or • You can use the minimum, maximum, or range. For example the minimum: • AABCADCABB • A B C A C B A C -> A A A A A • BAACBCBBBA – No powerpoint animation hell… • Note - Because it requires sorting the values in the window, it is a computationally intensive task, the modal filter is considerably 45 less efficient than other smoothing filters.

Median filter • Median filters can be used to emphasize the longerrange variability in an image, effectively acting to smooth the image. • This can be useful for reducing the noise in an image. The algorithm operates by calculating the median value (middle value in a sorted list) in a moving window centered on each grid cell. • The median value is not influenced by anomalously high or low values in the distribution to the extent that the average is. • As such, the median filter is far less sensitive to shot 46 noise in an image than the mean filter.

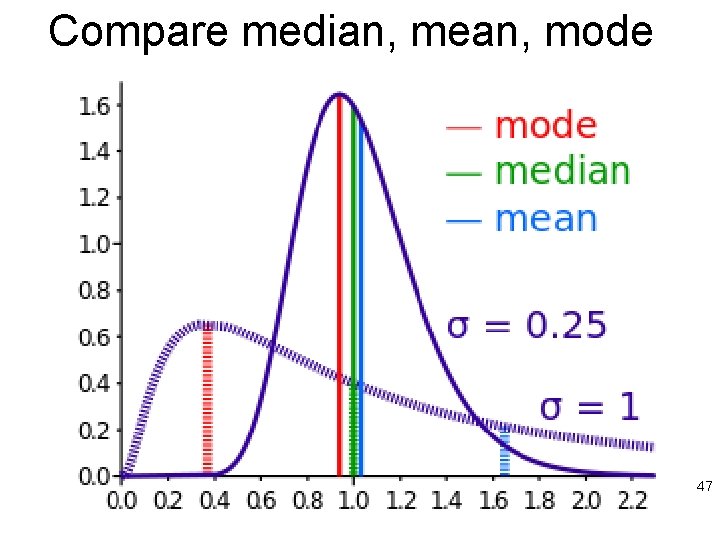
Compare median, mean, mode 47

Median filter • Because it requires sorting the values in the window, a computationally intensive task, the median filter is considerably less efficient than other smoothing filters. • This may pose a problem for large images or large neighborhoods. • Neighborhood size, or filter size, is determined by the userdefined x and y dimensions. These dimensions should be odd, positive integer values, e. g. 3, 5, 7, 9. . . • You may also define the neighborhood shape as either squared or rounded. • A rounded neighborhood approximates an ellipse; a rounded neighborhood with equal x and y dimensions approximates a 48 circle.

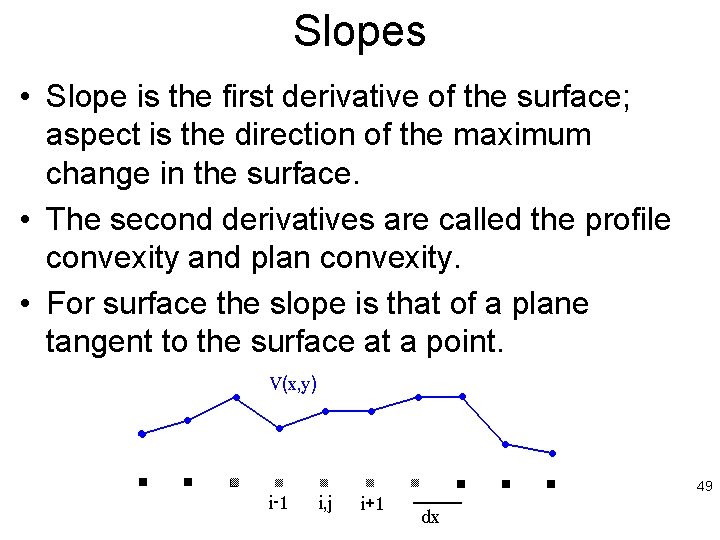
Slopes • Slope is the first derivative of the surface; aspect is the direction of the maximum change in the surface. • The second derivatives are called the profile convexity and plan convexity. • For surface the slope is that of a plane tangent to the surface at a point. 49

Gradient • The gradient, which is a vector written as del V, contains both the slope and aspect. – del V = ( d. V/dx, d. V/dy ) • For discrete data we often use finite differences to calculate the slope. • In the plot above the first derivative at Vij could be taken as the slope between points at i-1 and i+1. – d Vij / d x = ( Vi+1, j – Vi-1, j ) / (2 dx) 50

Second derivative • … is the slope of the slope. We take the change in slope between i+1 and i, and between i and i-1. d 2 V / dx 2 = [ ( Vi+1, j – Vi, j ) / dx - ( Vi, j – Vi-1, j ) / dx ] / dx • The slope, which is the magnitude of del V, is: | del V | = [ (d V / d x )2 + ( d V / d y )2 ]1/2 51

End of Part I 52

Summary • Purpose of analysis should drive the type that is conducted • Many constraints due to prior management of the data • Become proficient in a variety of methods, tools 53

Reading • Reading this week, will span module 7 (Data Analysis II) • No reading discussion for Module 5 or 6 • Note reading for module 7 – possible data sources for project definitions – There is a lot of material to review before module 7 • Module 7 defines the group projects, so come familiar with the data out there! • Working with someone else's data 54

Practical details for module 5 • The preparation for collection is Assignment 1 (plan) which is theoretical exercise • Module 5 will be to see how much of this plan translates into practice • Ground rules – You must attend the start of class – Do ONE of your data collections during this module – No one off collections, i. e. must be something you could repeat – This is an individual exercise, you will see what 55 others have done in module 6 presentations

Practical details for module 5 • A write up is required, details in Assignment 2 • No “analysis” is required but you will need to present your data (module 6) so interpretation may be required • Sources? ? – Images – Sound – Existing devices, sensors – Others? 56

Data Collection Minimums • 100 data points or more • Think 15 % more • Is too many too much? – Subset your data – Remember provenance • Don’t forget references! 57