CYCLIC CONFIGURATIONS AND HAAR GRAPHS Haar graph of

CYCLIC CONFIGURATIONS AND HAAR GRAPHS

Haar graph of a natural number Let us write n in binary: n = bk-12 k-1 + bk-2 2 k-2 +. . . + b 12 + b 0 where B(n) = (bk-1, bk-2, . . . , b 1, b 0), bk-1= 1 are binary digits of n. Graph H(n) = H(k; n) that is called the Haar graph of natural number n, has vertex set ui, vi, i=0, 1, . . . , k-1. Vertex ui is adjacent to vi+j, if and only if bj = 1 (arithmetic is mod k).

Remark When defininig H(n) we assumed that k is the number of binary digits of n. In general for H(k; n) one can take k to be greater than the number of binary digits. In such a case a different graph is obtained!

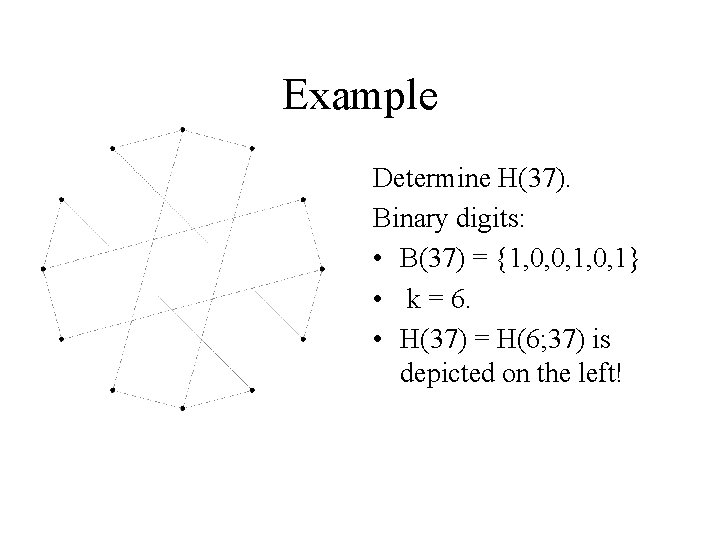
Example Determine H(37). Binary digits: • B(37) = {1, 0, 0, 1} • k = 6. • H(37) = H(6; 37) is depicted on the left!

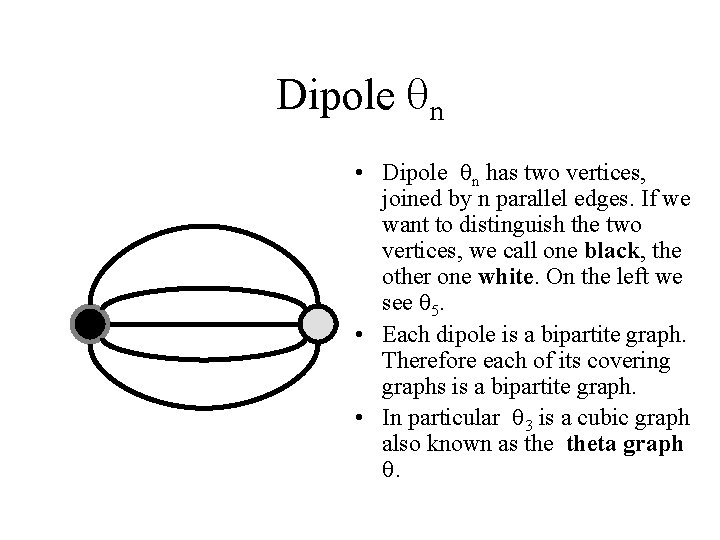
Dipole qn • Dipole qn has two vertices, joined by n parallel edges. If we want to distinguish the two vertices, we call one black, the other one white. On the left we see q 5. • Each dipole is a bipartite graph. Therefore each of its covering graphs is a bipartite graph. • In particular q 3 is a cubic graph also known as theta graph q.

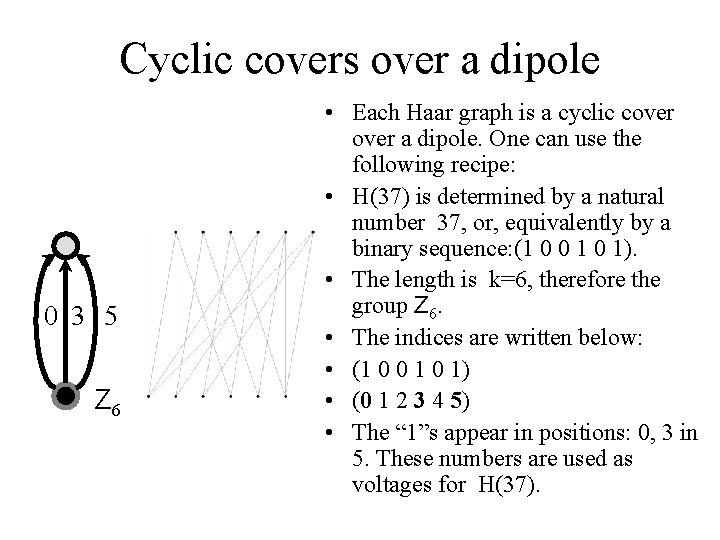
Cyclic covers over a dipole 0 3 5 Z 6 • Each Haar graph is a cyclic cover a dipole. One can use the following recipe: • H(37) is determined by a natural number 37, or, equivalently by a binary sequence: (1 0 0 1). • The length is k=6, therefore the group Z 6. • The indices are written below: • (1 0 0 1) • (0 1 2 3 4 5) • The “ 1”s appear in positions: 0, 3 in 5. These numbers are used as voltages for H(37).

Exercises • Graph on the left is the socalled Heawood graph H. Prove: – H is bipartite – H is a Haar graph. (Find n!) – Determine H as a cyclic cover q 3. . – Prove that H has no cycle of length < 6. – Prove that H is the smallest cubic graph of girth 6. – Find a hexagonal embedding of H in torus. – Determine the dual of the embedded H.

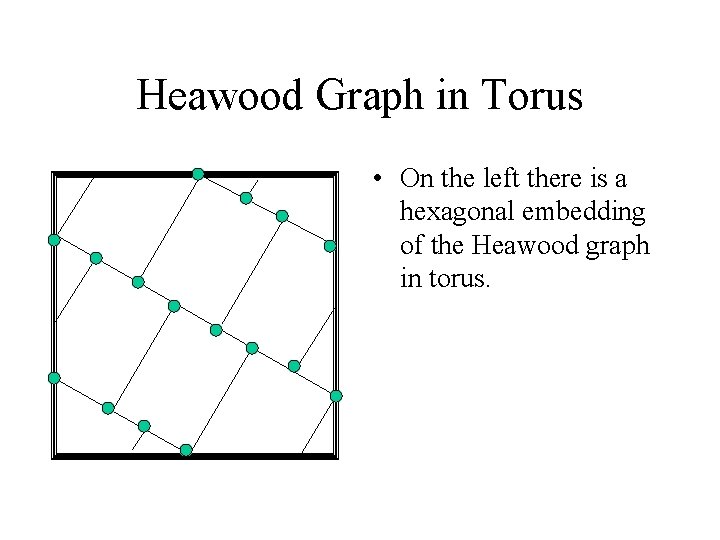
Heawood Graph in Torus • On the left there is a hexagonal embedding of the Heawood graph in torus.

Connected Haar graphs • Graph G is connected if there is a path between aby two of its vertices. • There exist disconnected Haar graphs, for instance H(10). • Define n to be connected, if the corresponding Haar graph H(n) is connected. • Disconnected numbers: 2, 4, 8, 10, 16, 32, 34, 36, 40, 42, 64. . .

Exercises • Prove that each 2 m is a disconnected number. • Show that the Möbius-Kantor graph G(8, 3) is a Haar graph of some number. Which number is that? • (*) Determine all generalized Petersen graphs that are Haar graphs of some natural number. • Show that some Haar graphs are circulants. • Show that some Haar graphs are non-circulants.

Exercises, Continuation • Prove that each Haar graph is vertex transitive. • Prove that each Haar graph is a Cayley graph for a dihedral group. • Prove that there exist bipartite Cayley graphs of dihedral groups that are not Haar graphs (such as the graph on the left).

Exercises, The End • The numbers n and m are cyclically equivalent, if the binary string of the first number can be cyclically transformed to the binary string of the second number. This means that the string can be cyclically permuted, mirrored or multiplied by a number relatively prime with the string length. • The numbers n and m are Haar equivalent, if their Haar graphs are isomorphic: H(n) = H(m). • Prove that cyclic equivalence implies Haar equivalence. • Determine all numbers that are cyclically equivalent to 69. • Use computer to show that 137331 and 143559 are Haar ekquivalent, but are not cyclically equivalent.

The Mark Watkins Graph • Cubic Haar graph H(536870930) has an interesting property. 536870930 is the smallest connected number that is cyclically equivalent to no odd number. • Show that each Haar graph of an odd number H(2 n+1) is hamiltonian and therefore connected.

Girth of Connected Haar graphs • K 2 is the only connected 1 -valent Haar graph. • Even cycles C 2 n are connected 2 -valent Haar graphs. • Theorem: Let H be a connected Haar graph of valence d > 2. Then either girth(H) = 4 or girth(H) = 6.

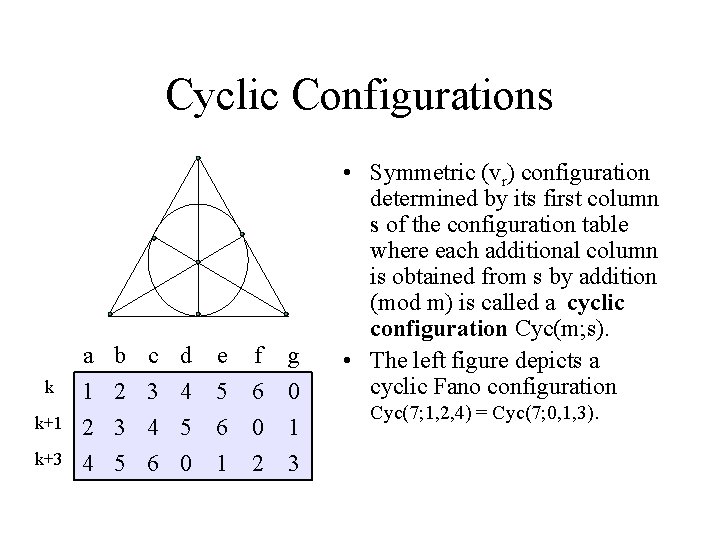
Cyclic Configurations k k+1 k+3 a 1 2 4 b 2 3 5 c 3 4 6 d 4 5 0 e 5 6 1 f 6 0 2 g 0 1 3 • Symmetric (vr) configuration determined by its first column s of the configuration table where each additional column is obtained from s by addition (mod m) is called a cyclic configuration Cyc(m; s). • The left figure depicts a cyclic Fano configuration Cyc(7; 1, 2, 4) = Cyc(7; 0, 1, 3).

Connection to Haar graphs • Theorem: Symmetric configuration (vr), r ¸ 1 is cyclic, if and only if its Levi graph is a Haar graph with girth ¹ 4. • Corollary: Each cyclic configuration is point- and line-transitive and combinatorially self-dual. • Corollary: Each cyclic configuration (vr), r > 2 contains a triangle. • Question: Does there exist a cyclic configuration that is not combinatorially self-polar?

Problem • Study cyclic configurations with respect to flag orbits.