Curvas curiosas Cicloide Cardioide Espiral de Arqumedes Lemniscata






- Slides: 14

Curvas curiosas Cicloide Cardioide Espiral de Arquímedes Lemniscata Bruja de Agnesi Astroide 1

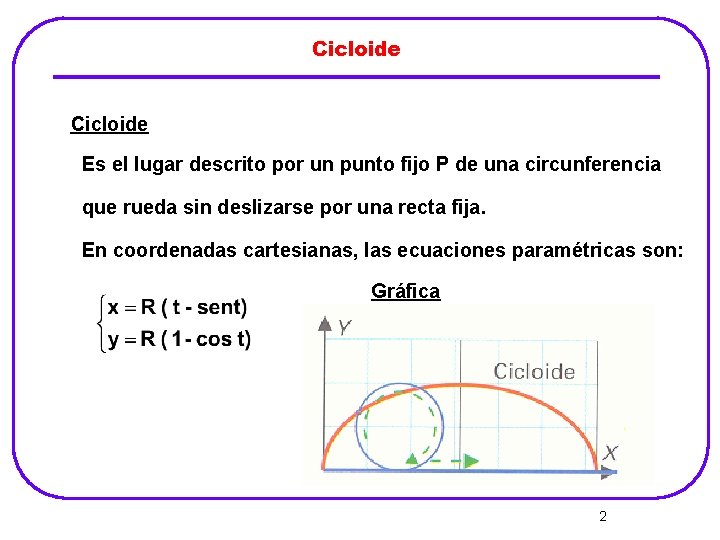
Cicloide Es el lugar descrito por un punto fijo P de una circunferencia que rueda sin deslizarse por una recta fija. En coordenadas cartesianas, las ecuaciones paramétricas son: Gráfica 2

Cicloide l l Problema propuesto por Johan BERNOULLI (1696) Entre todas las curvas que unen dos puntos del plano la curva de descenso más rápido (braquistócrona) es la cicloide. Un ejemplo de arco de cicloide son las pistas de salto de esquí. Es tautocrona: si invertimos una cicloide y dejamos caer rodando dos canicas a diferente altura (sin rozamiento), las dos llegarán al punto más bajo al mismo tiempo. Es isócrona: el período de un péndulo no varia cuando este oscila entre dos cicloides, siendo la trayectoria otra cicloide. 3

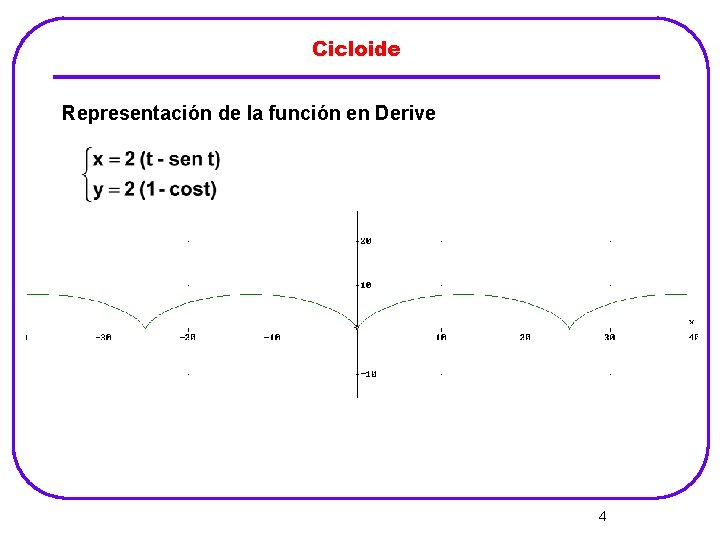
Cicloide Representación de la función en Derive 4

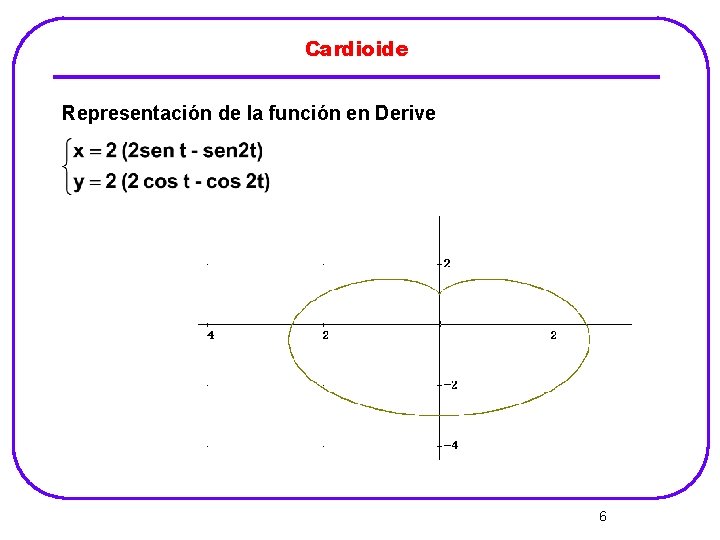
Cardioide Es el lugar descrito por un punto fijo P de una circunferencia que rueda sin deslizarse sobre otra circunferencia que tiene el mismo radio. Las ecuaciones paramétricas, en coordenadas cartesianas, son: 5

Cardioide Representación de la función en Derive 6

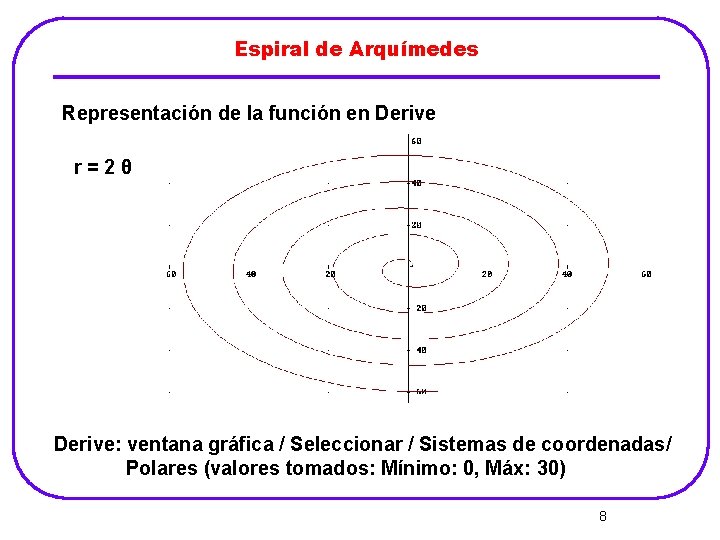
Espiral de Arquímedes Es una espiral que conserva la misma distancia entre las espiras La ecuación explícita, en polares, es: r = k θ 7

Espiral de Arquímedes Representación de la función en Derive r=2θ Derive: ventana gráfica / Seleccionar / Sistemas de coordenadas/ Polares (valores tomados: Mínimo: 0, Máx: 30) 8

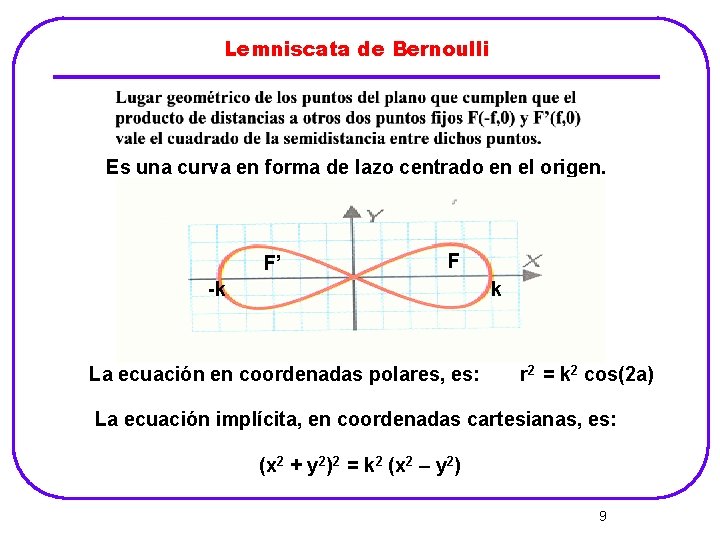
Lemniscata de Bernoulli Es una curva en forma de lazo centrado en el origen. F’ F -k k La ecuación en coordenadas polares, es: r 2 = k 2 cos(2 a) La ecuación implícita, en coordenadas cartesianas, es: (x 2 + y 2)2 = k 2 (x 2 – y 2) 9

Lemniscata de Bernouilli Representación de la función en Derive (x 2 + y 2)2 = 22 (x 2 – y 2) Nota: Para representar en Derive funciones en forma implícita es conveniente pasar a explícita (lupa) 10

Bruja de Agnesi Esta curva se conocía como la versiera, significa “dar vueltas” En la traducción al inglés, esta palabra fue confundida con aversiera que significa “esposa del diablo” y así paso al castellano como “bruja”. La ecuación implícita, en coordenadas cartesianas, es: y=a 3/(x 2+a 2) 11

Bruja de Agnesi Representación de la función en Derive y=a 3/(x 2+a 2) Nota: Para representar en Derive hay que dar un valor a la constante a. 12

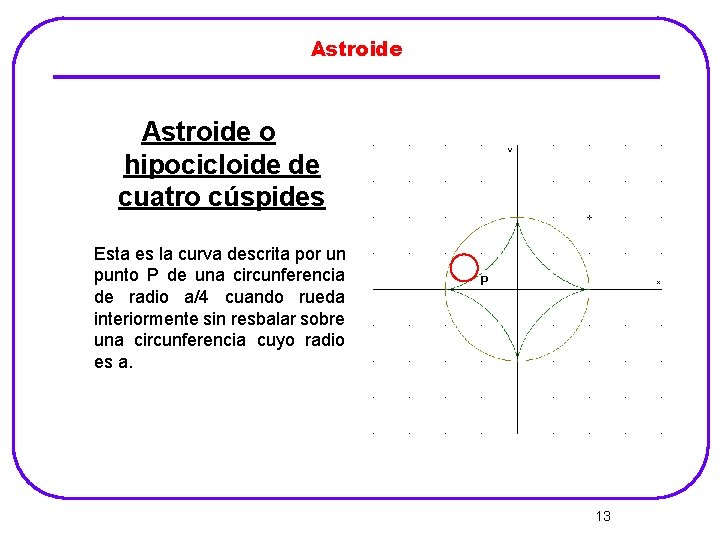
Astroide o hipocicloide de cuatro cúspides Esta es la curva descrita por un punto P de una circunferencia de radio a/4 cuando rueda interiormente sin resbalar sobre una circunferencia cuyo radio es a. P 13

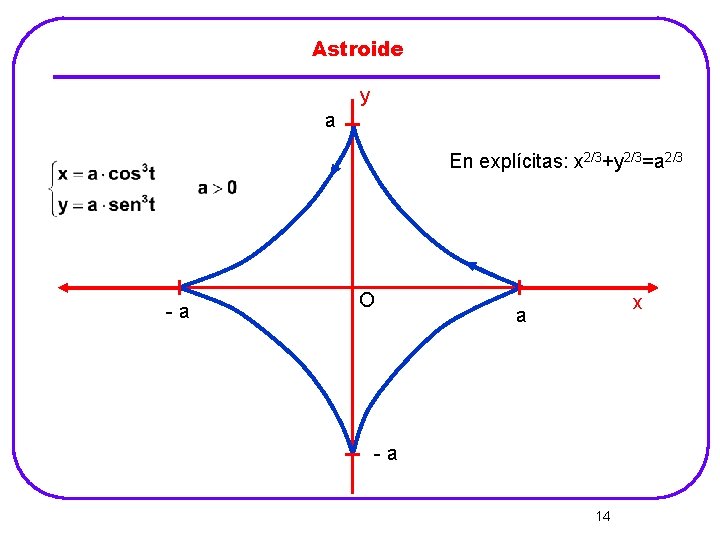
Astroide y a En explícitas: x 2/3+y 2/3=a 2/3 -a O x a -a 14
 Folium di cartesio
Folium di cartesio Cicloide ejercicios resueltos
Cicloide ejercicios resueltos Fis
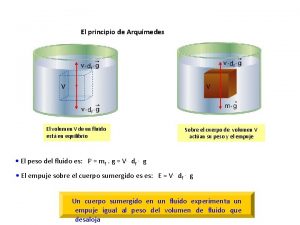
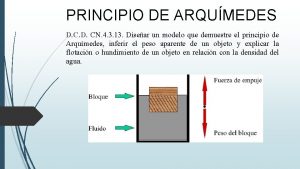
Fis Aplicaciones del principio de arquímedes.
Aplicaciones del principio de arquímedes. Arqumedes
Arqumedes Arqumedes
Arqumedes Curva de flujo volumen
Curva de flujo volumen Reação exergônica
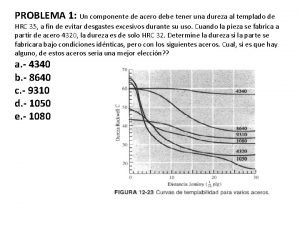
Reação exergônica Curvas de templabilidad
Curvas de templabilidad Tipos de curvas en el espacio
Tipos de curvas en el espacio Lineas tirantes
Lineas tirantes Curvas de indiferencia atipicas
Curvas de indiferencia atipicas Cuerpos cetonicos
Cuerpos cetonicos Curva de capabilidad
Curva de capabilidad Naturaleza numero de oro
Naturaleza numero de oro