CSE 20 DISCRETE MATH Prof Shachar Lovett http

CSE 20 DISCRETE MATH Prof. Shachar Lovett http: //cseweb. ucsd. edu/classes/wi 15/cse 20 -a/ Clicker frequency: CA

Todays topics • Countably infinitely large sets • Uncountable sets • “To infinity, and beyond!” (really, we’re going to go beyond infinity)

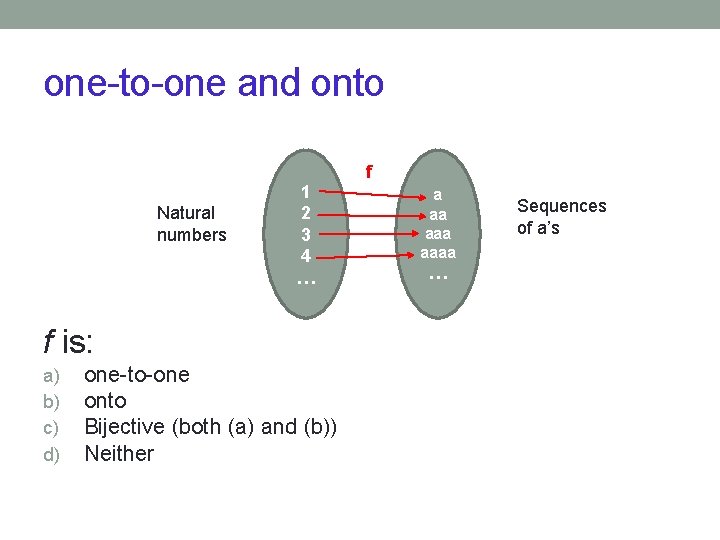
Set Theory and Sizes of Sets • How can we say that two sets are the same size? • Easy for finite sets (count them)--what about infinite sets? • Georg Cantor (1845 -1918), who invented Set Theory, proposed a way of comparing the sizes of two sets that does not involve counting how many things are in each • Works for both finite and infinite • SET SIZE EQUALITY: • Two sets are the same size if there is a bijective (one-to-one and onto) function mapping from one to the other • Intuition: neither set has any element “left over” in the mapping

one-to-one and onto Natural numbers 1 2 3 4 … f is: a) b) c) d) one-to-one onto Bijective (both (a) and (b)) Neither f a aa aaaa … Sequences of a’s

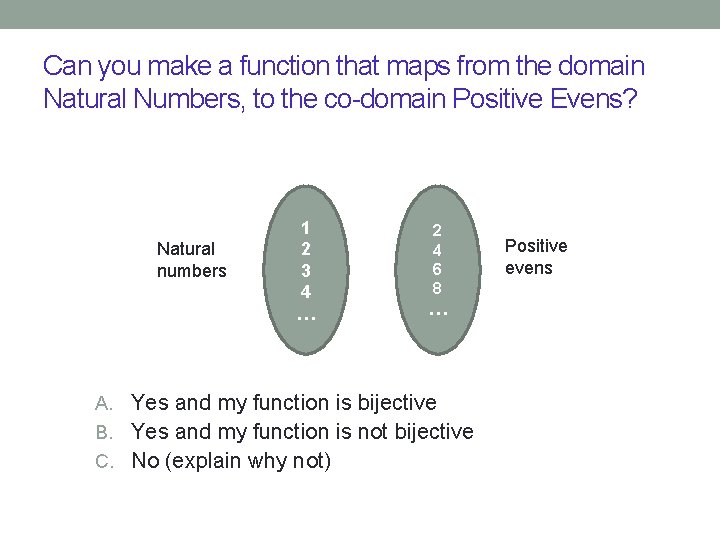
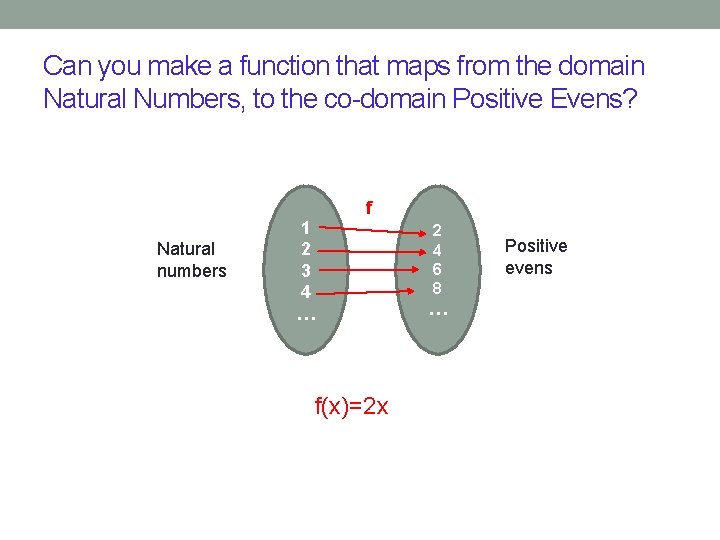
Can you make a function that maps from the domain Natural Numbers, to the co-domain Positive Evens? Natural numbers 1 2 3 4 … 2 4 6 8 … A. Yes and my function is bijective B. Yes and my function is not bijective C. No (explain why not) Positive evens

Can you make a function that maps from the domain Natural Numbers, to the co-domain Positive Evens? Natural numbers 1 2 3 4 … f f(x)=2 x 2 4 6 8 … Positive evens

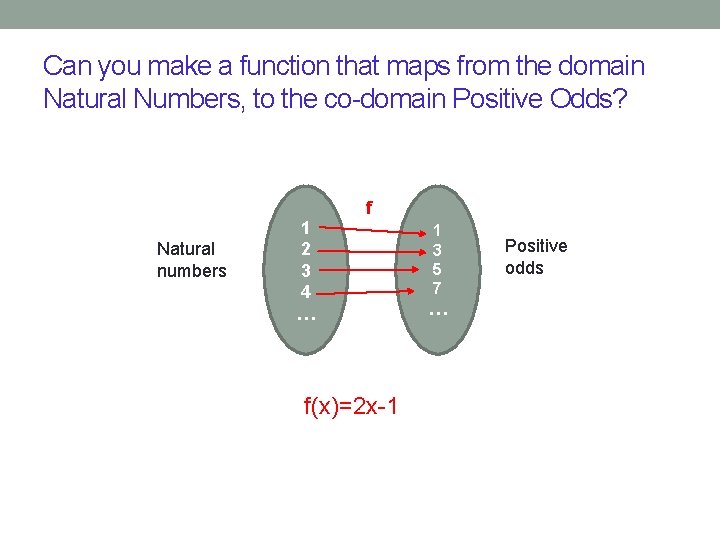
Can you make a function that maps from the domain Natural Numbers, to the co-domain Positive Odds? Natural numbers 1 2 3 4 … 1 3 5 7 … A. Yes and my function is bijective B. Yes and my function is not bijective C. No (explain why not) Positive odds

Can you make a function that maps from the domain Natural Numbers, to the co-domain Positive Odds? Natural numbers 1 2 3 4 … f f(x)=2 x-1 1 3 5 7 … Positive odds

Countably infinite size sets • So |N| = |Even|, even though it seems like it should be |N| = 2|Even| • Also, |N| = |Odd| • Another way of thinking about this is that two times infinity is still infinity • Does that mean that all infinite size sets are of equal size?

It gets even weirder: Rational Numbers (for simplicity we’ll do ratios of natural numbers, but the same is true for all Q) • 1/1 1/2 1/3 1/4 1/5 1/6 … 2/1 2/2 2/3 2/4 2/5 2/6 … 3/1 3/2 3/3 3/4 3/5 3/6 … 4/1 4/2 4/3 4/4 4/5 4/6 … 5/1 5/2 5/3 5/4 5/5 5/6 . . . 6/1 6/2 6/3 6/4 6/5 6/6 … … … …

It gets even weirder: Rational Numbers (for simplicity we’ll do ratios of natural numbers, but the same is true for all Q) • 1/1 1/2 1/3 1/4 1/5 1/6 2/1 2/2 2/3 2/4 2/5 2/6 3/1 3/2 3/3 3/4 3/5 3/6 4/1 4/2 4/3 4/4 4/5 4/6 5/1 5/2 5/3 5/4 5/5 5/6 6/1 6/2 6/3 6/4 6/5 6/6 … … … Is… there a bijection from … the natural … numbers to …Q+? . . . A. Yes B. No …

It gets even weirder: Rational Numbers (for simplicity we’ll do ratios of natural numbers, but the same is true for all Q) • 1/1 1 1/2 2 1/3 4 1/4 6 1/5 10 1/6 … 2/1 3 2/2 x 2/3 7 2/4 x 2/5 2/6 … 3/1 5 3/2 8 3/3 x 3/4 3/5 3/6 … 4/1 9 4/2 x 4/3 4/4 4/5 4/6 … 5/1 11 5/2 5/3 5/4 5/5 5/6 . . . 6/1 6/2 6/3 6/4 6/5 6/6 … … … …

Sizes of Infinite Sets • The number of Natural Numbers is equal to the number of positive Even Numbers, even though one is a proper subset of the other! • |N| = |E+|, not |N| = 2|E+| • The number of Rational Numbers is equal to the number of Natural Numbers • |N| = |Q+|, not |Q+| ≈ |N|2 • But it gets even weirder than that: • It might seem like Cantor’s definition of “same size” for sets is overly broad, so that any two sets of infinite size could be proven to be the “same size” • Actually, this is not so

Not all infinite sets have the same size •

Thm. |[0, 1]| != |N| Proof by contradiction: Assume |[0, 1]| = |N|, so a bijective function f exists between N and [0, 1]. Natural numbers 1 2 3 4 … f ? ? ? z ? … Real numbers in [0, 1]

Thm. |[0, 1]| != |N| Proof by contradiction: Assume |[0, 1]| = |N|, so a bijective function f exists between N and [0, 1]. n f(n) 1 . 100000… 2 . 333333… 3 . 314159… … … What is x in this example? a). 244… b). 134… c). 031… d). 245…

Thm. |[0, 1]| != |N| Proof by contradiction: Assume |[0, 1]| = |N|, so a bijective function f exists between N and [0, 1]. n f(n) 1 . d 11 d 12 d 13 d 14… 2 . d 21 d 22 d 23 d 24… 3 . d 31 d 32 d 33 d 34… … … What is x? a). d 11 d 12 d 13… b). d 11 d 22 d 33 … c). [d 11+1] [d 22+1] [d 33+1] … d). [d 11+1] [d 21+1] [d 31+1] …

Thm. |[0, 1]| != |N| Proof by contradiction: Assume |[0, 1]| = |N|, so a bijective function f exists between N and [0, 1]. • How do we reach a contradiction? • Must show that x cannot be f(n) for any n • How do we know that x ≠ f(n) for any n? n f(n) 1 . d 11 d 12 d 13 d 14… 2 . d 21 d 22 d 23 d 24… 3 . d 31 d 32 d 33 d 34… … … a) We can’t know if x = f(n) without knowing what f is and what n is b) Because x’s nth digit differs from n‘s nth digit c) Because x’s nth digit differs from f(n)’s nth digit

Diagonalization n f(n) 1 . d 11 d 12 d 13 d 14 d 15 d 16 d 17 d 18 d 19… 2 . d 21 d 22 d 23 d 24 d 25 d 26 d 27 d 28 d 29… 3 . d 31 d 32 d 33 d 34 d 35 d 36 d 37 d 38 d 39… 4 . d 41 d 42 d 43 d 44 d 45 d 46 d 47 d 48 d 49… 5 . d 51 d 52 d 53 d 54 d 55 d 56 d 57 d 58 d 59… 6 . d 61 d 62 d 63 d 64 d 65 d 66 d 67 d 68 d 69… 7 . d 71 d 72 d 73 d 74 d 75 d 76 d 77 d 78 d 79… 8 . d 81 d 82 d 83 d 84 d 85 d 86 d 87 d 88 d 89… 9 . d 91 d 92 d 93 d 94 d 95 d 96 d 97 d 98 d 99… … … 20

Some infinities are more infinite than other infinities • Natural numbers are called countable • • • Real numbers are uncountable • • Any set that can be put in correspondence with N is called countable (ex: E+, ℚ+). Equivalently, any set whose elements can be enumerated in an (infinite) sequence a 1, a 2, a 3, … Any set for which cannot be enumerated by a sequence a 1, a 2, a 3, … is called “uncountable” But it gets even weirder… • There are more than two categories!

Some infinities are more infinite than other infinities |N| is called א 0 o |E+| = |Q| = א 0 |[0, 1]| is maybe א 1 o o Although we just proved that |N| < |[0, 1]|, and nobody has ever found a different infinity between |N| and |[0, 1]|, mathematicians haven’t proved that there are not other infinities between |N| and |[0, 1]|, making |[0, 1]| = א 2 or greater In fact, it can be proved that such theorems can never be proven… Sets exist whose size is א 0, א 1, א 2, א 3… An infinite number of aleph numbers! o An infinite number of different infinities

Famous People: Georg Cantor (1845 -1918) • His theory of set size, in particular transfinite numbers (different infinities) was so strange that many of his contemporaries hated it • Just like many CSE 20 students! • “scientific charlatan” “renegade” “corrupter of youth” • “utter nonsense” “laughable” “wrong” • “disease” • “I see it, but I don't believe it!” –Georg Cantor himself “The finest product of mathematical genius and one of the supreme achievements of purely intellectual human activity. ” –David Hilbert

Next class • Final review