CRYPTOGRAPHY AND THE MATH MAJOR Dr Mihai Caragiu

CRYPTOGRAPHY AND THE MATH MAJOR Dr. Mihai Caragiu Mathematics Department Ohio Northern University

Cryptography: the art or science of transforming an intelligible message into one that is unintelligible, and then retransforming that message back to its original form…

Mathematics plays a crucial role in cryptography!

2000 years ago Julius Caesar used a simple substitution cipher (replace each letter of message by a letter a fixed distance – k – away) Say, for example, k = 3. Then SCIENCE transforms into: VFLHQFH This is not a secure cryptosystem! Still, there is some mathematics hidden here which is indeed very useful for the design of more reliable cryptosystems…

MODULAR ARITHMETIC First let us associate numbers from 0 through 25 to the twenty six letters of the English alphabet: A 0 B 1 C 2 D 3 E 4 … X 23 Y 24 Z 25 Now, let us learn how to compute “modulo 26”. This means computing within a “universe” in which the only available numbers are those from 0 through 25: U = {0, 1, 2, …, 25}

U = {0, 1, 2, …, 25} What about the other numbers? 26, 27, … Well, 26 is 0 in disguise! 27 is 1 in disguise! … 531 is 11 in disguise! – 17 is 9 in disguise! To “see” the “real face” of an integer modulo 26, divide it by 26 and take the remainder. What about 2001? 2001 = 26 · 76 + 25 Technically we denote this by 2001 (mod 26) = 25 Therefore 2002 will be simply… 0 (modulo 26) !

How to add mod 26, then? Well, add as usual, then take the remainder! 17 + 15 = 6 22 + 18 = 14 … How to multiply? Multiply as usual, then take the remainder! 15 · 17 = 21 11 · 5 = 3 … Caesar’s cipher in modular arithmetic: X X + 3 (mod 26) Decryption: X X – 3 (mod 26)

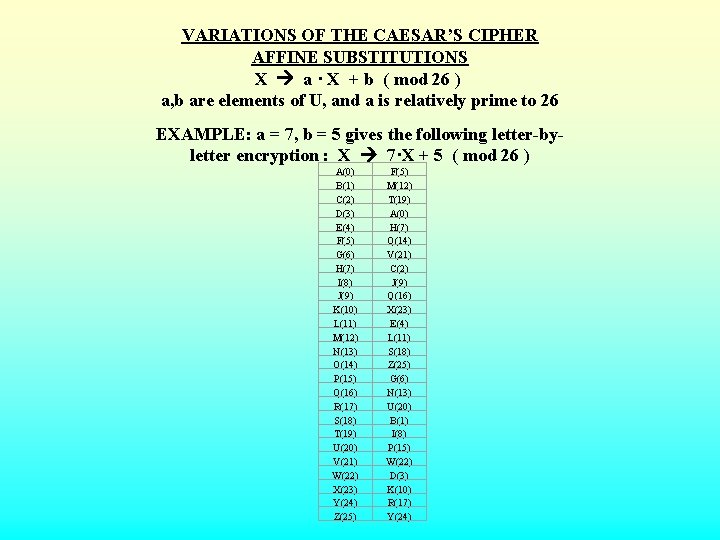
VARIATIONS OF THE CAESAR’S CIPHER AFFINE SUBSTITUTIONS X a · X + b ( mod 26 ) a, b are elements of U, and a is relatively prime to 26 EXAMPLE: a = 7, b = 5 gives the following letter-byletter encryption : X 7·X + 5 ( mod 26 ) A(0) B(1) C(2) D(3) E(4) F(5) G(6) H(7) I(8) J(9) K(10) L(11) M(12) N(13) O(14) P(15) Q(16) R(17) S(18) T(19) U(20) V(21) W(22) X(23) Y(24) Z(25) F(5) M(12) T(19) A(0) H(7) Q(14) V(21) C(2) J(9) Q(16) X(23) E(4) L(11) S(18) Z(25) G(6) N(13) U(20) B(1) I(8) P(15) W(22) D(3) K(10) R(17) Y(24)

INVERTING THE AFFINE CIPHER X 7·X + 5 ( mod 26 ) (encryption formula) THE “INVERSE TRANSFORMATION” X 15·X + 3 (mod 26) (decryption formula) EXAMPLE Say, by using the encryption formula Alice encrypts “ 11” into 7· 11 + 5 = 4 ( mod 26 ) and sends “ 4” over to Bob… Bob gets the “ 4” and wants to decrypt it by using the decryption formula. He computes: 4· 15 + 3 = 63 = 52 + 11 = 11 (mod 26) and thus he recovers the “ 11”.

UNFORTUNATELY, letter-by-letter encryption is easy to break (for example, by using a frequency analysis) EXAMPLE: Assume a smart eavesdropper Q suspects that Alice and Bob use an encryption of the type described above, that is, X a·X+b (mod 26). But Q does not know the values of a and b. Well, Q keeps listening, and after a few moments realizes that the letter that has the highest frequency in the (otherwise unintelligible) cyphertext that Alice is sending over is H (7). Moreover, Q realizes that the letter coming next in the order of frequency is I (8). At this moment Q quickly opens a linguistics book and finds out that the letters having the two highest frequencies in English are E (4) (highest) and T (19) (second highest frequency). Finding a and b is not difficult: indeed, the encryption of 4 must be 7 and the encryption of 19 must be 8: a· 4+b =7 (mod 26) a· 19+b =8 (mod 26) This is a system of two equations with two unknowns (in modular arithmetic though), which is not difficult to solve.

a· 4+b =7 (mod 26) a· 19+b =8 (mod 26) Substract the first equation out of the second to get 15·a = 1 (mod 26) from where a follows to be 7 [just check: 15· 7=105 = 26· 4+1=1 (mod 26); as a math major you will find out efficient ways of solving such equations of degree one in modular arithmetic). Once we know a=7, replace this value back into one of the two equations and you will find b=7 – a· 4= 7 – 7· 4 = – 21 = 5 (mod 26).

TOPICS CRUCIAL TO CRYPTOGRAPHY A MATH MAJOR WILL GET TO KNOW: BBasic modular arithmetic. v PPrime numbers and factoring large integers. v AAlgorithms in number theory. v AAlgebra of matrices and polynomials.