Computer Graphics Fall 2003 COMS 4160 Lecture 10

Computer Graphics (Fall 2003) COMS 4160, Lecture 10: Curves 1 Ravi Ramamoorthi http: //www. cs. columbia. edu/~cs 4160

Curves: Motivation • • Key for modeling in computer graphics Interpolation of data Surfaces are (simple) extension Modeling of shape

History Approximating/Interpolating set of points – From auto manufacturing (Pierre Bezier: Renault) “In France, at that time, very little was known about the work performed in the American aircraft industry; the papers from James Ferguson were not much displayed before 1964; Citroen was very secretive about the results obtained by Paul de Casteljau, and the famous technical report MAC-TR 41 (by S. A. Coons) did not appear before 1967; The works of W. Gordon and R. Risenfeld were printed in 1974. ” “When it was suggested that these curves could replace sweeps and french curves, most stylists objected that they had invented their own templates and would not change. It was solemnly promised that their “secret” curves would be translated in secret listings, and buried in the most secret part of the memory of the computer, and that nobody but they would keep the key of the vaulted cellar. In fact, the standard curves were flexible enough, and secret curves were soon forgotten. Designers and draftsmen easily understood the polygons and their relation with the shape of the corresponding curves. ”

History Approximating/Interpolating set of points – From auto manufacturing (Pierre Bezier) – General field of approximation theory – Much research in CAD, CAGD, graphics etc. – Splines: thin wood or metal strip used in construction

Outline • • • Issues in representation Bezier De Casteljau algorithm Polar forms (next time) B-Spline cubics (next time)

Representation Issues • Parametric/Implicit? [We use polynomials] • Order/Degree vs continuity (number of pieces? ) – We use low order polynomials (usually cubic) • • Interpolating vs approximating Level of continuity Convex Hull Number of parameters Invariance (Euclidean, affine, reparam, …) Local control Variational optimality

Bezier curves • • Interpolates end control points Tangents at end points P 0, P 3 are P 0 P 1, P 2 P 3 Degree = Order (# control points) – 1 Outline – – – de. Casteljau algorithm (linear, quadratic, cubic) Explicit forms: Bernstein Bezier Basis Interpretation as linear combination of basis functions 4 x 4 matrix for cubics Polar Forms

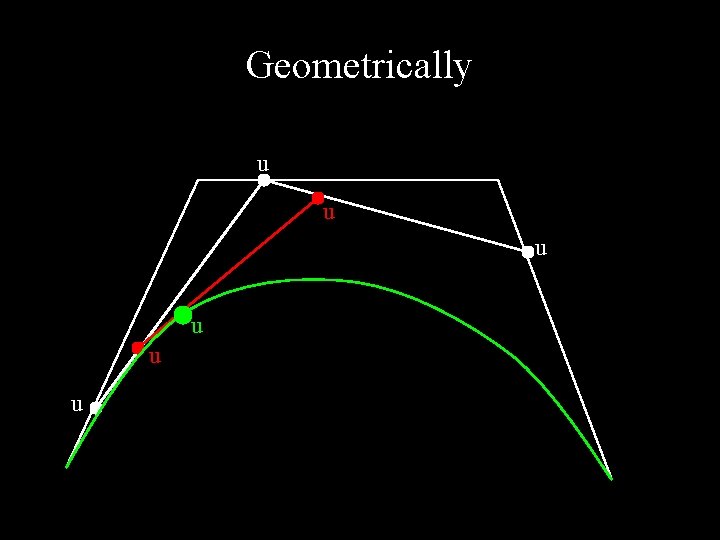
de. Casteljau Algorithm P 1 P 0 Linear Degree 1, Order 2 F(0) = P 0, F(1) = P 1 P 0 1 -u P 1 u F(u) = (1 -u) P 0 + u P 1 P 0 P 1 P 2 Quadratic Degree 2, Order 3 F(0) = P 0, F(1) = P 2 P 0 P 1 1 -u u 1 -u P 2 u u F(u) = (1 -u)2 P 0 + 2 u(1 -u) P 1 + u 2 P 0 P 2 Cubic Degree 3, Order 4 F(0) = P 0, F(1) = P 3 P 0 P 1 P 2 P 3 1 -u u 1 -u u u F(u) = (1 -u)3 P 0 +3 u(1 -u)2 P 1 +3 u 2(1 -u) P 2 + u 3 P 3

Geometrically u u u

Splines: Many Forms • Algorithmic: de. Casteljau • Explicit formulae – Linear Combination of Basis Functions – Bernstein-Bezier Polynomials – Coefficients in [(1 -u) + u]n • Matrix Form – 4 x 4 matrix for cubics – General for most splines – Bezier Formula eq [Fv. DFH 489]

Bezier curves: Properties • • • Parametric/Implicit? [Parametric] Order/Degree vs continuity (1 piece) Interpolating endpoints, approximates others Level of continuity (intrinsic C 0, achievable C 1) Convex Hull Number of parameters (4 for cubics) Invariance (Good) No Local control Variational optimality Ease of subdivision is best …