CHEM 515 Spectroscopy Lecture 9 Matrix Representation of

CHEM 515 Spectroscopy Lecture # 9 Matrix Representation of Symmetry Groups

Matrix Representations • Symmetry operators and symmetry operations can be expressed in forms of matrices. Matrices can be used as representations of symmetry operators. • A vector which is used to define a point in a space can be represented with a onedimensional matrix. row vector column vector 2

Matrices • A matrix is any rectangular array of numbers setting between two brackets. • The general form of a matrix is: or in a more compact form: A = aij The above matrix have a dimension of m×n. 3

Matrix Representations • We are concerned here with square matrices that have equal dimensions (n × n), and with column matrices for vector representations 4

Matrix Addition and Subtraction • If and only if the dimensions of the two matrices A and B are the same, they can be added or subtracted. (Both matrices have the identical amount of rows and columns) Addition can be performed by adding the corresponding elements: aij+bij 5

Matrix Addition and Subtraction 6

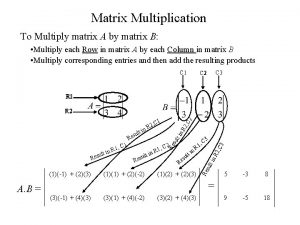
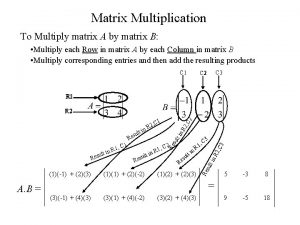
Matrix Multiplication • When the number of columns of the first matrix is the same as the number of rows in the second matrix, then matrix multiplication can be performed. 7

Matrix Multiplication 8

Matrix Multiplication • Example: 9

The Determinant of a Matrix • Determinant of a 2× 2 Matrix For the matrix: Its determinant |A| is given by: 10

The Determinant of a Matrix • Determinant of a 3× 3 Matrix For the matrix: Its determinant |A| is given by: 11

The Determinant of a Matrix • Determinant of a 3× 3 Matrix The above matrix is said to be a singular matrix. 12

Transpose of Matrices • The transpose of a matrix is found by exchanging rows for columns. For the matrix A = (aij) , its transpose is given by AT=(aji) 13

Transpose of Matrices • In the case of a square matrix (n×n), the transpose can be used to check if a matrix is symmetric. For a symmetric matrix A = AT 14

Inverse of Matrices • Assuming we have a square matrix A, which is non-singular, then there exists an n×n matrix A-1 which is called the inverse of A, such that this property holds: AA-1= A-1 A = E ; where E is the identity matrix. 15

Application of Matrices on Symmetry Operations • Matrices can be used as representations of symmetry operations. The effect of symmetry operations is going to be considered on a point defined by a column matrix: where x, y and z represent the location of that vector in space with respect to the point of origin. 16

The C 2 h Point Group as an Example • For the C 2 h symmetry, we have the elements: E, i, C 2 and σh. • Operator E (Identity) does nothing to the vector. 17

The C 2 h Point Group as an Example • The operator i can be represented by the following matrix that exchanges each coordinate into minus itself. 18

The C 2 h Point Group as an Example • The operator σh leaves x and y coordinates unchanged but inverts the sign of z. 19

The C 2 h Point Group as an Example • The operator C 2 (to be taken to set along the zaxis) changes x and y coordinates but leaves z unchanged. • It is better to derive a general matrix for an nfold rotation that is applicable for a rotation through any angle θ. 20

The C 2 h Point Group as an Example Before a rotation takes a place, the coordinates for the vector of length l is The rotated vector has coordinates From trigonometry: 21

The C 2 h Point Group as an Example Which can be expressed using matrices: For the C 2 rotation, θ = π 22

The C 2 h Point Group as an Example • The final matrix representation for C 2 rotation is: The general form of matrix representing the C 2 rotation is: 23

The Representations of the Four Operators for the C 2 h Point Group These four matrices form a mathematical group that obeys the same mathematical table for the C 2 h point group as the operations there. 24

The Representations of the Four Operators for the C 2 h Point Group C 2 h E C 2 σh i E E C 2 σh i C 2 E i σh σh σh i E C 2 i i σh C 2 E 25