Chapter 5 SCALARS VECTORS Physical Quantities All those

Chapter 5 SCALARS & VECTORS

Physical Quantities �All those quantities which can be measured are called physical quantities. Physical Quantities can be measured by means of magnitude and units.

Magnitude �A symbol which gives us the quantity of substance is called magnitude.

Unit �A symbol which gives its relation is called unit. e. g. � 5 KG 5: Magnitude Kg: Unit � 10 N 10: Magnitude N : Unit �Type of Physical Quantities: �Physical quantities are of two types. �(i) Scalar quantities (ii) Vector Quantities

SCALAR QUANTITIES �Physical quantities which can completely be specified by a number (magnitude) having an appropriate unit are known as "SCALAR QUANTITIES". �Scalar quantities do not need direction for their description. Scalar quantities are comparable only when they have the same physical dimensions. Two or more than two scalar quantities measured in the same system of units are equal if they have the same magnitude and sign. Scalar quantities are denoted by letters in ordinary type. Scalar quantities are added, subtracted, multiplied or divided by the simple rules of algebra.

EXAMPLES �Work, energy, electric flux, volume, refractive index, time, speed, electric potential, potential difference, viscosity, density, power, mass, distance, temperature, electric charge, electric flux etc

VECTORS QUANTITIES �Physical quantities having both magnitude and direction with appropriate unit are known as "VECTOR QUANTITIES". �We can't specify a vector quantity without mention of deirection. vector quantities are expressed by using bold letters with arrow sign such as: vector quantities can not be added, subtracted, multiplied or divided by the simple rules of algebra. vector quantities added, subtracted, multiplied or divided by the rules of trigonometry and geometry.

EXAMPLES �Velocity, electric field intensity, acceleration, force, momentum, torque, displacement, electric current, weight, angular momentum etc.

REPRESENTATION OF VECTORS �On paper vector quantities are represented by a straight line with arrow head pointing the direction of vector or terminal point of vector. �A vector quantity is first transformed into a suitable scale and then a line is drawn with the help of the �scale choosen in the given direction.

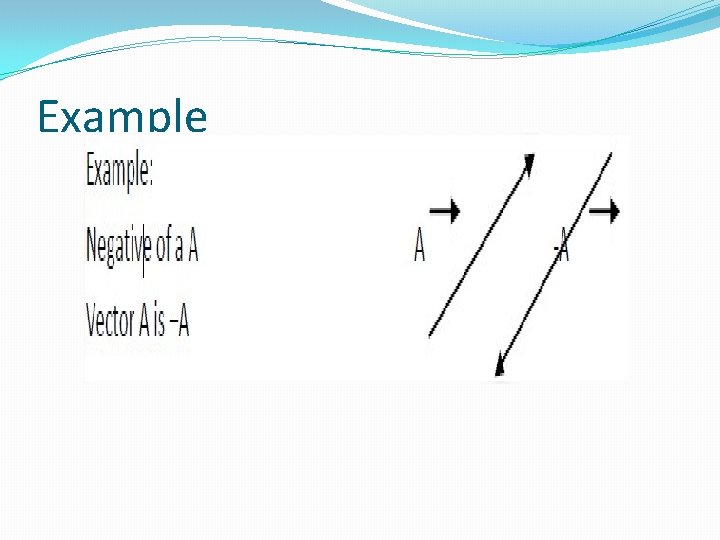
Negative vector �Negative of a vector: �Negative vector is defined as: �“A vector just equal in magnitude but exactly opposite in direction is called negative of a vector. ” �OR �“A vector having the same magnitude as that of a given vector but opposite in direction is called negative of a vector. ”

Example

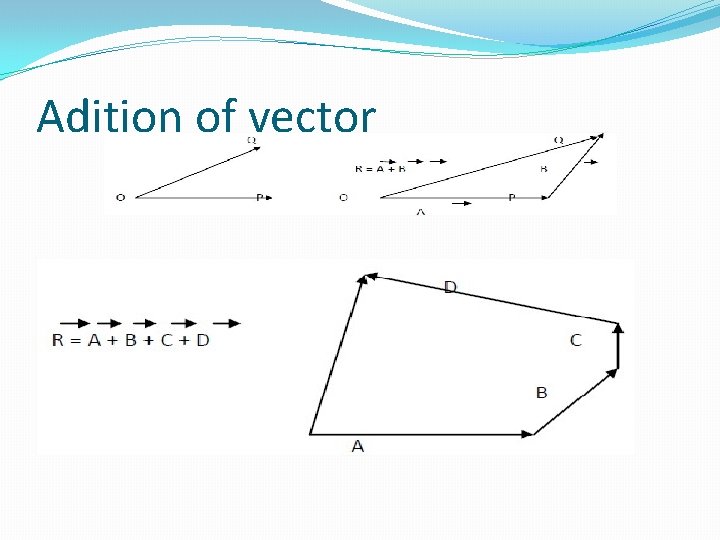
ADDITION OF VECTORS �Addition of Vectors by Head to Tail Rule: �Consider two vectors A and B represented by lines OP and OQ respectively as shown in figure we can and these two vectors by placing the tail of second vector to the head of first vector. �Now join the tail of first vector to the head of last vector, it gives us the Resultant vector as shown in Fig.

Adition of vector

Addition of vector � If more than two vectors are to be added than same method will be adopted for that. First draw the first vector than place the second vector so that its tail is at the head of First vector. Now add all the vectors just by joining the head of first vector to the tail of Next vector and in last join the tail of first vector to the head of last vector it gives us Resultant vector as shown in figure. � Resultant Vector: � “A vector which joins the tail of first vector to the head of last vector is called resultant Vector. ” � OR � “A single vector which gives the combined effect of all the vectors which are to be added is called resultant vectors. ” � It can be represented by the following equation: � R = A + B + C + ……… � Where R is the resultant vector, while A, B, C, are vectors to be added.

Subtraction of Vector �Vectors cannot be subtracted directly. They are subtracted by means of addition. To subtract vector from another vector sign of the vector is changed and then added to the other vector. For example if a vector B is to be subtracted from a Vector: A then A-B is found by adding vector A and –B.

Subtraction of vectors can be illustrated as follows

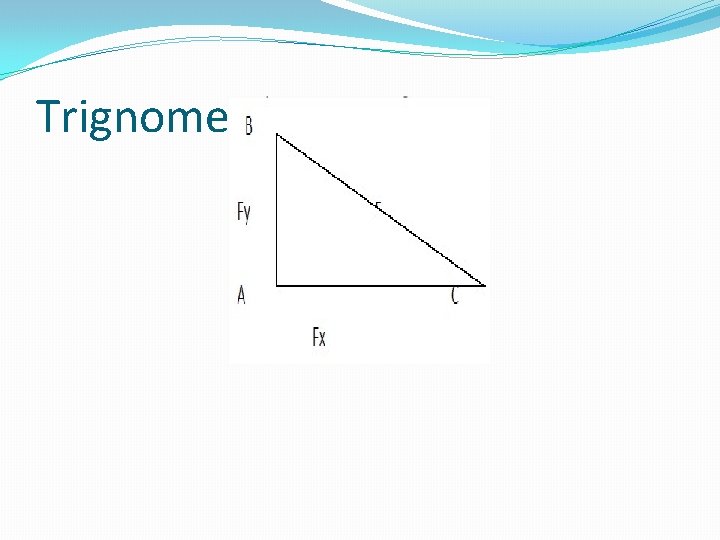
Trigonometry �Trigonometry is an important branch of mathematics and is used to solve various problems in physics. Considering the right angle triangle ABC, angle <ABC is right angle and <BAC is denoted

Trignometry � Base: (BC) Side adjacent to the angle Ø is called Base. � Perpendicular: (AB) Side opposite to the angle 0 is called Perpendicular. � Hypotenuse: (AC) Largest side or the side opposite to the right angle is called Hypotenuse � The ratios between any two sides of the right triangle represented by different names. Some of important ratios are as follows: � Sin Ø = Prep / Hyp Cosec Ø = Hyp / Perp � Cos Ø = Base / Hyp Sec Ø = Hyp / Base � Tan Ø = Perp / Base Cot Ø = Base / Perp � The values of trigonometric ratios are changed if Ø is changed. � Resolution of Vector: � The process of splitting a vector into its parts (components) is called resolution of a vector. Generally a vector is resolved into two components at right angle to each other Such components are called rectangular components. � Horizontal Component: The component which is along horizontal direction is called horizontal component. � � Vertical Component: The Component which is along vertical direction is called vertical Component

Trignometry

Trignometry � Consider a vector F, which shows the representative line AB making angle Ø with x-axis From B draw perpendicular BC on xaxis. Suppose AB and AC are represented by two Vectors. Vector BC is parallel to y-axis and y Vector AC is along x-axis. Hence we denote Vector AC by Fx and vector AB by Fy by Applying head to tail rule of vector addition, The sum of vectors Fx and Fy is equal to F. Therefore, FX and FY are rectangular components B of Vector F. � The magnitude of these components can be Fy determined by using trigonometric ratios. � Now considering right angle triangle ABC. Horizontal Component / X-Component � Vertical component / Y-Component � Cos Ø = Base/Hyp � Cos Ø = AC/BC � Cos Ø = Fx / F � Fx = FCos Ø � Sin Ø = Perp/Hyp � Sin Ø = AB / BC � Sin Ø = Fy / F � Fy = FSin Ø � � Addition of Rectangular Components of Vectors: OR � Composition of Vector: � Rectangular components of vector (components that are perpendicular to each other) can be joining together to form resultant vector or original vector. � Considering right angle triangle ABC. Where: Fx = AB = Base , Fy = BC = Perp, F = AC = Hyp � For magnitude of vector using Pythagoras theorem. � (H)2 = (B)2 + (P)2 � (AC)2 = (AB)2 + (BC)2 � AC = √(AB)2 + (BC)2 � F = √Fx 2 + Fy 2 � For direction of vector using trigonometric ratio: � Tan Ø = Perp / Base � Tan Ø = BC / AC � Tan Ø = Fy / Fx � 0 = Tan-1 (Fy / Fx)

PARALLELOGRAM LAW OF VECTOR ADDITION �Acccording to the parallelogram law of vector addition: �"If two vector quantities are represented by two adjacent sides or a parallelogram then the diagonal of parallelogram will be equal to the resultant of these two vectors. "

EXPLANATION �Consider two vectors. Let the vectors have the following orientation. According to parallelogram law:

MAGNITUDE OF RESULTANT VECTOR �Magintude or resultant vector can be determined by using either sine law or cosine law.

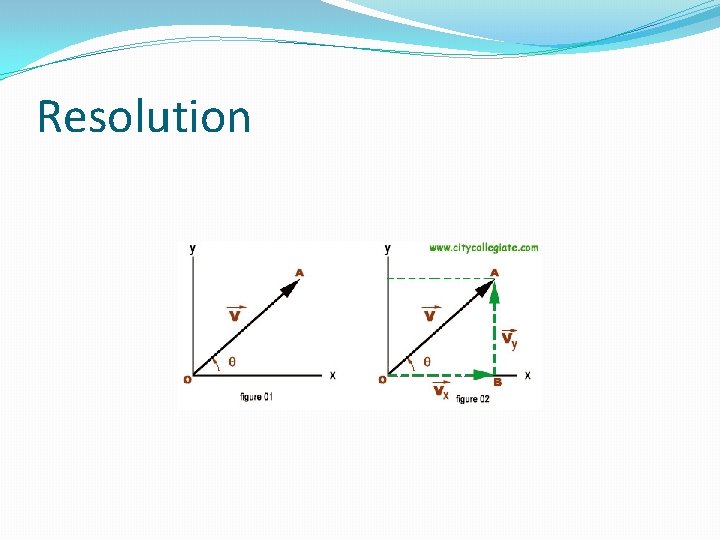
RESOLUTION OF VECTOR �DEFINITION �The process of splitting a vector into various parts or components is called "RESOLUTION OF VECTOR" �These parts of a vector may act in different directions and are called "components of vector". �We can resolve a vector into a number of components. Generally there are three components of vector viz. Component along X-axis called x-component Component along Y-axis called Y-component Component along Z-axis called Z-component �Here we will discuss only two components x-component & Y-component which are perpendicular to each other. These components are called rectangular components of vector.

METHOD OF RESOLVING A VECTOR INTO RECTANGULAR COMPONENTS �Consider a vector acting at a point making an angle q with positive X-axis. Vector is represented by a line OA. From point A draw a perpendicular AB on X-axis. Suppose OB and BA represents two vectors. Vector OA is parallel to X-axis and vector BA is parallel to Y-axis. Magnitude of these vectors are Vx and Vy respectively. By the method of head to tail we notice that the sum of these vectors is equal to vector. Thus Vx and Vy are the rectangular components of vector. Vx = Horizontal component of. Vy = Vertical component of.

Resolution

MAGNITUDE OF HORIZONTAL COMPONENT �Consider right angled triangle DOAB

MAGNITUDE OF VERTICAL COMPONENT �Consider right angled triangle DOAB

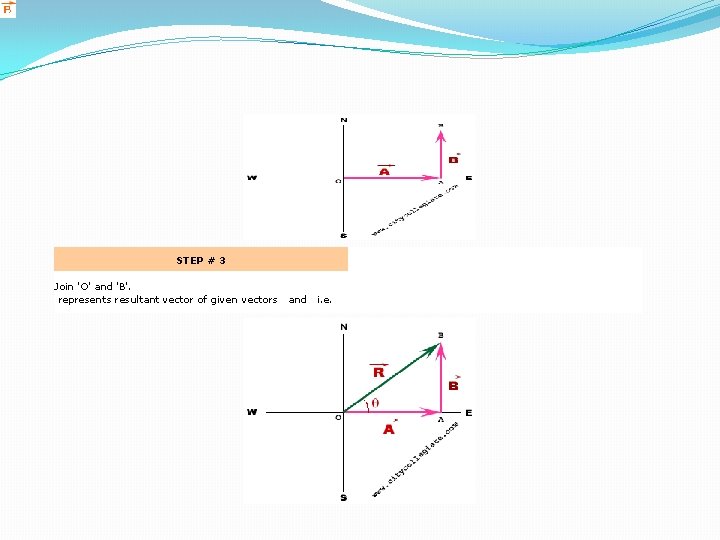
Addition of vectors by Head to Tail method (Graphical Method) �Head to Tail method or graphical method is one of the easiest method used to find the resultant vector of two of more than two vectors. �DETAILS OF METHOD. Consider two vectors and acting in the directions as shown below:

�In order to get their resultant vector by head to tail method we must follow the following steps: �STEP # 1 �Choose a suitable scale for the vectors so that they can be plotted on the paper. �STEP # 2 �Draw representative line of vector such that the tail of coincides with the head of vector.

STEP # 3 Join 'O' and 'B'. represents resultant vector of given vectors and i. e.

�STEP # 4 � �Measure the length of line segment and multiply it with the scale choosen initially to get the magnitude of resultant vector. �STEP # 5 � �The direction of the resultant vector is directed from the tail of vector to the head of vector.