CAPITAL BUDGETING TECHNIQUES n EUGENE SAULS capital budgeting

CAPITAL BUDGETING TECHNIQUES n EUGENE SAULS capital budgeting 1

Capital Budgeting Techniques n PAY-BACK n AVERAGE RATE OF RETURN n DISCOUNTED CASH FLOW capital budgeting 2

PAYBACK FORMULA PAYBACK = INVESTMENT ANNUAL CASH FLOW capital budgeting 3

PAYBACK EXAMPLE Investment = $100, 000 n Cash Flows: Year 1 $ 5, 000 Year 2 20, 000 Year 3 35, 000 Year 4 60, 000 Year 5 45, 000 n capital budgeting 4

SOLUTION TO PAYBACK n Unrecovered Investment $100, 000 95, 000 75, 000 40, 000 -20, 000 -65, 000 Investment = $100, 000 Year 1 5, 000 Year 2 20, 000 Year 3 35, 000 Year 4 60, 000 Year 5 45, 000 The payback is: 3 1/3 years capital budgeting n 5

PAYBACK EXERCISE INVESTMENT OF $250, 000 n CASH FLOWS: n YEAR 1 $-10, 000 n YEAR 2 60, 000 n YEAR 3 90, 000 n YEAR 4 120, 000 n YEAR 5 100, 000 n YEAR 6 -20, 000 n CALCULATE THE PAYBACK capital budgeting n 6

SOLUTION TO EXERCISE Unrecovered Investment n Investment = $250, 000 $ 250, 000 Year 1 -10, 000 260, 000 Year 2 60, 000 200, 000 Year 3 90, 000 110, 000 Year 4 120, 000 -10, 000 Year 5 100, 000 -110, 000 Year 6 -20, 000 - 90, 000 The payback is: 3 years and 11 months n capital budgeting 7

PAYBACK The payback method estimates the length of time it takes to recover the investment n Payback is widely used. n It is simple to understand apply HOWEVER It lacks economic substance, it disregards n The time value of money n Cash flows after the payback period capital budgeting 8

AVERAGE RATE OF RETURN FORMULA Average Positive Cash Flow R of R = Investment capital budgeting 9

RATE OF RETURN EXAMPLE Investment = $100, 000 n Cash Flows: Year 1 $ 5, 000 Year 2 20, 000 Year 3 35, 000 Year 4 60, 000 Year 5 45, 000 n capital budgeting 10

RATE OF RETURN SOLUTION Profit n 165, 000 – 100, 000 = $65, 000 n Average Profit n $65, 000 / 5 = $13, 000 per year n Average Rate of Return n 13, 000 / 100, 000 = 13% n capital budgeting 11

RATE OF RETURN EXERCISE INVESTMENT OF $250, 000 n CASH FLOWS: n YEAR 1 $ -10, 000 n YEAR 2 60, 000 n YEAR 3 90, 000 n YEAR 4 120, 000 n YEAR 5 100, 000 n YEAR 6 -20, 000 capital budgeting n CALCULATE THE RATE OF RETURN n 12

SOLUTION Profit = n 340, 000 - 250, 000 = $ 90, 000 n Average profit = n $90, 000 / 6 = $15, 000 n Rate of Return = n $15, 000 / $250, 000 = 6% n capital budgeting 13

AVERAGE RATE OF RETURN The average rate of return estimates the average rate of return over the life of the project n It is simple to apply n Considers the cash flow after payback HOWEVER Like payback, it ignores the time value of money capital budgeting 14

DISCOUNTED CASH FLOW There are two discounted cash flow techniques n Internal Rate of Return - The economic (real) rate of return on the investment n Net Present Value - The net cash value after charging a capital cost capital budgeting 15

FUTURE AMOUNT OF ONE INVEST $1, 000 IN THE BANK AT 10% n YEAR O INVESTMENT IS $1, 000 n YEAR 1 INVESTMENT IS $1, 100 n YEAR 2 INVESTMENT IS $1, 210 n YEAR 3 INVESTMENT IS $1, 331 n capital budgeting 16

FORMULA FOR THE FUTURE AMOUNT OF ONE AMOUNT = INVESTMENT ( 1 + r ) n n Where r = rate of return n n = number of years (periods) n AMOUNT is the future value n INVESTMENT is the amount put in initially, or n the PRESENT VALUE capital budgeting n 17

PRESENT VALUE FORMULA FOR SINGLE AMOUNT n Simple math on the amount formula yields n Present Value = AMOUNT / ( 1 + r ) n capital budgeting 18

APPLY FORMULA n Present value = $1, 331 / (1. 00 + 0. 10) 3 n = 1, 331 / (1. 1) 3 n = 1, 331 / 1. 331 n = $1, 000 capital budgeting 19

WHAT TO DO WHEN WE HAVE MANY CASH FLOWS? capital budgeting 20

NET PRESENT VALUE FORMULA Where: r = minimum acceptable rate of return and = cash flow in period n capital budgeting 21

DETERMINING THE INTERNAL RATE OF RETURN The Internal Rate of Return is that rate which yields a Net Present Value of zero. If cash flows are not uniform, then the solution is found by trial-and-error. capital budgeting 22

PROBLEMS WITH THE INTERNAL RATE OF RETURN There are two majors problems with the Internal Rate of Return method: n Mathematically, there can be more than one internal rate of return, one for each change in direction of cash flow and n The important thing is not the rate of return but the amount of money earned. capital budgeting 23

NPV EXAMPLE Investment = $100, 000 n Cash Flows: Year 1 $ 5, 000 Year 2 20, 000 Year 3 35, 000 Year 4 60, 000 Year 5 45, 000 n Discount Rate of 9% n capital budgeting 24

SOLUTION TO NPV EXAMPLE Cash Flows PV factor PV Investment = $-100, 000 1. 00 $ -100, 000 Year 1 5, 000. 917 4, 585 Year 2 20, 000. 842 16, 840 Year 3 35, 000. 772 27, 020 Year 4 60, 000. 708 42, 480 Year 5 45, 000. 659 29, 655 Net Present Value $ 20, 580 n capital budgeting 25
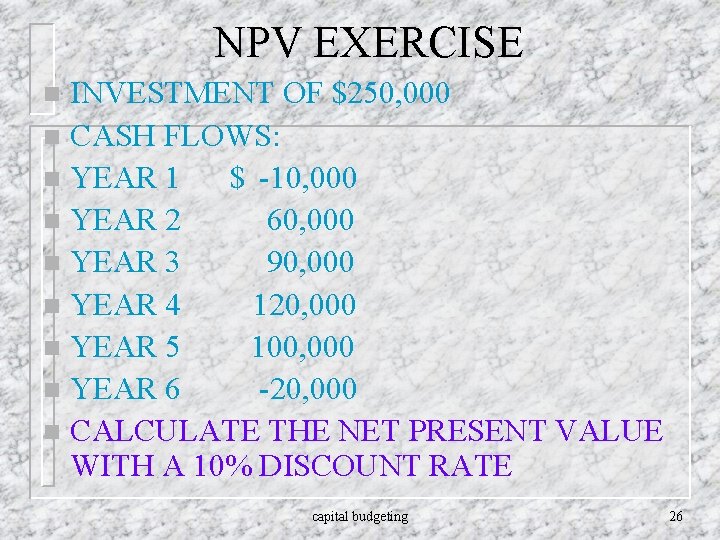
NPV EXERCISE INVESTMENT OF $250, 000 n CASH FLOWS: n YEAR 1 $ -10, 000 n YEAR 2 60, 000 n YEAR 3 90, 000 n YEAR 4 120, 000 n YEAR 5 100, 000 n YEAR 6 -20, 000 n CALCULATE THE NET PRESENT VALUE WITH A 10% DISCOUNT RATE n capital budgeting 26

SOLUTION TO NPV EXERCISE Cash Flows PV factor PV Investment $ -250, 000 1. 000 -250, 000 YEAR 1 -10, 000. 909 -9, 090 YEAR 2 60, 000. 826 49, 560 YEAR 3 90, 000. 751 67, 590 YEAR 4 120, 000. 683 81, 960 YEAR 5 100, 000. 621 62, 100 YEAR 6 -20, 000. 564 -11, 280 NET PRESENT VALUE - 9, 160 capital budgeting 27

NET PRESENT VALUE The Net Present Value method resolves all of the problems inherent in the other methods. n It considers all flows, n It considers the time value of money, n There is a unique solution, and n It solves for profit in excess of capital costs capital budgeting 28

APPLICATION OF NPV Often the NPV method is applied without regard to the relative risk of the cash flows. Only one discount rate is applied to all cash flow estimates. This approach should, inadvertently, lead to higher risk opportunities. capital budgeting 29

ADJUSTING FOR RISK There are two methods used to adjust for risk: n Adjust the cash flow or n Adjust the discount rate. The cash flow can be adjusted to the Certainty Equivalent (CE) cash flow. The Discount Rate can be adjusted directly. Conventionally, there is a direct relationship between the discount rate and risk. capital budgeting 30

Estimating the Certainty Equivalent Estimate the Cash Flow in a period: e. g. , $ 1, 000 in year 3 n Evaluate the risk of that cash flow n Estimate the amount you would be willing to receive, with certainty, instead of the $1, 000 e. g. , $ 850, 000 n Discount these CEs at the risk-free rate of return n capital budgeting 31

ADJUSTING THE DISCOUNT RATE n Estimate the cash flow in a period: e. g. , $1, 000 in year 3 n Determine the minimum rate of return that would be acceptable for the particular cash flow. capital budgeting 32
RELATIONSHIP OF RISK TO DISCOUNT RATE Discount Rate Risk capital budgeting 33
RELATIONSHIP OF DISCOUNT RATE TO NET PRESENT VALUE Discount Rate NPV capital budgeting 34

CONFLICT OF NEGATIVE CASH FLOWS n If cash flows are negative, investors should prefer lower net present values. n Lower net present values result from higher discount rates. THEREFORE capital budgeting 35

THERE SHOULD BE AN INVERSE RELATIONSHIP OF RATE OF RETURN TO RISK. THAT IS, THE GREATER THE RISK, THE LOWER THE DISCOUNT RATE. capital budgeting 36
GRAPHICALLY Discount Rate 0 RISK capital budgeting 37

capital budgeting 38

PROPOSED SOLUTION n Group cash flows according to the activities that drive the cash flows. n If the net cash flow is positive, discount in the conventional method, i. e. , the greater the risk, the greater the discount rate. n If the net cash flow is negative, adjust the discount rate inversely to risk. capital budgeting 39

WHAT METHODS ARE GENERALLY USED? n Studies indicate that the payback method is widely used, probably the most used. n Net present value, without adjusting for risk, is the second most common method. n Many companies use a combination of these two methods. However, I suspect that the MOST commonly used method is: capital budgeting 40

I WANT IT capital budgeting 41
- Slides: 41