1 CapitalBudgeting Techniques Chapter 9 Capital Budgeting Concepts

1 Capital-Budgeting Techniques Chapter 9

Capital Budgeting Concepts v Capital Budgeting involves evaluation of (and decision about) projects. Which projects should be accepted? Here, our goal is to accept a project which maximizes the shareholder wealth. Benefits are worth more than the cost. v The Capital Budgeting is based on forecasting. v Estimate future expected cash flows. v Evaluate project based on the evaluation method. v Classification of Projects v. Mutually Exclusive - accept ONE project only v. Independent - accept ALL profitable projects. 2

Capital Budgeting Concepts Cash Flows v Initial Cash Outlay - amount of capital spent to get project going. 3

Capital Budgeting Concepts 4 Cash Flows v Initial Cash Outlay - amount of capital spent to get project going. v If spend $10 million to build new plant then the Initial Outlay (IO) = $10 million CF 0 = Cash Flow time 0 = -10 million

Capital Budgeting Concepts 5 Cash Flows v Initial Cash Outlay - amount of capital spent to get project going. v If spend $10 million to build new plant then the Initial Outlay (IO) = $10 million CF 0 = Cash Flow time 0 = -10 million v. Annual Cash Inflows--after-tax CF v. Cash inflows from the project CFn = Sales - Costs We will determine these in Chapter 10

Capital Budgeting Methods 6 Payback Period v Number of years needed to recover your initial outlay.

Capital Budgeting Methods 7 Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 P R O J E C T A B (10, 000. ) 3, 500 500 4, 600 10, 000

8 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 (10, 000) 1 3, 500 P R O J E C T A B (10, 000. ) 3, 500 2 3, 500 500 4, 600 10, 000 3 3, 500 4 3, 500

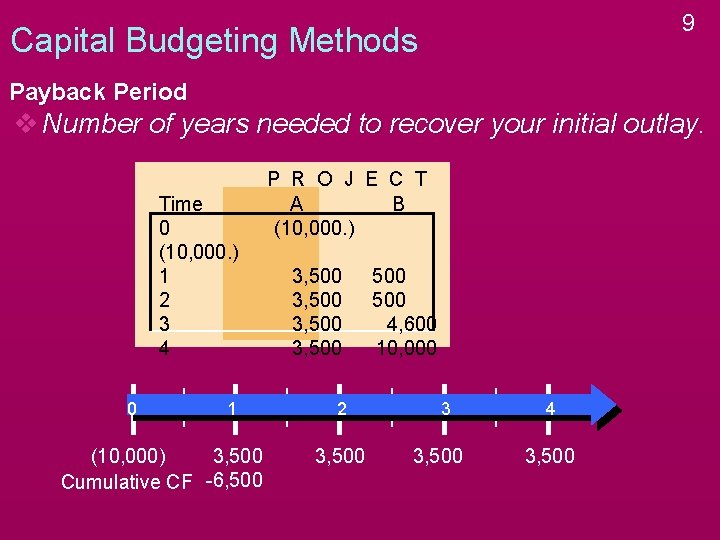
9 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 1 (10, 000) 3, 500 Cumulative CF -6, 500 P R O J E C T A B (10, 000. ) 3, 500 2 3, 500 500 4, 600 10, 000 3 3, 500 4 3, 500

10 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 1 (10, 000) 3, 500 Cumulative CF -6, 500 P R O J E C T A B (10, 000. ) 3, 500 2 3, 500 -3, 000 500 4, 600 10, 000 3 3, 500 4 3, 500

11 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 1 (10, 000) 3, 500 Cumulative CF -6, 500 P R O J E C T A B (10, 000. ) 3, 500 2 3, 500 -3, 000 500 4, 600 10, 000 3 3, 500 +500 4 3, 500

12 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 1 (10, 000) 3, 500 Cumulative CF -6, 500 P R O J E C T A B (10, 000. ) 3, 500 2 3, 500 -3, 000 500 4, 600 10, 000 3 3, 500 +500 4 3, 500 Payback 2. 86 years

Capital Budgeting Methods 13 Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 P R O J E C T A B (10, 000. ) 3, 500 500 4, 600 10, 000

14 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 (10, 000) P R O J E C T A B (10, 000. ) 3, 500 1 2 500 500 4, 600 10, 000 3 4, 600 4 10, 000

15 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 1 (10, 000) 500 Cumulative CF -9, 500 P R O J E C T A B (10, 000. ) 3, 500 2 500 500 4, 600 10, 000 3 4, 600 4 10, 000

16 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 1 (10, 000) 500 Cumulative CF -9, 500 P R O J E C T A B (10, 000. ) 3, 500 2 500 -9, 000 500 4, 600 10, 000 3 4, 600 4 10, 000

17 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 1 (10, 000) 500 Cumulative CF -9, 500 P R O J E C T A B (10, 000. ) 3, 500 2 500 -9, 000 500 4, 600 10, 000 3 4, 600 -4, 400 4 10, 000

18 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 1 (10, 000) 500 Cumulative CF -9, 500 P R O J E C T A B (10, 000. ) 3, 500 2 500 -9, 000 500 4, 600 10, 000 3 4, 600 -4, 400 4 10, 000 +5, 600

19 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 1 (10, 000) 500 Cumulative CF -9, 500 P R O J E C T A B (10, 000. ) 3, 500 2 500 -9, 000 500 4, 600 10, 000 3 4, 600 -4, 400 4 10, 000 +5, 600 Payback = 3. 44 years

20 Capital Budgeting Methods Payback Period v Number of years needed to recover your initial outlay. Time 0 (10, 000. ) 1 2 3 4 0 1 (10, 000) 500 Cumulative CF -9, 500 Evaluation: Company sets maximum acceptable payback. If Max PB = 3 years, accept 500 project A and reject 500 project C 4, 600 P R O J E C T A B (10, 000. ) 3, 500 2 500 -9, 000 10, 000 3 4, 600 -4, 400 4 10, 000 +5, 600 Payback 3. 44 years

21 • Payback Method The payback method is not a good method as it does not consider the time value of money. Which project should you choose? CF 0 A -100, 000 B -100, 000 CF 1 90, 000 1, 000 CF 2 9, 000 CF 3 1, 000 90, 000

• Payback Method 22 The Discounted payback method can correct this shortcoming of the payback method. To find the discounted pay back (1) Find the PV of each cash flow on the time line. (2) Find the payback using the discounted CF and NOT the CF. Example In Table 9 -2

• Payback Method 23 Also, the payback method is not a good method as it does not consider the cash flows beyond the payback period.

Payback Method 24 Also, the payback method is not a good method as it does not consider the cash flows beyond the payback period. Which project should you choose? CF 0 CF 1 CF 2 Cf 3 CF 4 A -100000 90000 10000 0 0 B -100000 9000 80000 1000000

25 Payback Method Also, the payback method is not a good method as it does not consider the cash flows beyond the payback period. Which project should you choose? CF 0 CF 1 CF 2 Cf 3 A -100, 000 90, 000 10, 000 0 B -100, 000 9, 000 80, 000 CF 4 0 100, 0000 These two shortcomings often result in an incorrect decisions.

Capital Budgeting Methods that consider time value of money and all cash flows Net Present Value: Present Value of all costs and benefits of a project. 26

Capital Budgeting Methods Net Present Value of all costs and benefits of a project. Concept is similar to Intrinsic Value of a security but subtracts cost of the project. NPV = PV of Inflows - Initial Outlay 27

Capital Budgeting Methods 28 Net Present Value v Present Value of all costs and benefits of a project. v Concept is similar to Intrinsic Value of a security but subtracts of cost of project. NPV = PV of Inflows - Initial Outlay NPV = CF 1 (1+ k ) + CF 2 (1+ k )2 CF 3 CFn + (1+ +···+ – IO 3 n k) (1+ k )

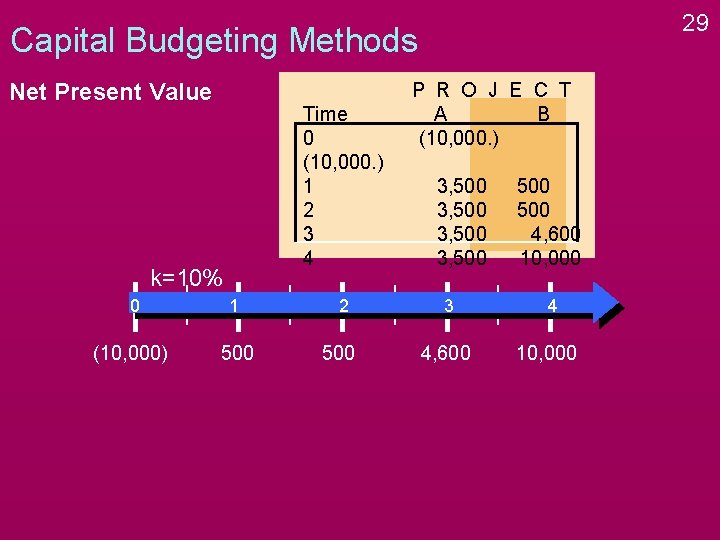
29 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 (10, 000) 500 2 500 P R O J E C T A B (10, 000. ) 3, 500 3 4, 600 500 4, 600 10, 000 4 10, 000

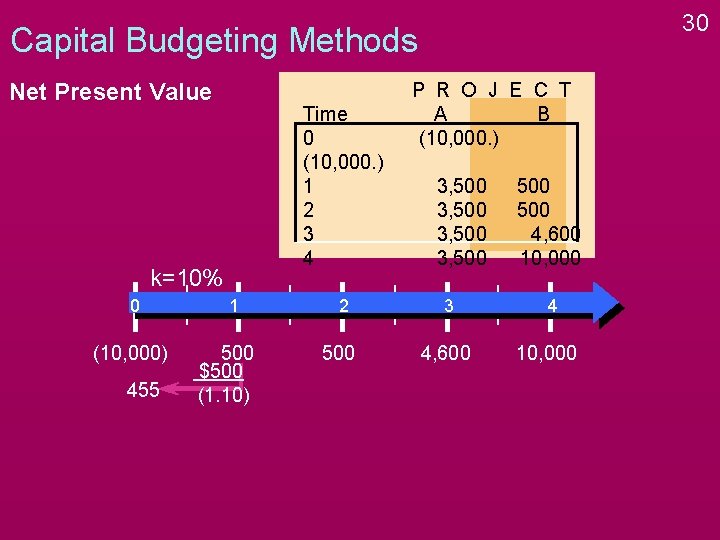
30 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 (10, 000) 455 1 500 $500 (1. 10) 2 500 P R O J E C T A B (10, 000. ) 3, 500 3 4, 600 500 4, 600 10, 000 4 10, 000

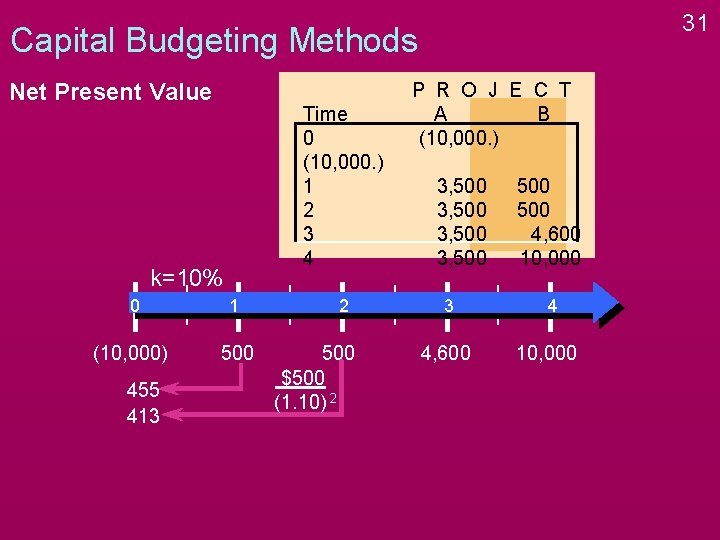
31 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 (10, 000) 500 455 413 2 500 $500 (1. 10) 2 P R O J E C T A B (10, 000. ) 3, 500 3 4, 600 500 4, 600 10, 000 4 10, 000

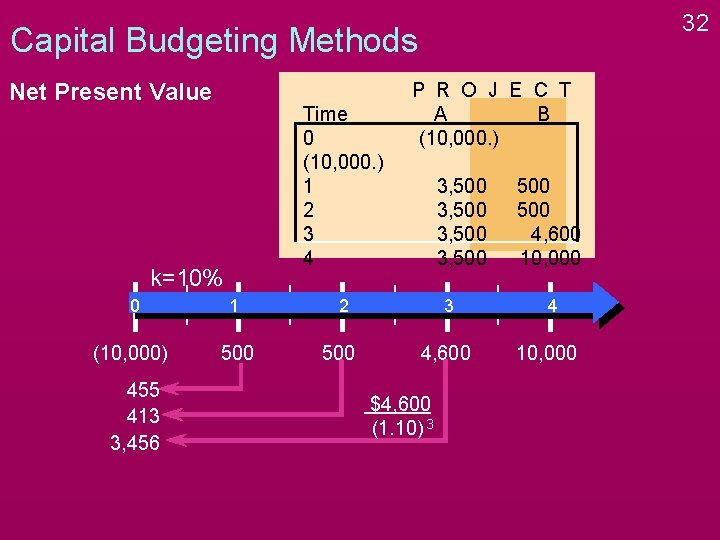
32 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 (10, 000) 500 455 413 3, 456 P R O J E C T A B (10, 000. ) 3, 500 2 500 3 4, 600 $4, 600 (1. 10) 3 500 4, 600 10, 000 4 10, 000

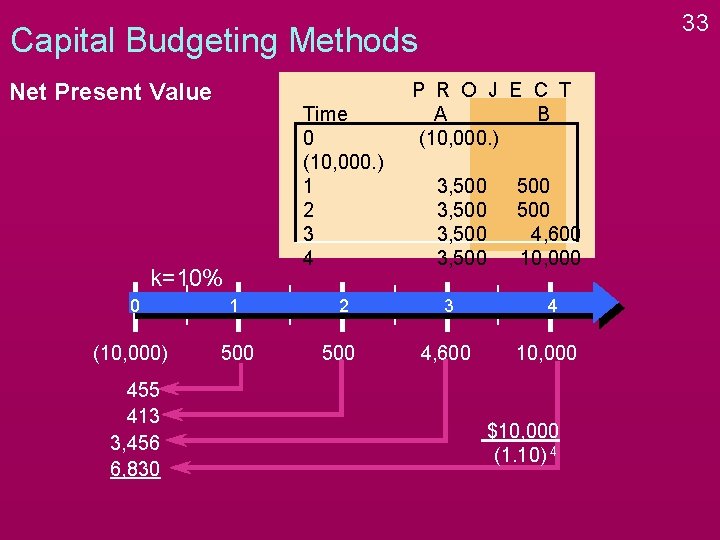
33 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 (10, 000) 500 455 413 3, 456 6, 830 2 500 P R O J E C T A B (10, 000. ) 3, 500 3 4, 600 500 4, 600 10, 000 4 10, 000 $10, 000 (1. 10) 4

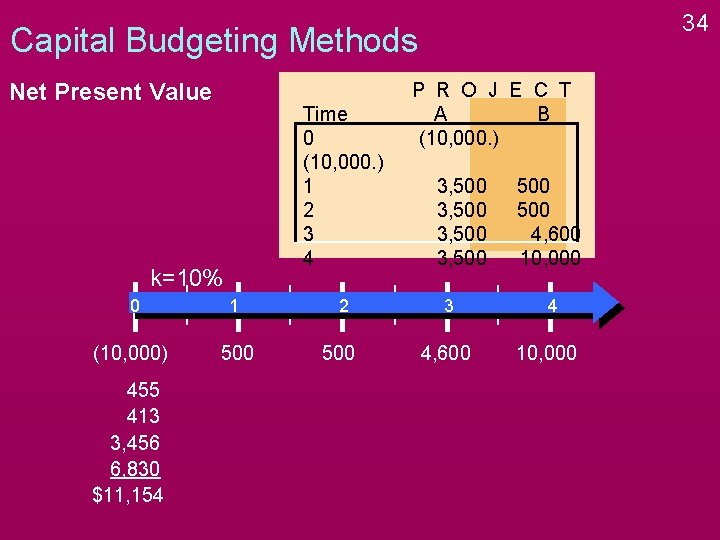
34 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 (10, 000) 500 455 413 3, 456 6, 830 $11, 154 2 500 P R O J E C T A B (10, 000. ) 3, 500 3 4, 600 500 4, 600 10, 000 4 10, 000

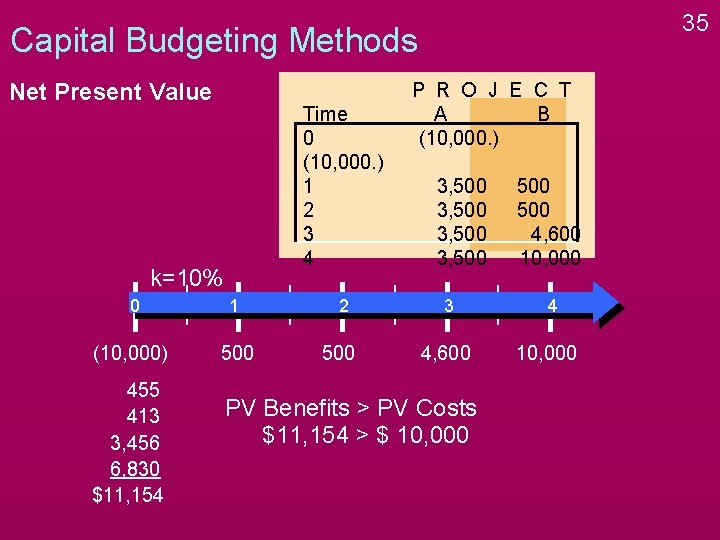
35 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 (10, 000) 500 455 413 3, 456 6, 830 $11, 154 2 500 P R O J E C T A B (10, 000. ) 3, 500 3 4, 600 PV Benefits > PV Costs $11, 154 > $ 10, 000 500 4, 600 10, 000 4 10, 000

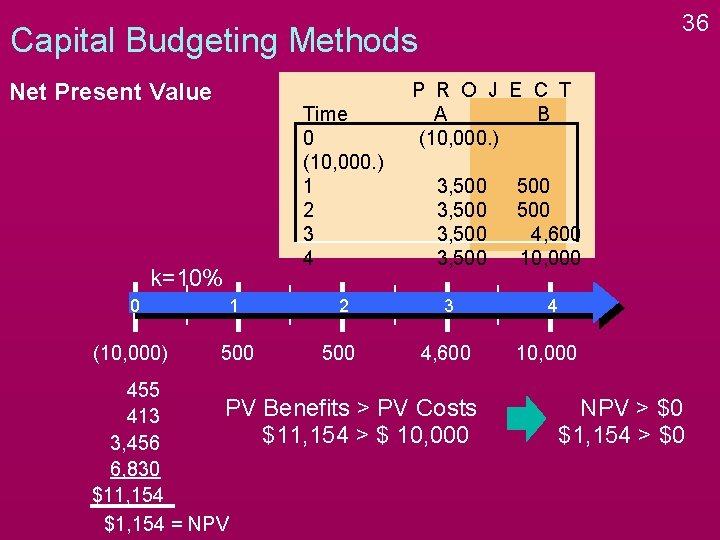
36 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 (10, 000) 500 2 500 P R O J E C T A B (10, 000. ) 3, 500 3 4, 600 455 PV Benefits > PV Costs 413 $11, 154 > $ 10, 000 3, 456 6, 830 $11, 154 $1, 154 = NPV 500 4, 600 10, 000 4 10, 000 NPV > $0 $1, 154 > $0

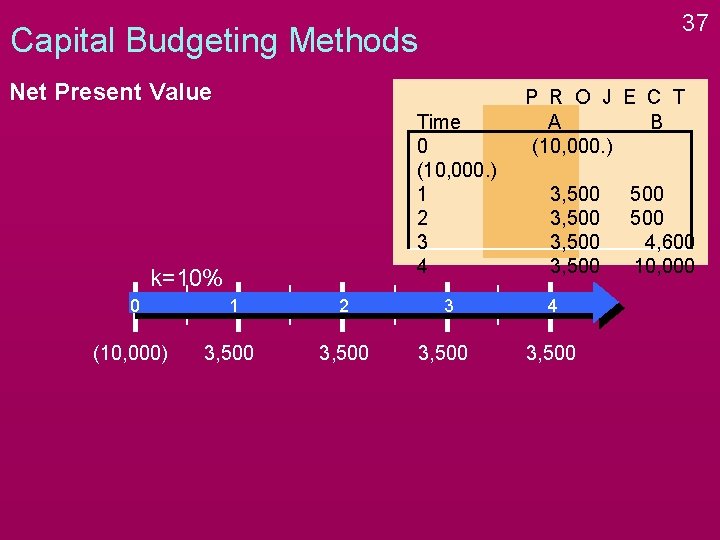
37 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 2 (10, 000) 3, 500 3 3, 500 P R O J E C T A B (10, 000. ) 3, 500 4 3, 500 500 4, 600 10, 000

38 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 2 (10, 000) 3, 500 NPV = 3, 500 (1+. 1 ) + 3 3, 500 P R O J E C T A B (10, 000. ) 3, 500 500 4, 600 10, 000 4 3, 500 (1+. 1)2 + (1+. 1 )3+ (1+. 1 )4 – 10, 000

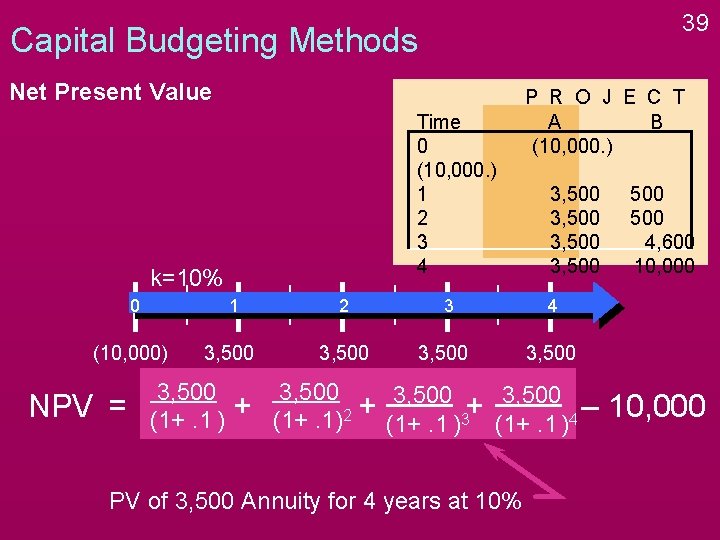
39 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 2 (10, 000) 3, 500 NPV = 3, 500 (1+. 1 ) + 3 3, 500 P R O J E C T A B (10, 000. ) 3, 500 4 3, 500 (1+. 1)2 + (1+. 1 )3+ (1+. 1 )4 – PV of 3, 500 Annuity for 4 years at 10% 500 4, 600 10, 000

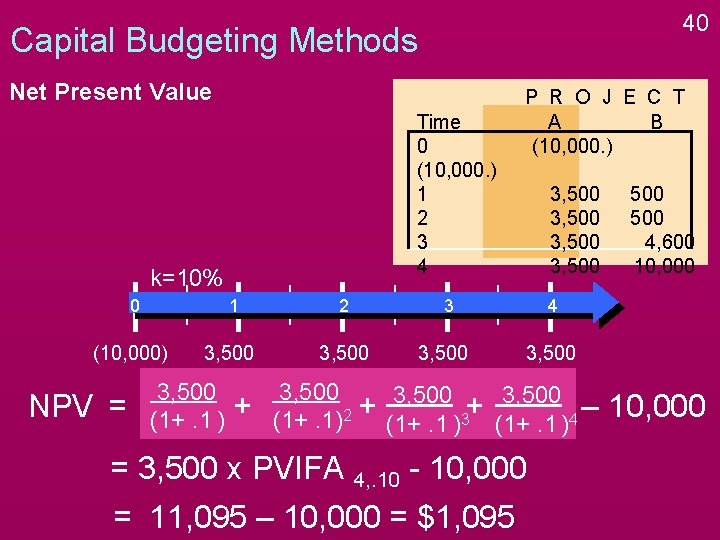
40 Capital Budgeting Methods Net Present Value Time 0 (10, 000. ) 1 2 3 4 k=10% 0 1 2 (10, 000) 3, 500 NPV = 3, 500 (1+. 1 ) + P R O J E C T A B (10, 000. ) 3, 500 3 3, 500 4 3, 500 (1+. 1)2 + (1+. 1 )3+ (1+. 1 )4 – = 3, 500 x PVIFA 4, . 10 - 10, 000 = 11, 095 – 10, 000 = $1, 095 500 4, 600 10, 000

41 Capital Budgeting Methods NPV Decision Rules v If projects are independent then accept all projects with NPV ³ 0. ACCEPT A & B

42 Capital Budgeting Methods NPV Decision Rules v If projects are independent then accept all projects with NPV ³ 0. v If projects are mutually exclusive, accept projects with higher NPV. ACCEPT A & B ACCEPT B only

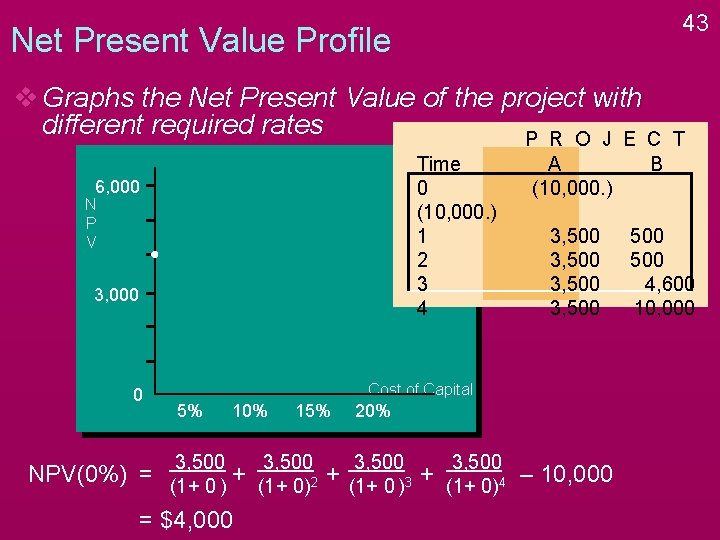
43 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V 3, 000 0 A (10, 000. ) B 3, 500 500 4, 600 10, 000 Cost of Capital 5% 3, 500 10% 15% 3, 500 20% 3, 500 T NPV(0%) = (1+ 0 ) + (1+ 0)2 + (1+ 0 )3 + (1+ 0)4 – 10, 000 = $4, 000

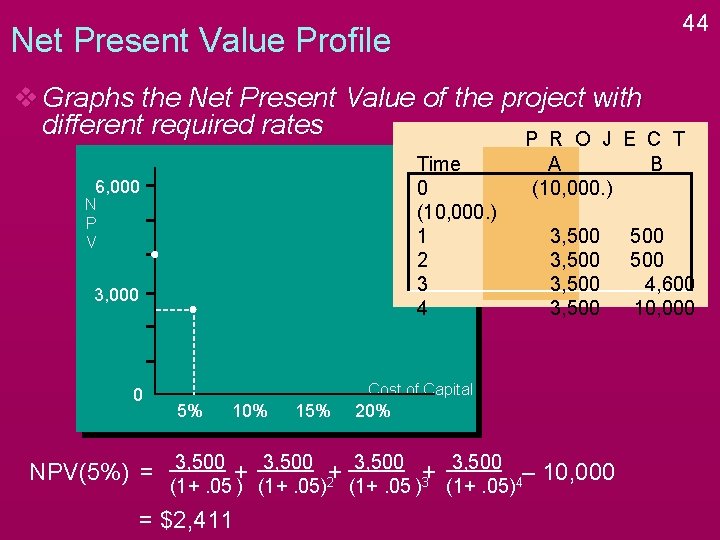
44 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V 3, 000 0 A (10, 000. ) B 3, 500 500 4, 600 10, 000 Cost of Capital 5% 10% 15% 20% NPV(5%) = 3, 500 + 3, 500 2+ 3, 500 3+ 3, 500 4– 10, 000 (1+. 05 ) (1+. 05) = $2, 411 (1+. 05 ) (1+. 05) T

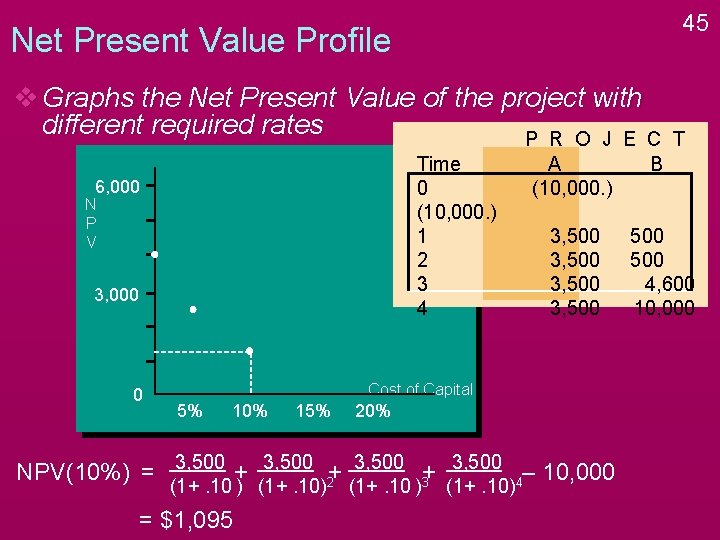
45 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V 3, 000 0 A (10, 000. ) B 3, 500 500 4, 600 10, 000 Cost of Capital 5% 10% 15% 20% NPV(10%) = 3, 500 + 3, 500 2+ 3, 500 3+ 3, 500 4– 10, 000 (1+. 10 ) (1+. 10) = $1, 095 (1+. 10 ) (1+. 10) T

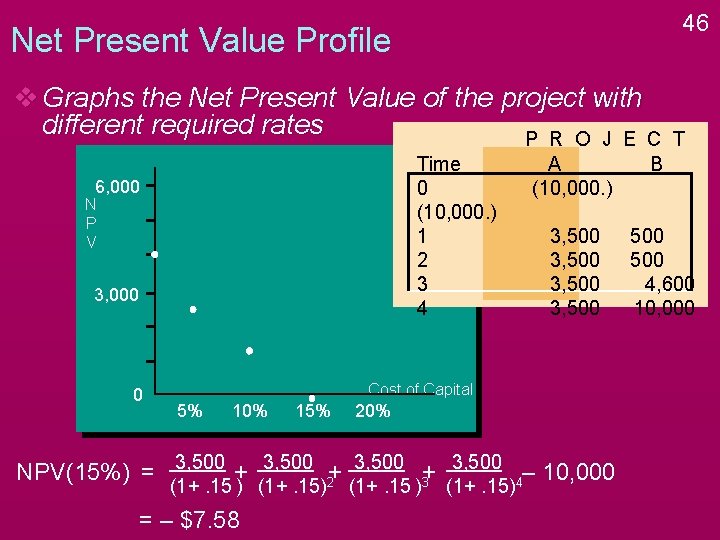
46 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V 3, 000 0 A (10, 000. ) B 3, 500 500 4, 600 10, 000 Cost of Capital 5% 10% 15% 20% NPV(15%) = 3, 500 + 3, 500 2+ 3, 500 3+ 3, 500 4– 10, 000 (1+. 15 ) (1+. 15) = – $7. 58 (1+. 15 ) (1+. 15) T

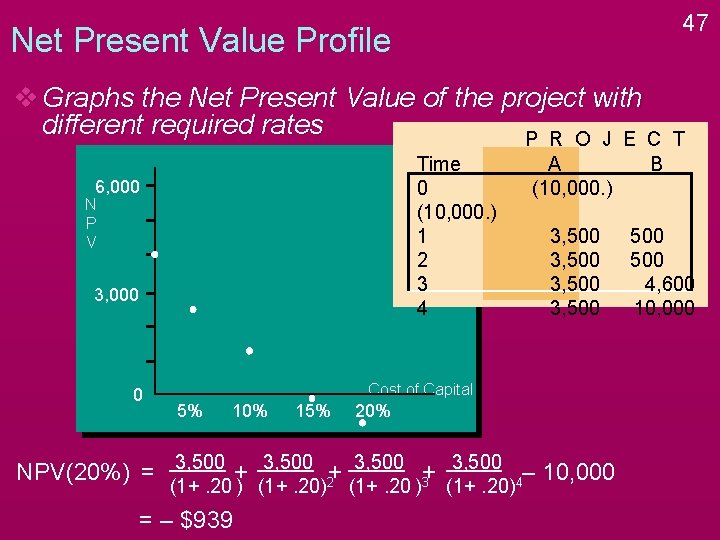
47 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V 3, 000 0 A (10, 000. ) B 3, 500 500 4, 600 10, 000 Cost of Capital 5% 10% 15% 20% NPV(20%) = 3, 500 + 3, 500 2+ 3, 500 3+ 3, 500 4– 10, 000 (1+. 20 ) (1+. 20) = – $939 (1+. 20 ) (1+. 20) T

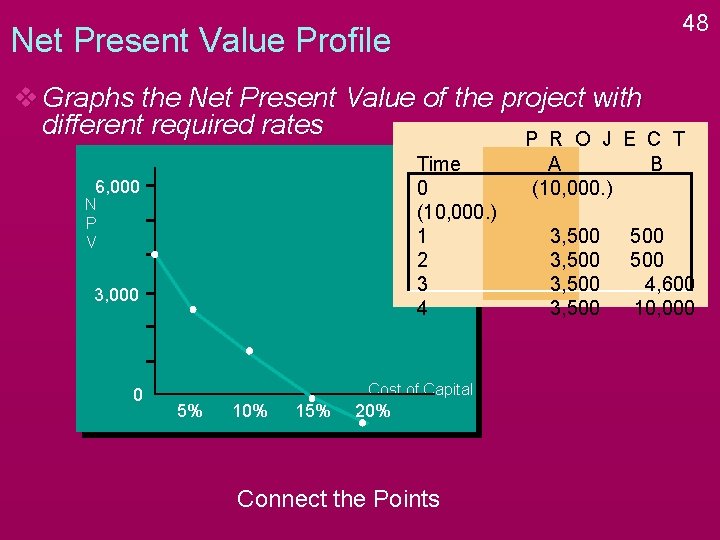
48 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V 3, 000 0 Cost of Capital 5% 10% 15% 20% Connect the Points T A (10, 000. ) B 3, 500 500 4, 600 10, 000

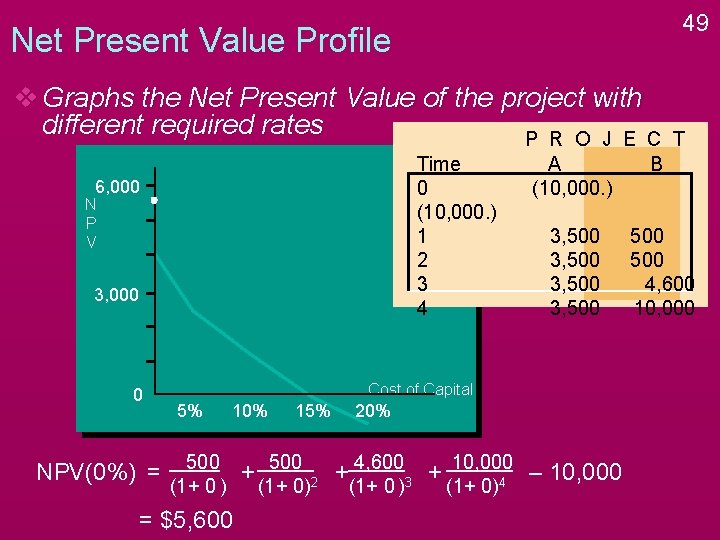
49 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V 3, 000 0 NPV(0%) = A (10, 000. ) B 3, 500 500 4, 600 10, 000 Cost of Capital 5% 10% 500 (1+ 0 ) = $5, 600 15% + 500 (1+ 0)2 20% + 4, 600 3 + 10, 000 – 10, 000 4 (1+ 0 ) (1+ 0) T

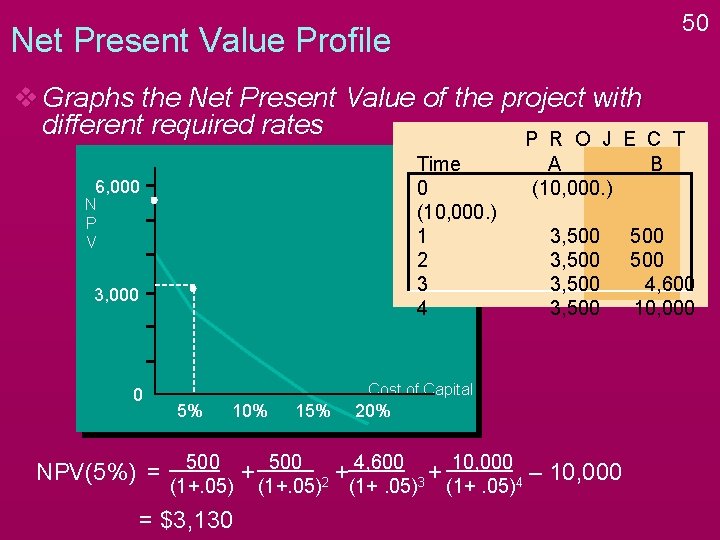
50 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V 3, 000 0 NPV(5%) = A (10, 000. ) B 3, 500 500 4, 600 10, 000 Cost of Capital 5% 10% 500 (1+. 05) = $3, 130 15% + 500 (1+. 05) 20% 4, 600 + 2 (1+. 05) 10, 000 + – 10, 000 3 4 (1+. 05) T

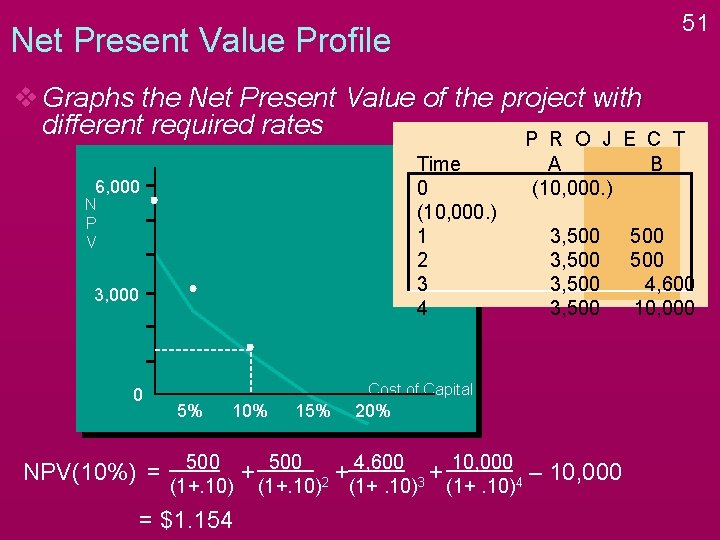
51 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V 3, 000 0 NPV(10%) = A (10, 000. ) B 3, 500 500 4, 600 10, 000 Cost of Capital 5% 10% 500 (1+. 10) = $1. 154 15% + 500 (1+. 10) 20% 4, 600 + 2 (1+. 10) 10, 000 + – 10, 000 3 4 (1+. 10) T

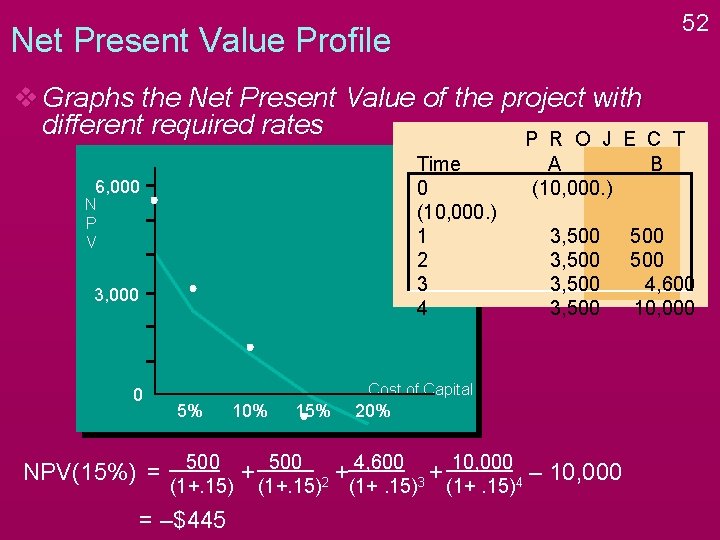
52 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V 3, 000 0 NPV(15%) = A (10, 000. ) B 3, 500 500 4, 600 10, 000 Cost of Capital 5% 10% 500 (1+. 15) = –$445 15% + 500 (1+. 15) 20% 4, 600 + 2 (1+. 15) 10, 000 + – 10, 000 3 4 (1+. 15) T

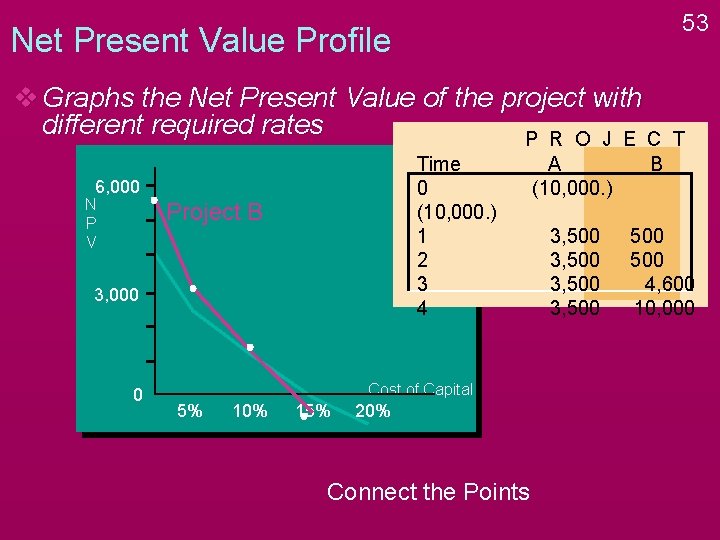
53 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V Project B 3, 000 0 Cost of Capital 5% 10% 15% 20% Connect the Points T A (10, 000. ) B 3, 500 500 4, 600 10, 000

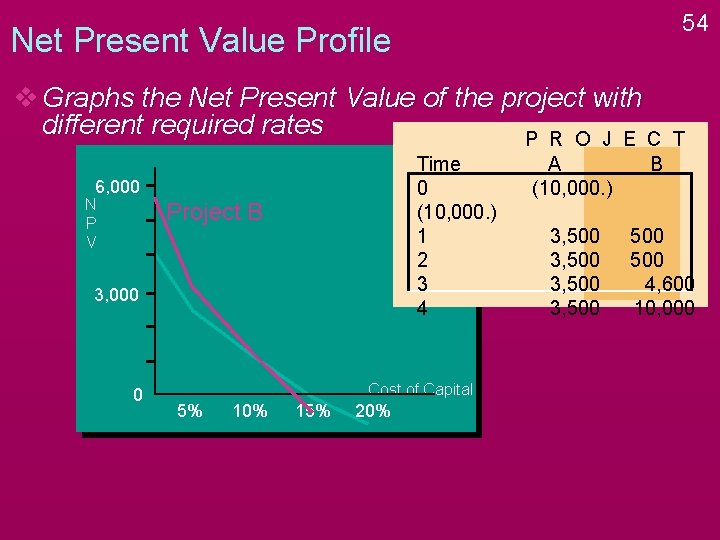
54 Net Present Value Profile v Graphs the Net Present Value of the project with different required rates P R O J E C Time 0 (10, 000. ) 1 2 3 4 6, 000 N P V Project B 3, 000 0 Cost of Capital 5% 10% 15% 20% T A (10, 000. ) B 3, 500 500 4, 600 10, 000

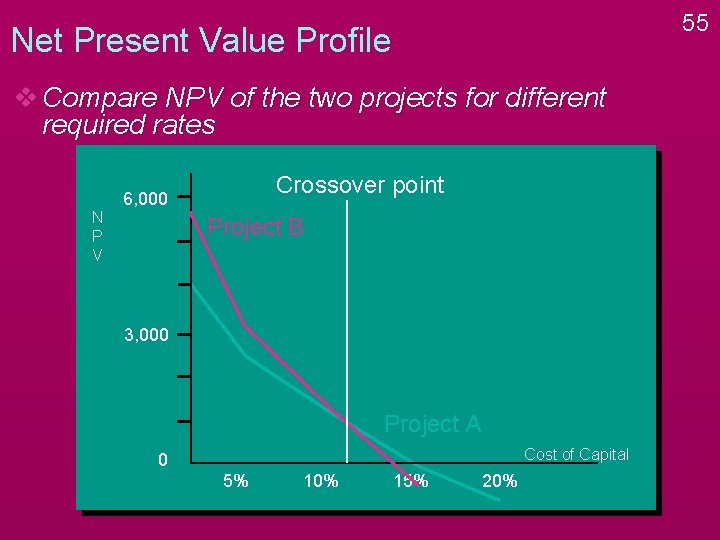
55 Net Present Value Profile v Compare NPV of the two projects for different required rates Crossover point 6, 000 N P V Project B 3, 000 Project A Cost of Capital 0 5% 10% 15% 20%

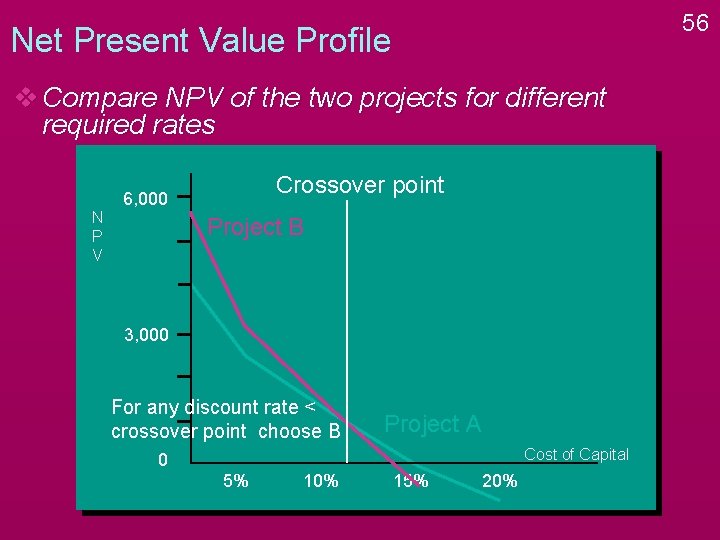
56 Net Present Value Profile v Compare NPV of the two projects for different required rates Crossover point 6, 000 N P V Project B 3, 000 For any discount rate < crossover point choose B Project A Cost of Capital 0 5% 10% 15% 20%

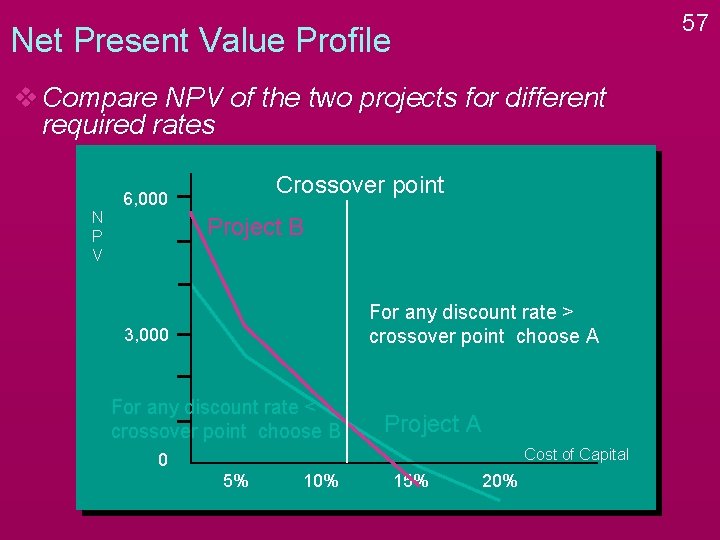
57 Net Present Value Profile v Compare NPV of the two projects for different required rates Crossover point 6, 000 N P V Project B For any discount rate > crossover point choose A 3, 000 For any discount rate < crossover point choose B Project A Cost of Capital 0 5% 10% 15% 20%

Capital Budgeting Methods Internal Rate of Return v. Measures the rate of return that will make the PV of future CF equal to the initial outlay. Definition: The IRR is that discount rate at which NPV = 0 IRR is like the YTM. It is the same cocept but the term YTM is used only for bonds. 58

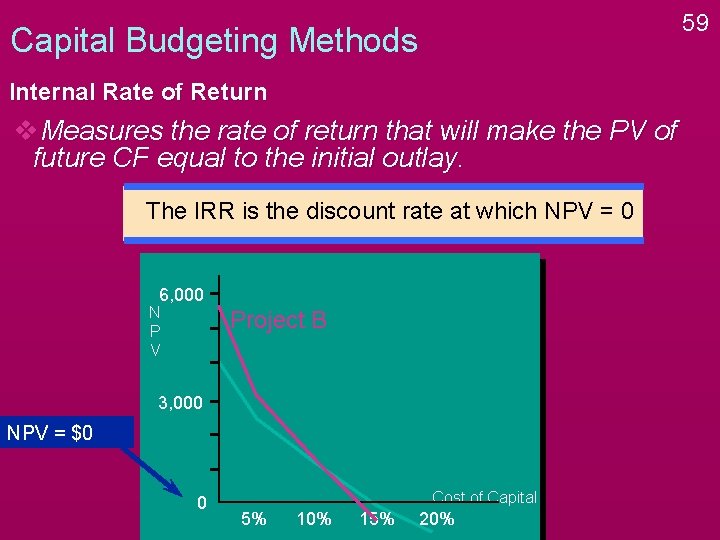
59 Capital Budgeting Methods Internal Rate of Return v. Measures the rate of return that will make the PV of future CF equal to the initial outlay. The IRR is the discount rate at which NPV = 0 6, 000 N P V Project B 3, 000 NPV = $0 0 Cost of Capital 5% 10% 15% 20%

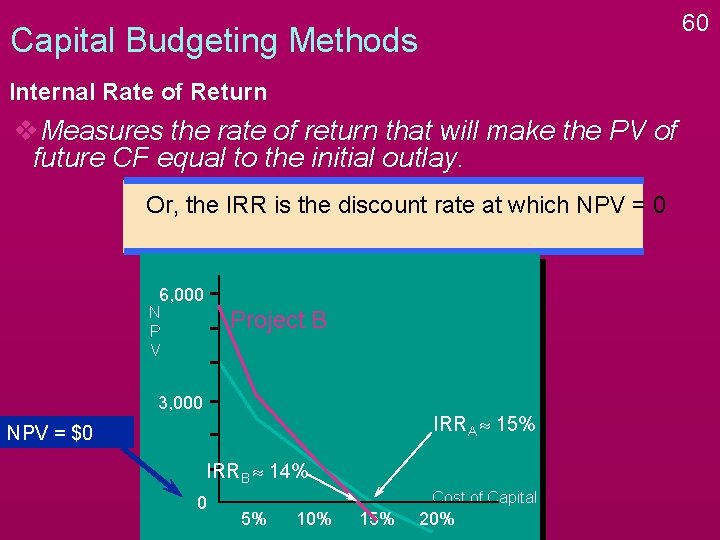
60 Capital Budgeting Methods Internal Rate of Return v. Measures the rate of return that will make the PV of future CF equal to the initial outlay. Or, the IRR is the discount rate at which NPV = 0 6, 000 N P V Project B 3, 000 IRRA » 15% NPV = $0 IRRB » 14% 0 Cost of Capital 5% 10% 15% 20%

Capital Budgeting Methods Internal Rate of Return v. Determine the mathematical solution for IRR 61

62 Capital Budgeting Methods Internal Rate of Return v. Determine the mathematical solution for IRR 0 = NPV = CF 1 CF 2 CFn + +···+ – 2 n (1+ IRR ) IO

63 Capital Budgeting Methods Internal Rate of Return v. Determine the mathematical solution for IRR 0 = NPV = IO = CF 1 CF 2 CFn + +···+ – 2 n (1+ IRR ) CF 1 CF 2 CFn + +···+ 2 (1+ IRR )n Outflow = PV of Inflows IO

64 Capital Budgeting Methods Internal Rate of Return v. Determine the mathematical solution for IRR 0 = NPV = IO = CF 1 CF 2 CFn + +···+ – 2 n (1+ IRR ) CF 1 CF 2 CFn + +···+ 2 (1+ IRR )n Outflow = PV of Inflows Solve for Discount Rates IO

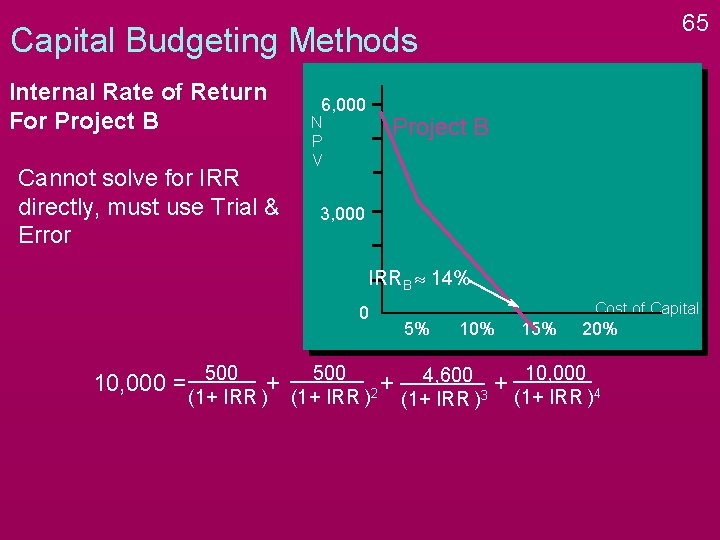
65 Capital Budgeting Methods Internal Rate of Return For Project B Cannot solve for IRR directly, must use Trial & Error 6, 000 Project B N P V 3, 000 IRRB » 14% 0 10, 000 = 500 + (1+ IRR ) Cost of Capital 5% 10% 15% 20% 500 4, 600 + 10, 000 + (1+ IRR )2 (1+ IRR )3 (1+ IRR )4

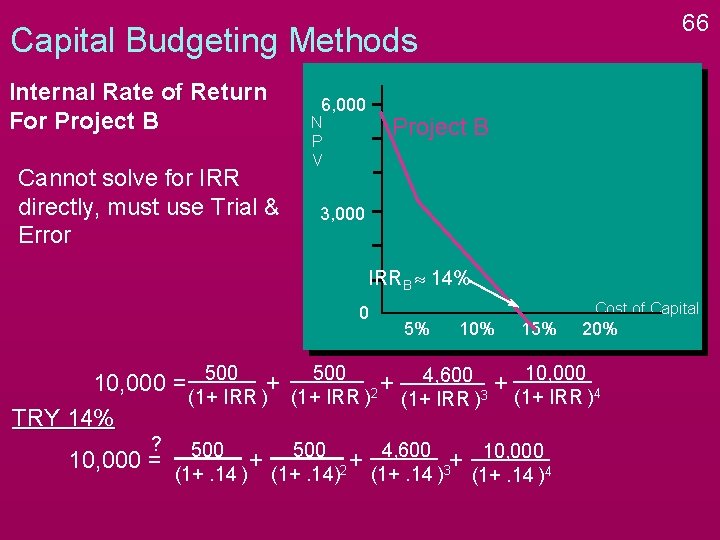
66 Capital Budgeting Methods Internal Rate of Return For Project B Cannot solve for IRR directly, must use Trial & Error 6, 000 Project B N P V 3, 000 IRRB » 14% 0 Cost of Capital 5% 10% 15% 20% 10, 000 = 500 + 500 2 + 4, 600 3 + 10, 000 4 (1+ IRR ) TRY 14% ? 10, 000 = 500 + 500 2 + 4, 600 3+ 10, 000 4 (1+. 14 )

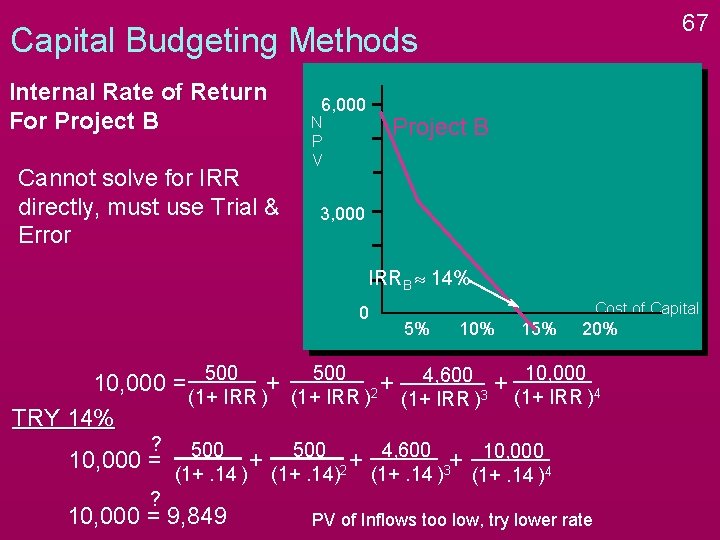
67 Capital Budgeting Methods Internal Rate of Return For Project B Cannot solve for IRR directly, must use Trial & Error 6, 000 Project B N P V 3, 000 IRRB » 14% 0 Cost of Capital 5% 10% 15% 20% 10, 000 = 500 + 500 2 + 4, 600 3 + 10, 000 4 (1+ IRR ) TRY 14% ? 10, 000 = ? 500 + 500 2 + 4, 600 3+ 10, 000 4 (1+. 14 ) 10, 000 = 9, 849 PV of Inflows too low, try lower rate

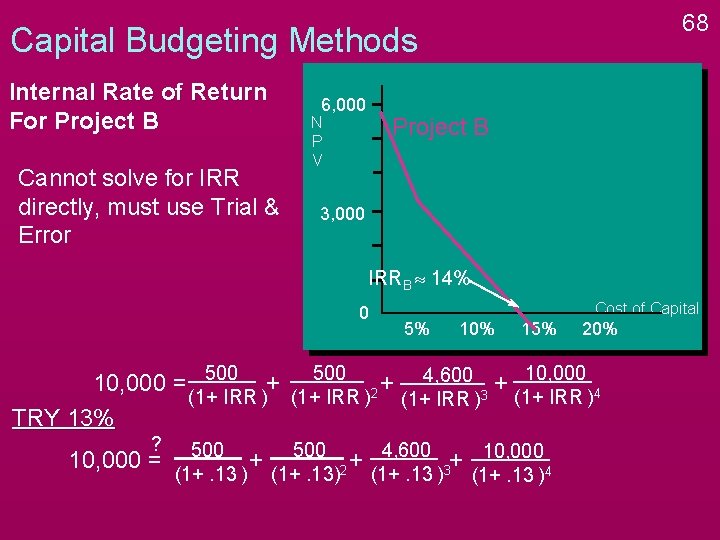
68 Capital Budgeting Methods Internal Rate of Return For Project B Cannot solve for IRR directly, must use Trial & Error 6, 000 Project B N P V 3, 000 IRRB » 14% 0 Cost of Capital 5% 10% 15% 20% 10, 000 = 500 + 500 2 + 4, 600 3 + 10, 000 4 (1+ IRR ) TRY 13% ? 10, 000 = 500 + 500 2 + 4, 600 3+ 10, 000 4 (1+. 13 )

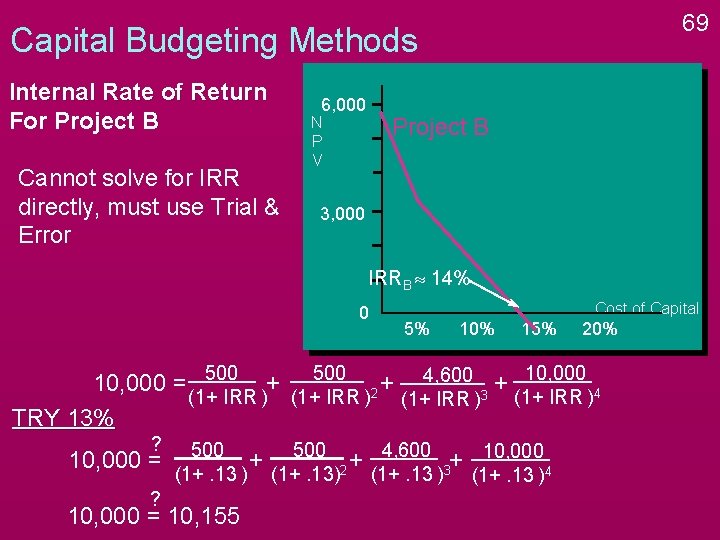
69 Capital Budgeting Methods Internal Rate of Return For Project B Cannot solve for IRR directly, must use Trial & Error 6, 000 Project B N P V 3, 000 IRRB » 14% 0 Cost of Capital 5% 10% 15% 20% 10, 000 = 500 + 500 2 + 4, 600 3 + 10, 000 4 (1+ IRR ) TRY 13% ? 10, 000 = ? 500 + 500 2 + 4, 600 3+ 10, 000 4 (1+. 13 ) 10, 000 = 10, 155

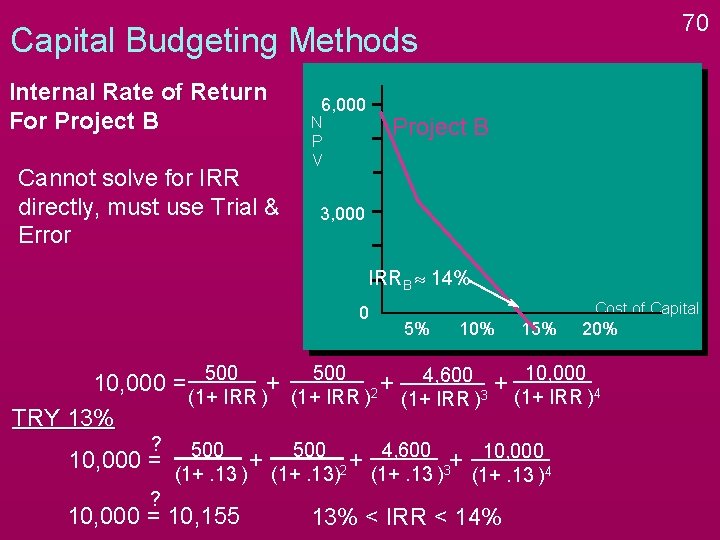
70 Capital Budgeting Methods Internal Rate of Return For Project B Cannot solve for IRR directly, must use Trial & Error 6, 000 Project B N P V 3, 000 IRRB » 14% 0 Cost of Capital 5% 10% 15% 20% 10, 000 = 500 + 500 2 + 4, 600 3 + 10, 000 4 (1+ IRR ) TRY 13% ? 10, 000 = ? 500 + 500 2 + 4, 600 3+ 10, 000 4 (1+. 13 ) 10, 000 = 10, 155 13% < IRR < 14%

Capital Budgeting Methods Decision Rule for Internal Rate of Return Independent Projects Accept Projects with IRR ³ required rate Mutually Exclusive Projects Accept project with highest IRR ³ required rate 71

Capital Budgeting Methods Profitability Index Very Similar to Net Present Value PI = PV of Inflows Initial Outlay 72

Capital Budgeting Methods Profitability Index Very Similar to Net Present Value PI = PV of Inflows Initial Outlay Instead of Subtracting the Initial Outlay from the PV of Inflows, the Profitability Index is the ratio of Initial Outlay to the PV of Inflows. 73

Capital Budgeting Methods Profitability Index Very Similar to Net Present Value PI = PV of Inflows Initial Outlay Instead of Subtracting the Initial Outlay from the PV of Inflows, the Profitability Index is the ratio of Initial Outlay to the PV of Inflows. PI = CF 1 (1+ k ) + CF 2 CF 3 CFn (1+ k )2 + (1+ k )3+···+(1+ k )n IO 74

75 Capital Budgeting Methods Profitability Index for Project B PI = 500 4, 600 10, 000 500 + + + (1+. 1 ) (1+. 1)2 (1+. 1 )3 (1+. 1 )4 10, 000 Time 0 (10, 000. ) 1 2 3 4 P R O J E C T A B (10, 000. ) 3, 500 500 4, 600 10, 000

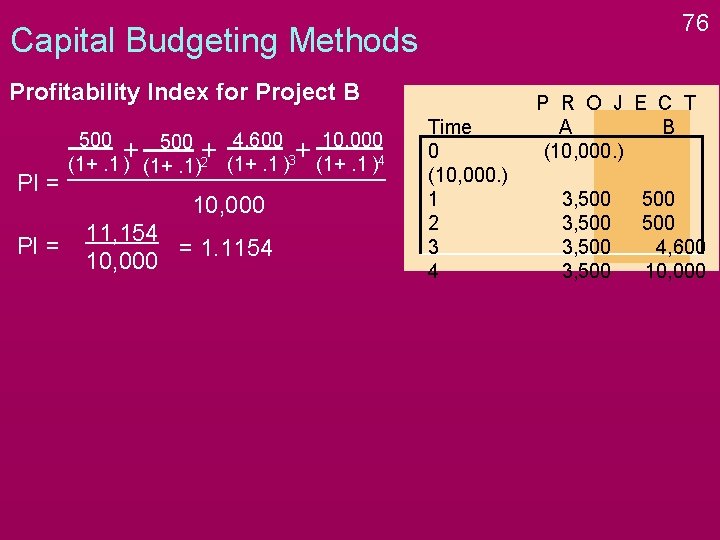
76 Capital Budgeting Methods Profitability Index for Project B PI = 500 4, 600 10, 000 500 + + + (1+. 1 ) (1+. 1)2 (1+. 1 )3 (1+. 1 )4 10, 000 11, 154 = 1. 1154 10, 000 Time 0 (10, 000. ) 1 2 3 4 P R O J E C T A B (10, 000. ) 3, 500 500 4, 600 10, 000

77 Capital Budgeting Methods Profitability Index for Project B PI = 500 4, 600 10, 000 500 + + + (1+. 1 ) (1+. 1)2 (1+. 1 )3 (1+. 1 )4 10, 000 11, 154 = 1. 1154 10, 000 Profitability Index for Project A PI = 3, 500 x PVIFA 4, . 10 10, 000 Time 0 (10, 000. ) 1 2 3 4 P R O J E C T A B (10, 000. ) 3, 500 500 4, 600 10, 000

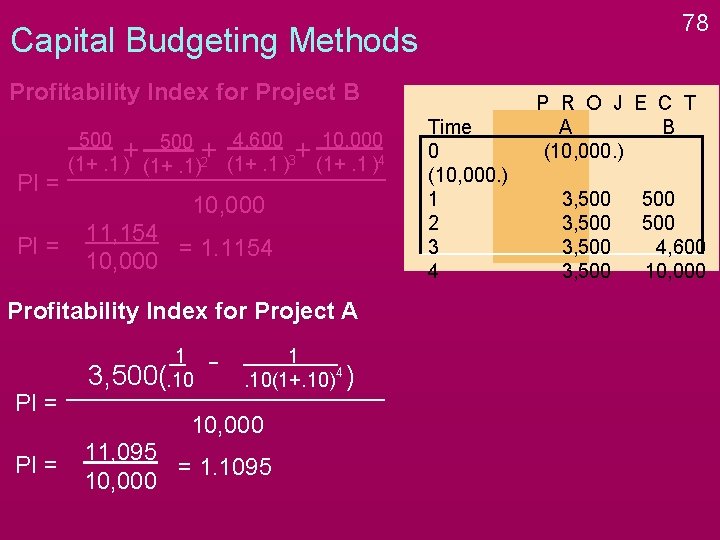
78 Capital Budgeting Methods Profitability Index for Project B PI = 500 4, 600 10, 000 500 + + + (1+. 1 ) (1+. 1)2 (1+. 1 )3 (1+. 1 )4 10, 000 11, 154 = 1. 1154 10, 000 Profitability Index for Project A PI = 1 3, 500(. 10 1 4. 10(1+. 10) ) 10, 000 11, 095 = 1. 1095 10, 000 Time 0 (10, 000. ) 1 2 3 4 P R O J E C T A B (10, 000. ) 3, 500 500 4, 600 10, 000

Capital Budgeting Methods Profitability Index Decision Rules v Independent Projects v. Accept Project if PI ³ 1 v Mutually Exclusive Projects v. Accept Highest PI ³ 1 Project 79

80 Comparison of Methods Project A Payback < 3 years NPV $1, 095 IRR 14. 96% PI 1. 1095 Project B < 4 years $1, 154 13. 50% 1. 1154 Choose A B

Comparison of Methods v Time Value of Money v. Payback - Does not adjust for timing differences (ignore Discounted Payback) v. NPV, IRR and PI take into account the time value of money 81

Comparison of Methods v Time Value of Money v. Payback - Does not adjust for timing differences v. NPV, IRR and PI take into account the time value of money v Relevant Cash Flows? v. NPV, IRR and PI use all Cash Flows v. Payback method ignores Cash Flows that occur after the Payback Period. 82

Comparison of Methods v Time Value of Money v. Payback - Does not adjust for timing differences v. NPV, IRR and PI take into account the time value of money v Relevant Cash Flows? v. NPV, IRR and PI use all Cash Flows v. Payback method ignores Cash Flows that occur after the Payback Period. Project 1 0 1 2 (10, 000) 5, 000 83

84 Comparison of Methods v Time Value of Money v. Payback - Does not adjust for timing differences v. NPV, IRR and PI take into account the time value of money v Relevant Cash Flows? v. NPV, IRR and PI use all Cash Flows v. Payback method ignores Cash Flows that occur after the Payback Period. Project 1 0 1 (10, 000) 5, 000 2 Both Projects have Identical Payback 5, 000 Project 2 0 1 2 3 (10, 000) 5, 000 10, 000

Comparison of Methods NPV & PI indicated accept Project B while IRR indicated that Project A should be accepted. Why? Sometimes there is a conflict between the decisions based on NPV and IRR methods. The conflict arises if there is difference in the timing of CFs or sizes of the projects (or both). The cause of the conflict is the underlying reinvestment rate assumption. Reinvestment Rate Assumptions v. NPV assumes cash flows are reinvested at the required rate, k. v. IRR assumes cash flows are reinvested at IRR. Reinvestment Rate of k more realistic as most projects earn approximately k (due to competition) NPV is the Better Method for project evaluation 85

IRR 86 Because of its unreasonable reinvestment rate assumption, IRR method can result in bad decisions. Another problem with IRR is that if the sign of the cash flow changes more than once, there is a possibility of multiple IRR. See p 340. The problem of unreasonable assumption can be addressed by using Modified IRR

MIRR 87 To find MIRR 1. Find the FV of all intermediate CFs using the cost of capital (the hurdle rate) as the interest rate. 2. Add all FV. 3. Find that discount rate which makes the PV of the FV equal to the PV of outflows. Drop MIRR computations.

88