Anderson Localization and Nonlinearity in OneDimensional Disordered Photonic

Anderson Localization and Nonlinearity in One-Dimensional Disordered Photonic Lattices Yoav Lahini 1, Assaf Avidan 1, Francesca Pozzi 2 , Marc Sorel 2, Roberto Morandotti 3 Demetrios N. Christodoulides 4 and Yaron Silberberg 1 1 Department of Physics of Complex Systems, the Weizmann Institute of Science, Rehovot, Israel of Electrical and Electronic Engineering, University of Glasgow, Scotland 3 Institute National de la Recherché Scientifique, Varennes, Québec, Canada 4 CREOL/College of Optics, University of Central Florida, Orlando, Florida, USA 2 Department www. weizmann. ac. il/~feyaron

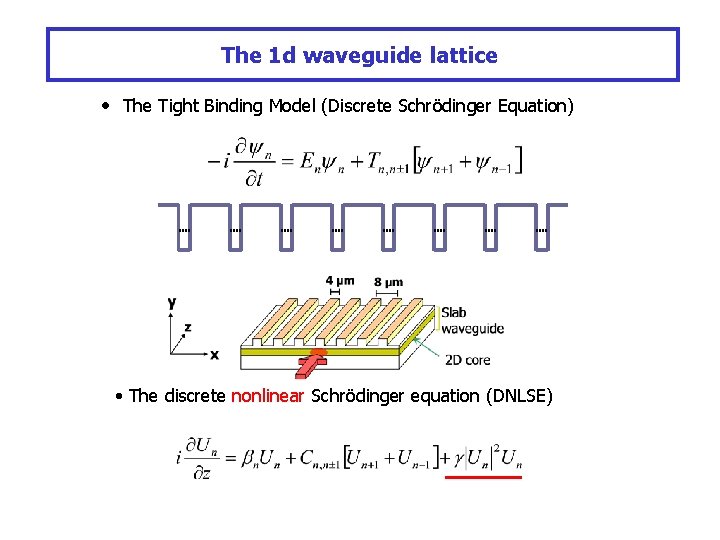
The 1 d waveguide lattice • The Tight Binding Model (Discrete Schrödinger Equation) • The discrete nonlinear Schrödinger equation (DNLSE)

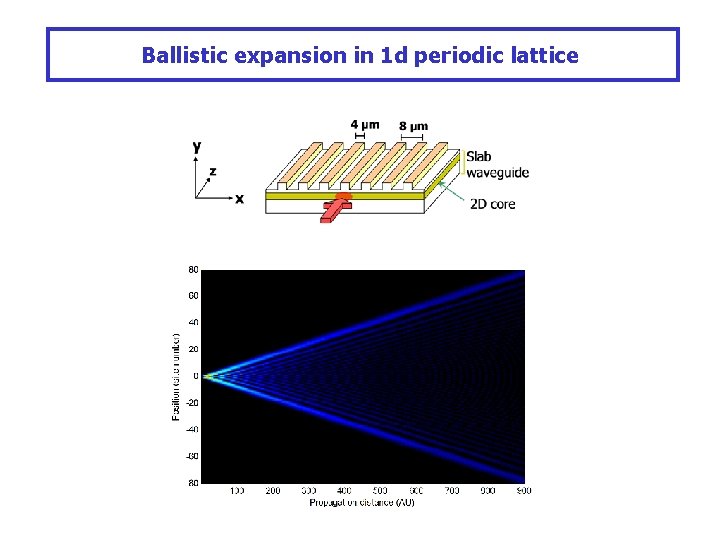
Ballistic expansion in 1 d periodic lattice

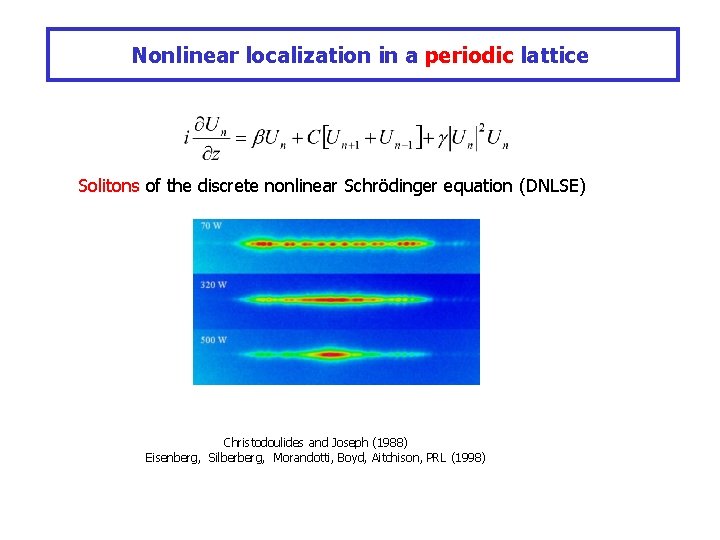
Nonlinear localization in a periodic lattice Solitons of the discrete nonlinear Schrödinger equation (DNLSE) Christodoulides and Joseph (1988) Eisenberg, Silberberg, Morandotti, Boyd, Aitchison, PRL (1998)

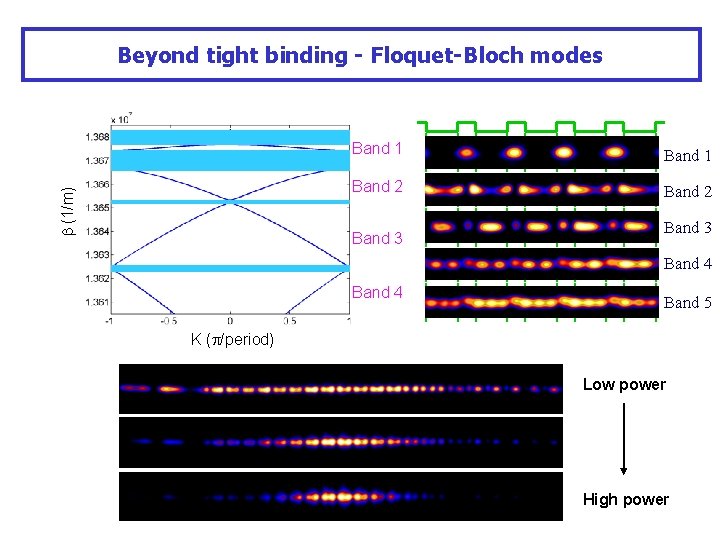
(1/m) Beyond tight binding - Floquet-Bloch modes Band 1 Band 2 Band 3 Band 4 Band 5 K ( /period) Low power High power

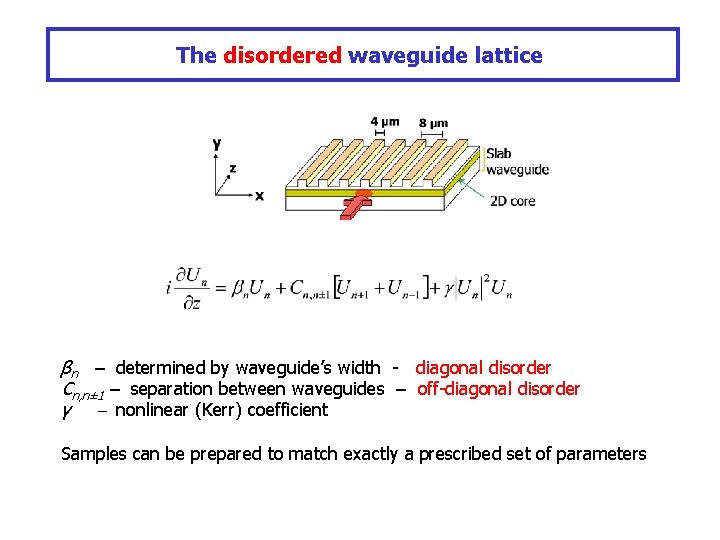
The disordered waveguide lattice βn – determined by waveguide’s width - diagonal disorder Cn, n± 1 – separation between waveguides – off-diagonal disorder γ – nonlinear (Kerr) coefficient Samples can be prepared to match exactly a prescribed set of parameters

In this work 1. Realization of the Anderson model in 1 D 2. An experimental study of the effect of nonlinearity on Anderson localization: • Nonlinearity introduces interactions between propagating waves. This can significantly change interference properties (-> localization). Pikovsky and Shepelyansky: Destruction of Anderson localization by weak nonlinearity Kopidakis et. al. : Absence of Wavepacket Diffusion in Disordered Nonlinear Systems Experiments: Light propagation in nonlinear disordered lattices: Eisenberg, Ph. D. thesis, Weizmann Institute of Science, (2002). (1 D) Pertsch et. al. Phys. Rev. Lett. 93 053901 , (2004). (2 D) Schwartz et. al. Nature 446 53, (2007). (2 D) ar. Xiv: 0708. 3315 (2007) ar. Xiv: 0710. 2621 (2007)

The Original Anderson Model in 1 D • The discrete Schrödinger equation (Tight Binding model) • The Anderson model: • A measure of disorder is given by P. W. Anderson, Phys. Rev. 109 1492 (1958) Flat distribution, width Δ

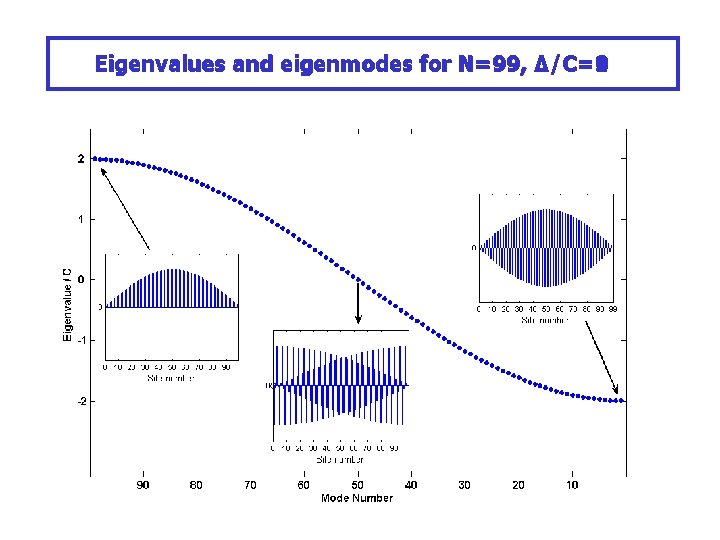
Eigenmodes of a periodic lattice N=99

Δ/C=0 Eigenvalues and eigenmodes for N=99, Δ/C=1 Δ/C=3

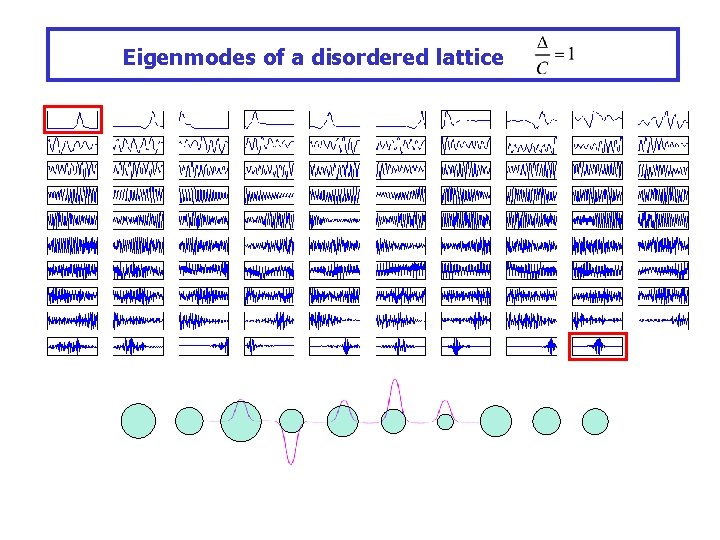
Eigenmodes of a disordered lattice

Eigenmodes of a disordered lattice N=99, Δ/C=1 : Intensity distributions

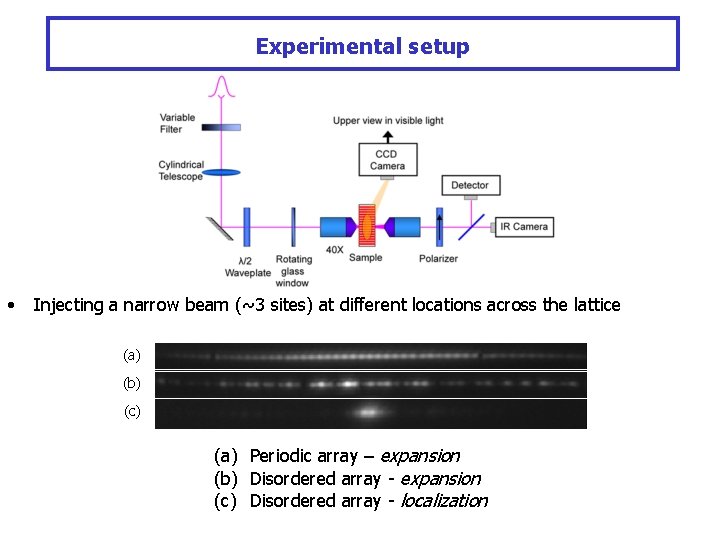
Experimental setup • Injecting a narrow beam (~3 sites) at different locations across the lattice (a) (b) (c) (a) Periodic array – expansion (b) Disordered array - expansion (c) Disordered array - localization

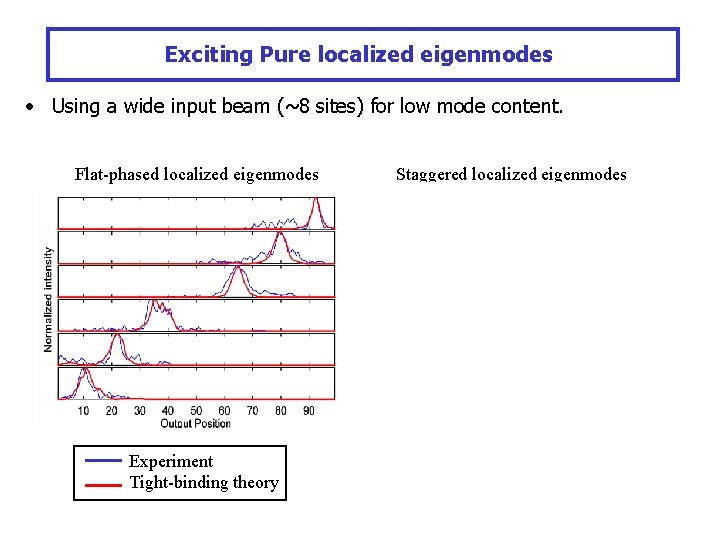
Exciting Pure localized eigenmodes • Using a wide input beam (~8 sites) for low mode content. Flat-phased localized eigenmodes Experiment Tight-binding theory Staggered localized eigenmodes

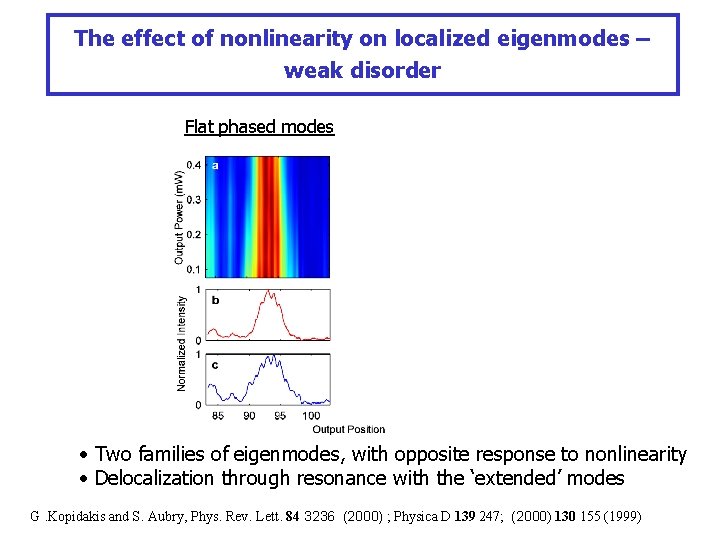
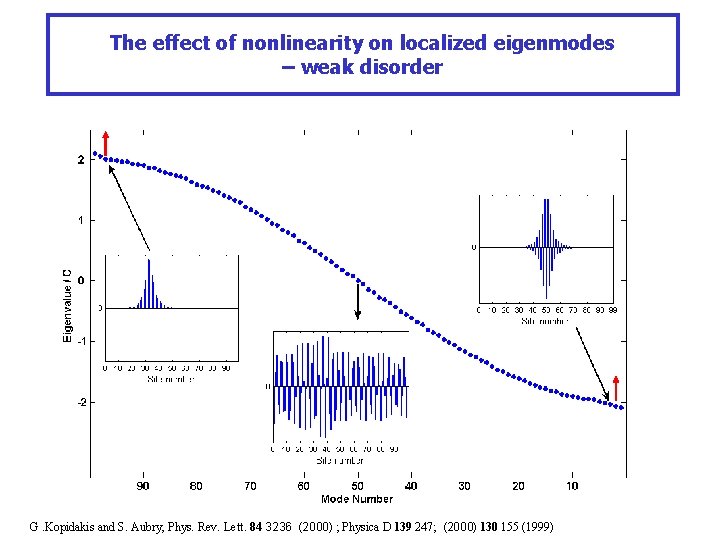
The effect of nonlinearity on localized eigenmodes – weak disorder Flat phased modes Staggered modes • Two families of eigenmodes, with opposite response to nonlinearity • Delocalization through resonance with the ‘extended’ modes G. Kopidakis and S. Aubry, Phys. Rev. Lett. 84 3236 (2000) ; Physica D 139 247; (2000) 130 155 (1999)

The effect of nonlinearity on localized eigenmodes – weak disorder G. Kopidakis and S. Aubry, Phys. Rev. Lett. 84 3236 (2000) ; Physica D 139 247; (2000) 130 155 (1999)

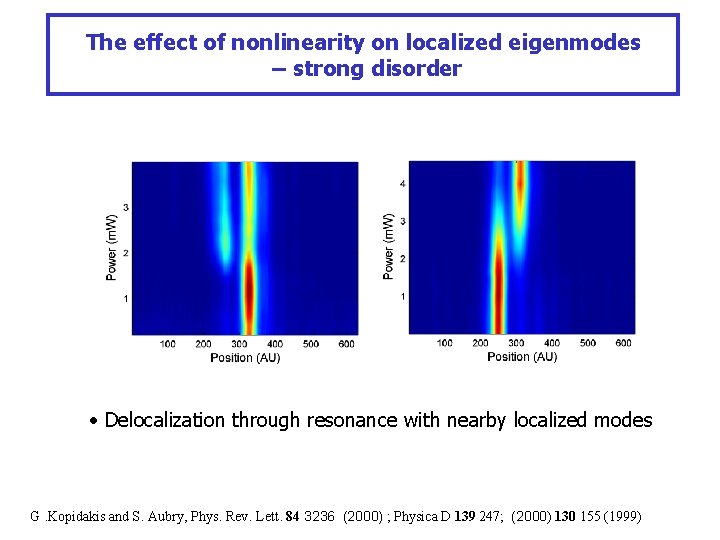
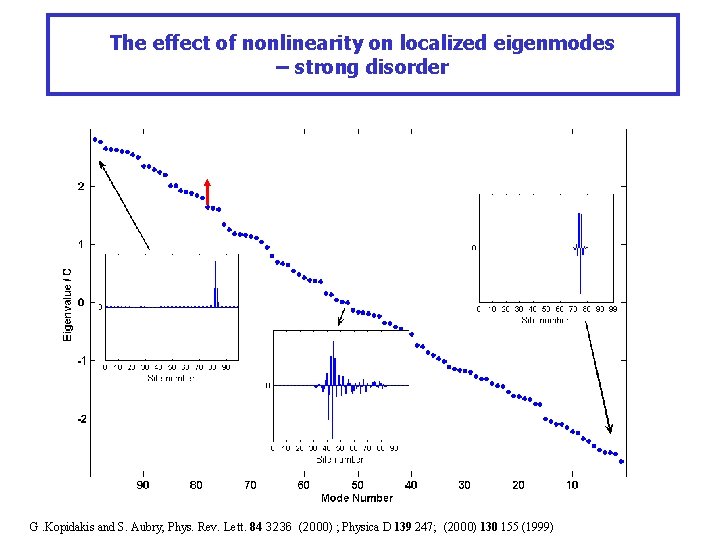
The effect of nonlinearity on localized eigenmodes – strong disorder • Delocalization through resonance with nearby localized modes G. Kopidakis and S. Aubry, Phys. Rev. Lett. 84 3236 (2000) ; Physica D 139 247; (2000) 130 155 (1999)

The effect of nonlinearity on localized eigenmodes – strong disorder G. Kopidakis and S. Aubry, Phys. Rev. Lett. 84 3236 (2000) ; Physica D 139 247; (2000) 130 155 (1999)

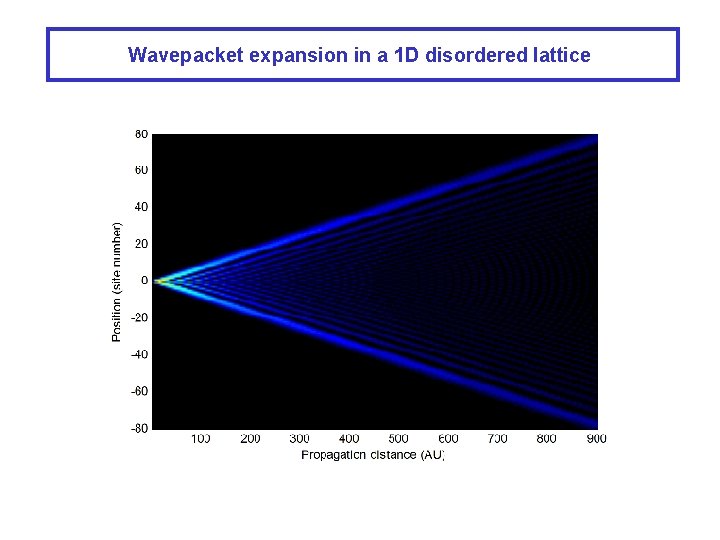
Wavepacket expansion in disordered lattices The effect of nonlinearity on wavepacket expansion • • Single-site excitation Short time behavior – from ballistic expansion to localization

Wavepacket expansion in a 1 D disordered lattice

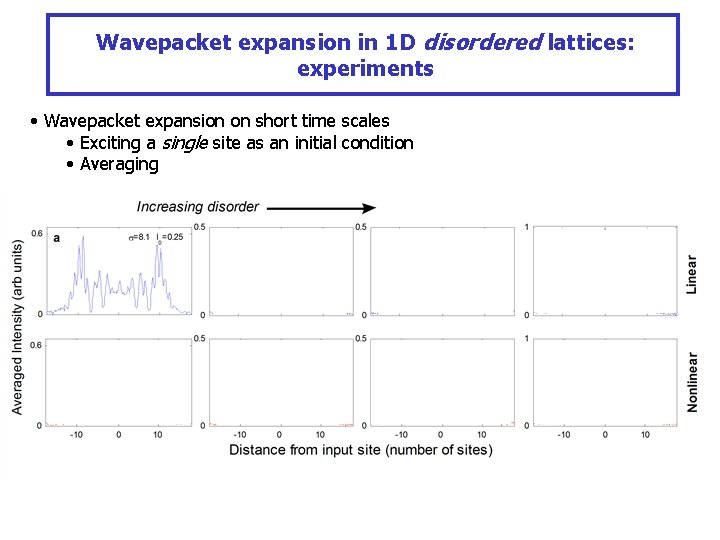
Wavepacket expansion in 1 D disordered lattices: experiments • Wavepacket expansion on short time scales • Exciting a single site as an initial condition • Averaging

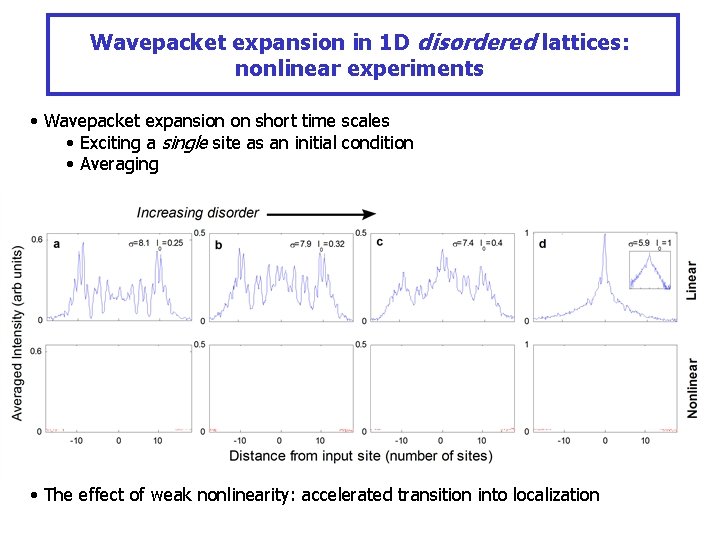
Wavepacket expansion in 1 D disordered lattices: nonlinear experiments • Wavepacket expansion on short time scales • Exciting a single site as an initial condition • Averaging • The effect of weak nonlinearity: accelerated transition into localization

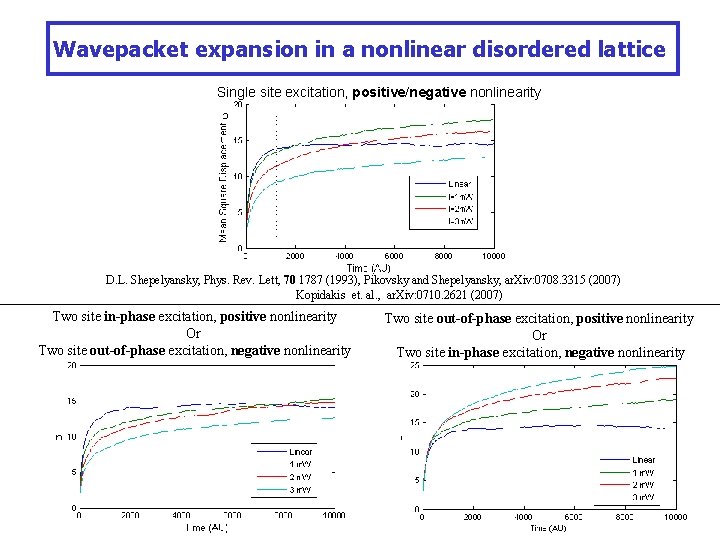
Wavepacket expansion in a nonlinear disordered lattice Single site excitation, positive/negative nonlinearity D. L. Shepelyansky, Phys. Rev. Lett, 70 1787 (1993), Pikovsky and Shepelyansky, ar. Xiv: 0708. 3315 (2007) Kopidakis et. al. , ar. Xiv: 0710. 2621 (2007) Two site in-phase excitation, positive nonlinearity Or Two site out-of-phase excitation, negative nonlinearity Two site out-of-phase excitation, positive nonlinearity Or Two site in-phase excitation, negative nonlinearity

Summary • • • Realization of the 1 D Anderson model with nonlinearity. Full control over all disorder parameters. Selective excitation of localized eigenmodes. The effect of nonlinearity on eigenmodes in the weak and strong disorder regimes. Wavepacket expansion in 1 D disordered lattices: the buildup of localization – co-existence of a ballistic and localized component – no diffusive dynamics in 1 D Effect of (weak) nonlinearity on wavepacket expansion in disordered lattices: an accelerated buildup of localization