Localization Murat Demirbas SUNY Buffalo Localization Localization of

Localization Murat Demirbas SUNY Buffalo

Localization • Localization of a node refers to the problem of identifying its spatial co-ordinates in some co-ordinate system ¾ How do nodes discover their geographic positions in 2 D or 3 D space? • Model: static wireless sensor networks 2

Location Matters • Sensor Net Applications ¾ Environment monitoring ¾ Event tracking ¾ Smart environment • Geographic routing protocols ¾ Geo. Cast, GPSR, LAR, GAF, GEAR 3

Outline • Range-based localization ¾ GPS ¾ Cricket ¾ APS ¾ RADAR • Range-free localization ¾ Centroid ¾ DV-HOP ¾ APIT 4

Range-based localization Distances between nodes to nodes/anchors measured wirelessly • TOA (Time of Arrival ) ¾ GPS • TDOA (Time Difference of Arrival) ¾ Cricket • AOA (Angle of Arrive ) ¾ APS • RSSI (Receive Signal Strength Indicator) ¾ RADAR 5

Outline • Range-based localization ¾ GPS ¾ Cricket ¾ APS ¾ RADAR • Range-free localization ¾ Centroid ¾ DV-HOP ¾ APIT 6

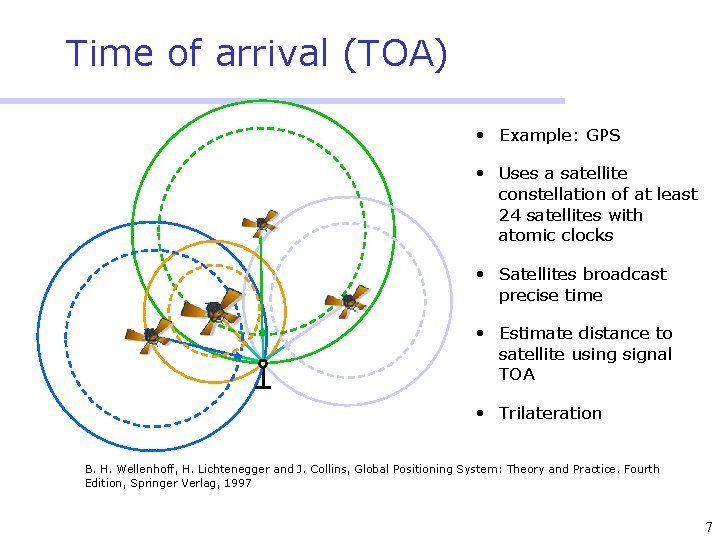
Time of arrival (TOA) • Example: GPS • Uses a satellite constellation of at least 24 satellites with atomic clocks • Satellites broadcast precise time • Estimate distance to satellite using signal TOA • Trilateration B. H. Wellenhoff, H. Lichtenegger and J. Collins, Global Positioning System: Theory and Practice. Fourth Edition, Springer Verlag, 1997 7

Outline • Range-based localization ¾ GPS ¾ Cricket ¾ APS ¾ RADAR • Range-free localization ¾ Centroid ¾ DV-HOP ¾ APIT 8

Sound based To. F approach Because the speed of sound is much slower (approximately 331. 4 m/s) than radio, it is easier to be applied in sensor network. Some hurdles are: • Line of sight path must exist between sender and receiver. • Mono-direction. • Short range. 9

Cricket • Intended for indoors use where GPS don't work • It can provide distance ranging and positioning precision of between 1 and 3 cm • Active beacons and passive listeners 10

Outline • Range-based localization ¾ GPS ¾ Cricket ¾ APS ¾ RADAR • Range-free localization ¾ Centroid ¾ DV-HOP ¾ APIT 11

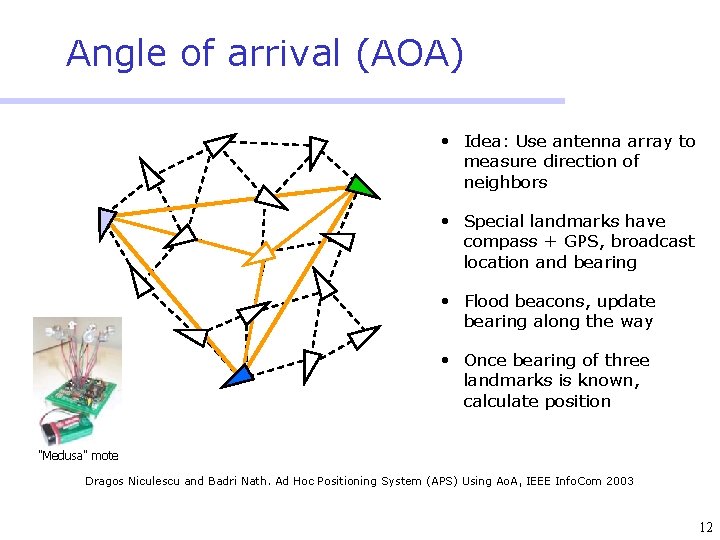
Angle of arrival (AOA) • Idea: Use antenna array to measure direction of neighbors • Special landmarks have compass + GPS, broadcast location and bearing • Flood beacons, update bearing along the way • Once bearing of three landmarks is known, calculate position "Medusa" mote Dragos Niculescu and Badri Nath. Ad Hoc Positioning System (APS) Using Ao. A, IEEE Info. Com 2003 12

Outline • Range-based localization ¾ GPS ¾ Cricket ¾ APS ¾ RADAR • Range-free localization ¾ Centroid ¾ DV-HOP ¾ APIT 13

RADAR • Bahl: MS research • Offline calibration: ¾ Tabulate <location, RSSI> to construct radio map • Real-time location & tracking: ¾ Extract RSSI from base station beacons ¾ Find table entry best matching the measurement 14

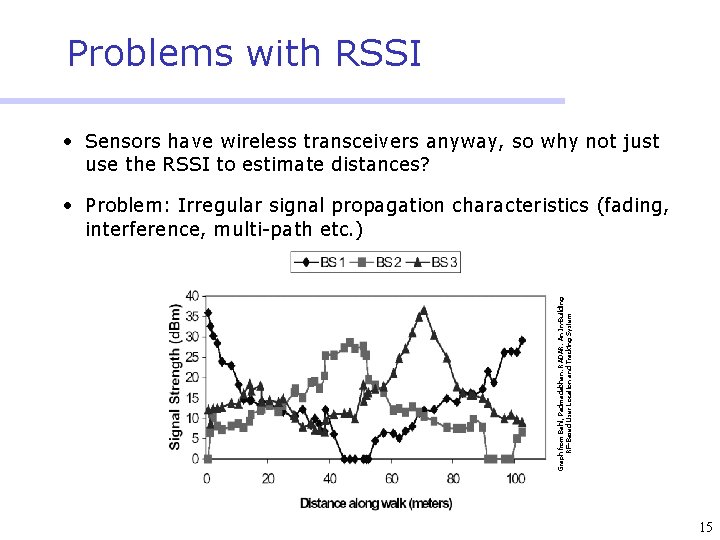
Problems with RSSI • Sensors have wireless transceivers anyway, so why not just use the RSSI to estimate distances? Graph from Bahl, Padmadabhan: RADAR: An In-Building RF-Based User Location and Tracking System • Problem: Irregular signal propagation characteristics (fading, interference, multi-path etc. ) 15

Outline • Range-based localization ¾ GPS ¾ Cricket ¾ APS ¾ RADAR • Range-free localization ¾ Centroid ¾ DV-HOP ¾ APIT 16

Range-free localization Range-based localization: ¾ Required Expensive hardware ¾ Limited working range ( Dense anchor requirement) Range-free localization: ¾ Simple hardware ¾ Less accuracy 17

Outline • Range-based localization ¾ GPS ¾ Cricket ¾ APS ¾ RADAR • Range-free localization ¾ Centroid ¾ DV-HOP ¾ APIT 18

Range-free: Centroid • Idea: Do not use any ranging at all, simply deploy enough beacons • Anchors periodically broadcast their location Anchors • Localization: ¾ Listen for beacons ¾ Average locations of all anchors in range ¾ Result is location estimate • Good anchor placement is crucial! Nirupama Bulusu, John Heidemann and Deborah Estrin. Density Adaptive Beacon Placement, Proceedings of the 21 st IEEE ICDCS, 2001 19

Outline • Range-based localization ¾ GPS ¾ Cricket ¾ APS ¾ RADAR • Range-free localization ¾ Centroid ¾ DV-HOP ¾ APIT 20

Hop-Count Techniques r 4 1 2 3 1 3 4 4 5 2 3 7 4 3 8 6 DV-HOP [Niculescu & Nath, 2003] Amorphous [Nagpal et. al, 2003] 4 5 Works well with a few, well-located seeds and regular, static node distribution. Works poorly if nodes move or are unevenly distributed. 21

Outline • Range-based localization ¾ GPS ¾ Cricket ¾ APS ¾ RADAR • Range-free localization ¾ Centroid ¾ DV-HOP ¾ APIT 22

Overview of APIT • APIT employs a novel areabased approach. Anchors divide terrain into triangular regions • A node’s presence inside or outside of these triangular regions allows a node to narrow the area in which it can potentially reside. • The method to do so is called Approximate Point In Triangle Test (APIT). 23

Algorithm • Anchor Beaconing • Individual APIT Test Pseudo Code: Receive beacons (Xi, Yi) from N anchors • Triangle Aggregation N anchors form • Center of Gravity Estimation For ( each triangle Ti Є triangles. ){ Inside. Set Point-In-Triangle. Test (Ti) } Position = COG ( ∩Ti Inside. Set); 24

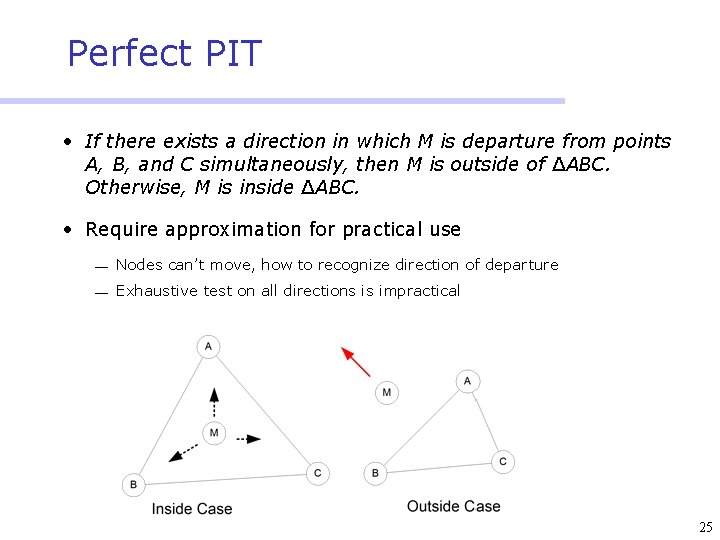
Perfect PIT • If there exists a direction in which M is departure from points A, B, and C simultaneously, then M is outside of ∆ABC. Otherwise, M is inside ∆ABC. • Require approximation for practical use ¾ Nodes can’t move, how to recognize direction of departure ¾ Exhaustive test on all directions is impractical 25

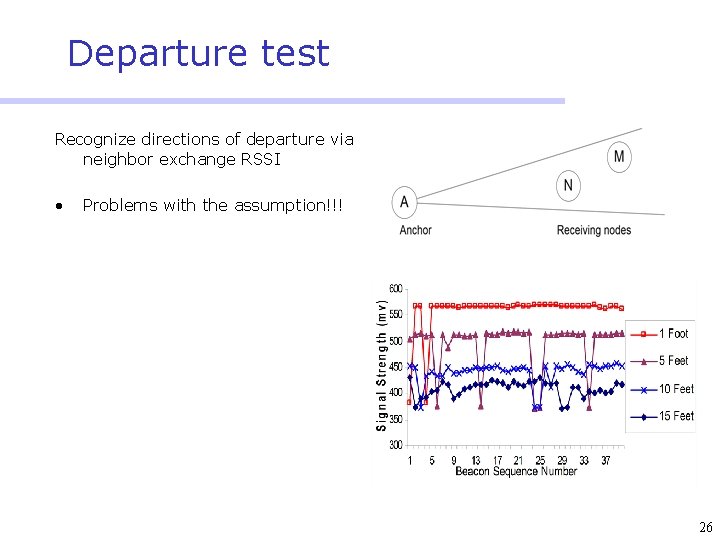
Departure test Recognize directions of departure via neighbor exchange RSSI • Problems with the assumption!!! 26

APIT approximation Test only directions towards neighbors ¾ Error in individual test exists, may be masked by APIT aggregation. 27

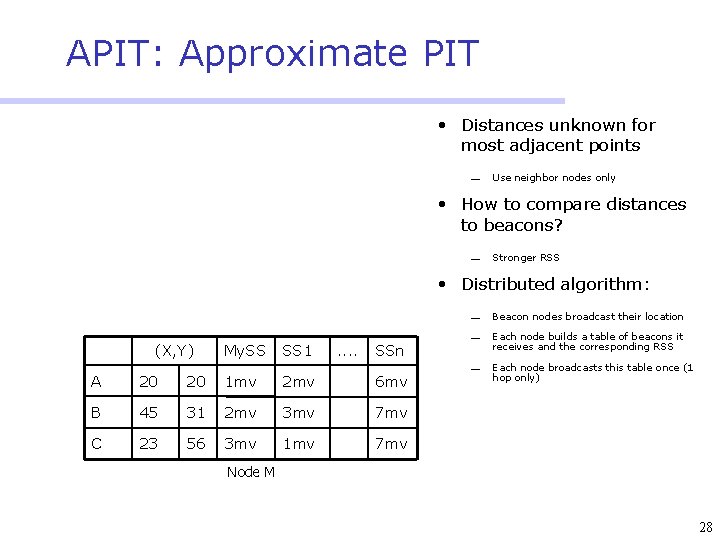
APIT: Approximate PIT • Distances unknown for most adjacent points ¾ Use neighbor nodes only • How to compare distances to beacons? ¾ Stronger RSS • Distributed algorithm: (X, Y) My. SS SS 1 . . SSn A 20 20 1 mv 2 mv 6 mv B 45 31 2 mv 3 mv 7 mv C 23 56 3 mv 1 mv 7 mv ¾ Beacon nodes broadcast their location ¾ Each node builds a table of beacons it receives and the corresponding RSS ¾ Each node broadcasts this table once (1 hop only) Node M 28

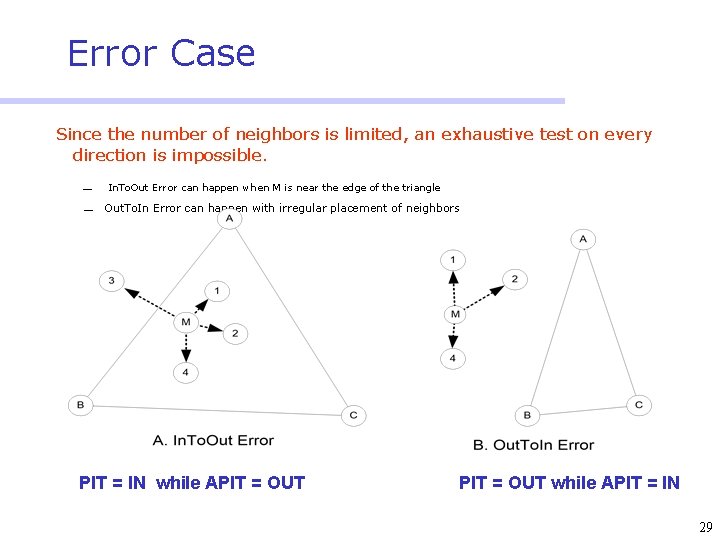
Error Case Since the number of neighbors is limited, an exhaustive test on every direction is impossible. ¾ ¾ In. To. Out Error can happen when M is near the edge of the triangle Out. To. In Error can happen with irregular placement of neighbors PIT = IN while APIT = OUT while APIT = IN 29

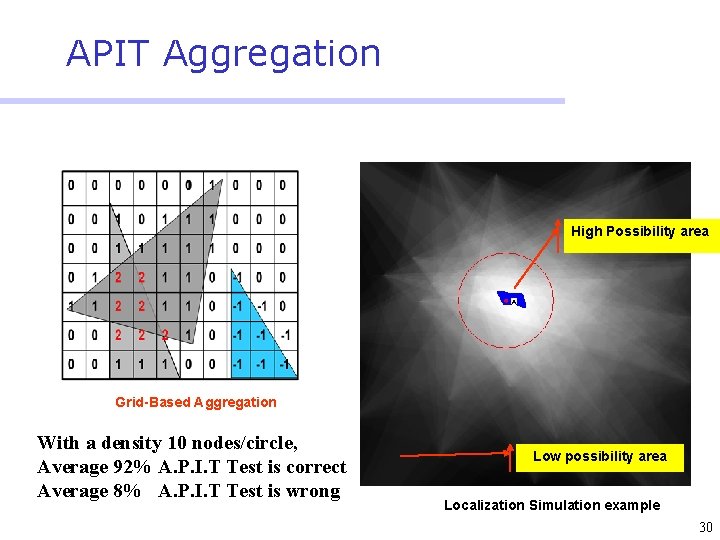
APIT Aggregation High Possibility area Grid-Based Aggregation With a density 10 nodes/circle, Average 92% A. P. I. T Test is correct Average 8% A. P. I. T Test is wrong Low possibility area Localization Simulation example 30

Evaluation • Radio Model: Continuous Radio Variation Model. – Degree of Irregularity (DOI ) is defined as maximum radio range variation per unit degree change in the direction of radio propagation α DOI =0 DOI = 0. 05 DOI = 0. 2 31

Simulation Setup • Setup ¾ 1000 by 1000 m area ¾ 2000 ~ 4000 nodes ( random or uniform placement ) ¾ 10 to 30 anchors ( random or uniform placement ) ¾ Node density: 6 ~ 20 node/ radio range ¾ Anchor percentage 0. 5~2% ¾ 90% confidence intervals are within in 5~10% of the mean • Metrics ¾ Localization Estimation Error ( normalized to units of radio range) ¾ Communication Overhead in terms of #message 32

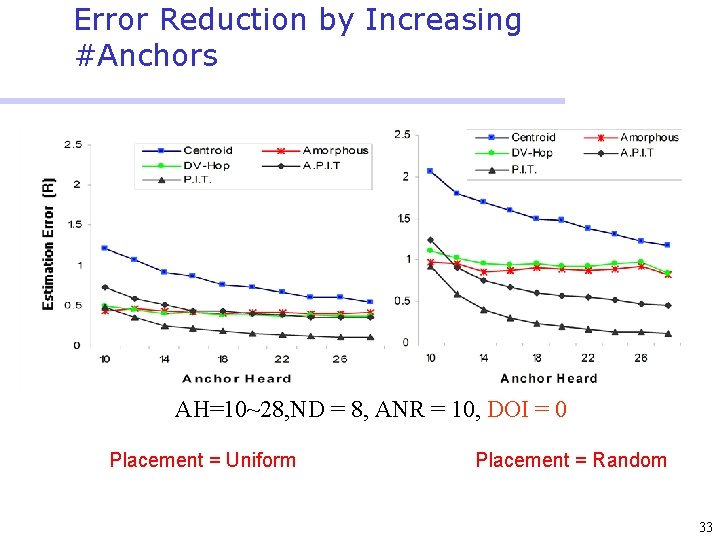
Error Reduction by Increasing #Anchors AH=10~28, ND = 8, ANR = 10, DOI = 0 Placement = Uniform Placement = Random 33

Error Reduction by Increasing Node Density AH=16, Uniform, AP = 0. 6%~2%, ANR = 10 DOI=0. 1 DOI=0. 2 34

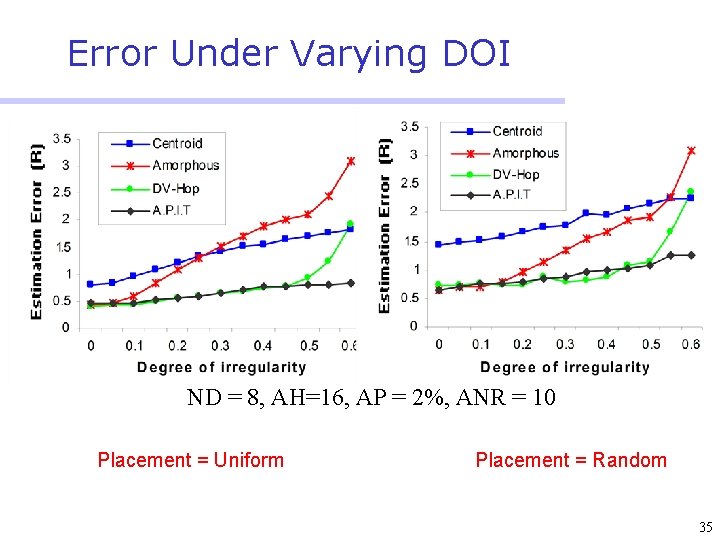
Error Under Varying DOI ND = 8, AH=16, AP = 2%, ANR = 10 Placement = Uniform Placement = Random 35

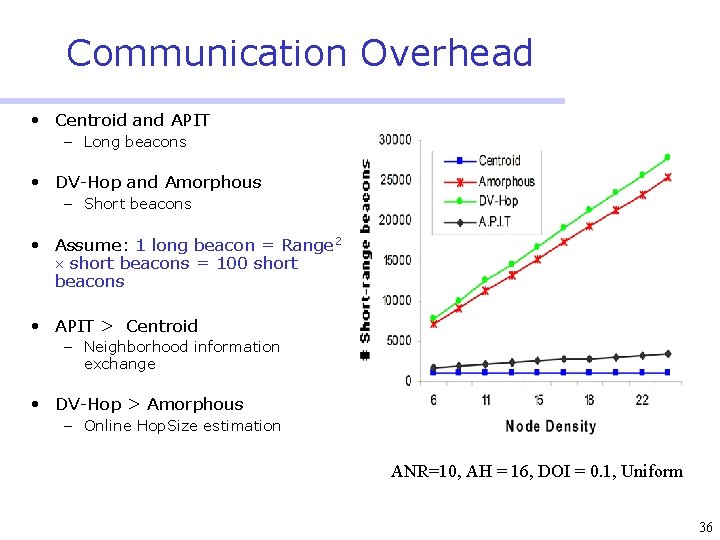
Communication Overhead • Centroid and APIT – Long beacons • DV-Hop and Amorphous – Short beacons • Assume: 1 long beacon = Range 2 short beacons = 100 short beacons • APIT > Centroid – Neighborhood information exchange • DV-Hop > Amorphous – Online Hop. Size estimation ANR=10, AH = 16, DOI = 0. 1, Uniform 36

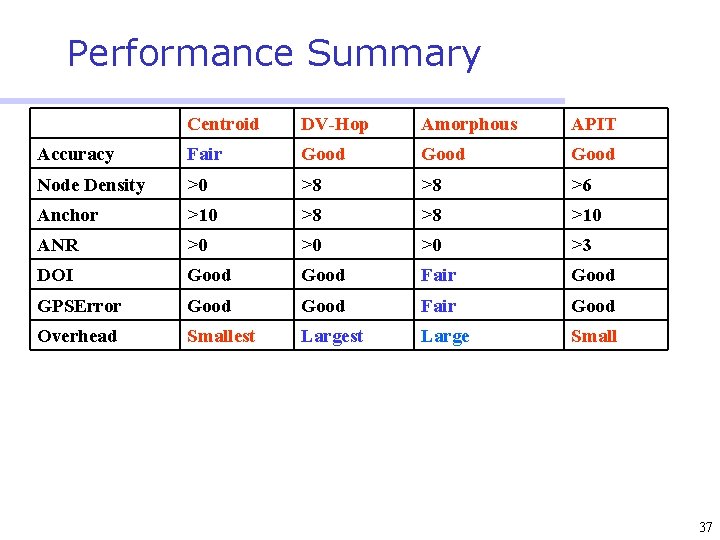
Performance Summary Centroid DV-Hop Amorphous APIT Accuracy Fair Good Node Density >0 >8 >8 >6 Anchor >10 >8 >8 >10 ANR >0 >0 >0 >3 DOI Good Fair Good GPSError Good Fair Good Overhead Smallest Large Small 37