Analyzing error of fit functions for ellipses Paul

Analyzing error of fit functions for ellipses Paul L. Rosin BMVC 1996

Why? • Ellipse fitting to pupil boundary • RANSAC Pupil edge pixels (Random sample consensus) – Explore fits – Select best fit • Selection based on error criterion Noise pixels

Overview • Ellipse Error of fit (EOF) functions – How far is a point from ellipse boundary? – Approx. to Euclidean dist (hard to compute!) – Ellipse fitting using Least Squares (LS) X 6 e 6 X 1 • Evaluation X 5 e 1 X 2 e 2 X 3 X 4 e 3 – Linearity, Curvature bias, Asymmetry

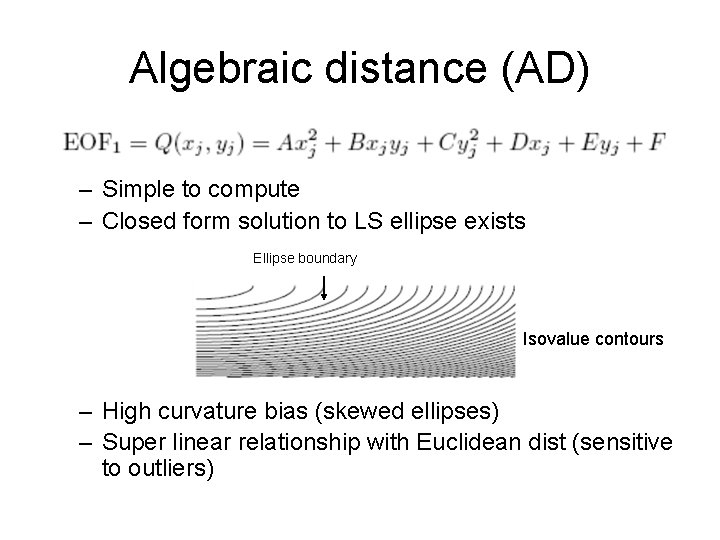
Algebraic distance (AD) – Simple to compute – Closed form solution to LS ellipse exists Ellipse boundary Isovalue contours – High curvature bias (skewed ellipses) – Super linear relationship with Euclidean dist (sensitive to outliers)

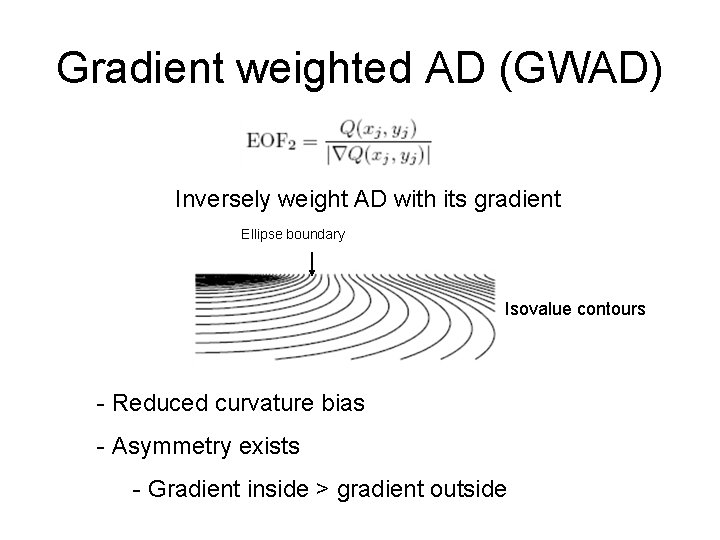
Gradient weighted AD (GWAD) Inversely weight AD with its gradient Ellipse boundary Isovalue contours - Reduced curvature bias - Asymmetry exists - Gradient inside > gradient outside

Second order approximation Ellipse boundary Isovalue contours – Does not exist for points near high curvature sections

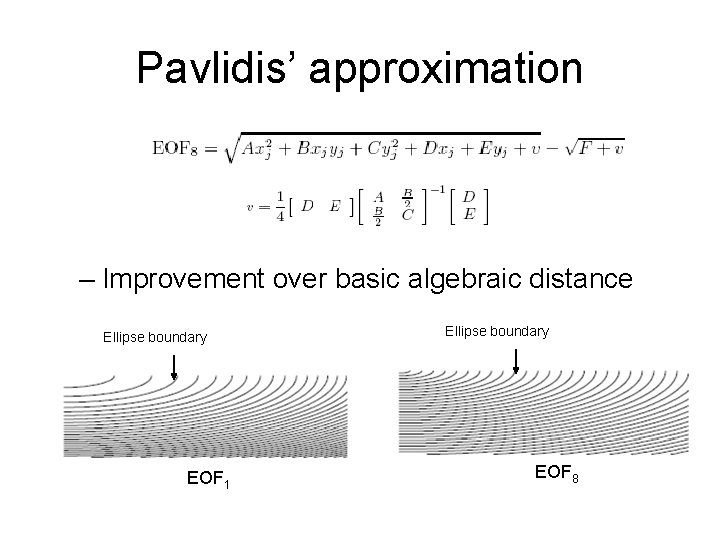
Pavlidis’ approximation – Improvement over basic algebraic distance Ellipse boundary EOF 1 Ellipse boundary EOF 8

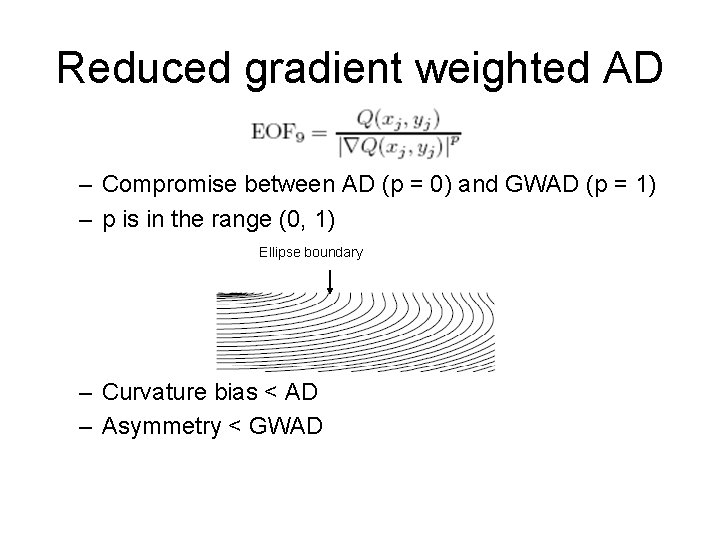
Reduced gradient weighted AD – Compromise between AD (p = 0) and GWAD (p = 1) – p is in the range (0, 1) Ellipse boundary – Curvature bias < AD – Asymmetry < GWAD

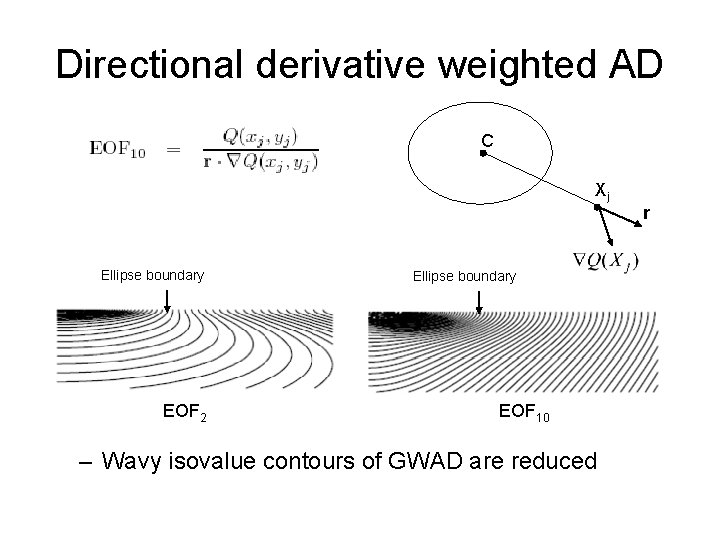
Directional derivative weighted AD C Xj Ellipse boundary EOF 2 Ellipse boundary EOF 10 – Wavy isovalue contours of GWAD are reduced r

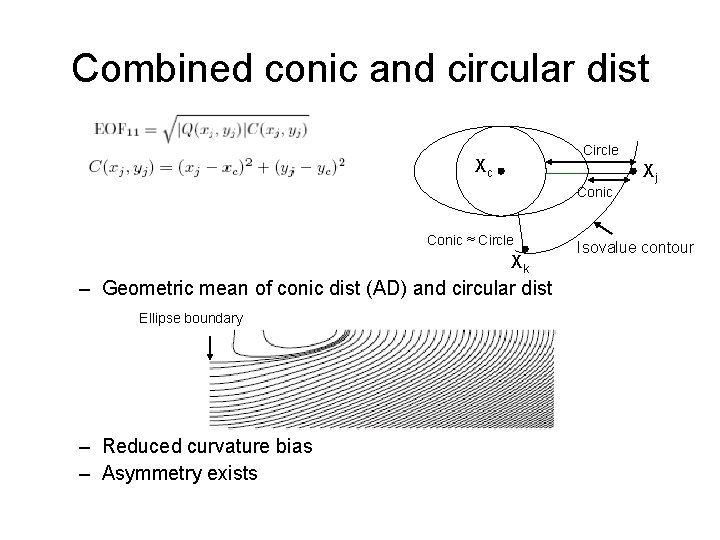
Combined conic and circular dist Circle Xc Xj Conic ≈ Circle Xk – Geometric mean of conic dist (AD) and circular dist Ellipse boundary – Reduced curvature bias – Asymmetry exists Isovalue contour

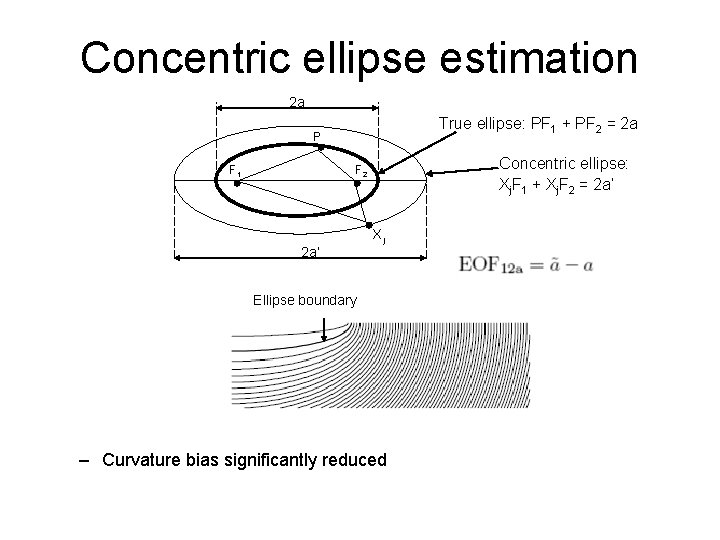
Concentric ellipse estimation 2 a True ellipse: PF 1 + PF 2 = 2 a P F 1 Concentric ellipse: Xj. F 1 + Xj. F 2 = 2 a’ F 2 2 a’ Xj Ellipse boundary – Curvature bias significantly reduced

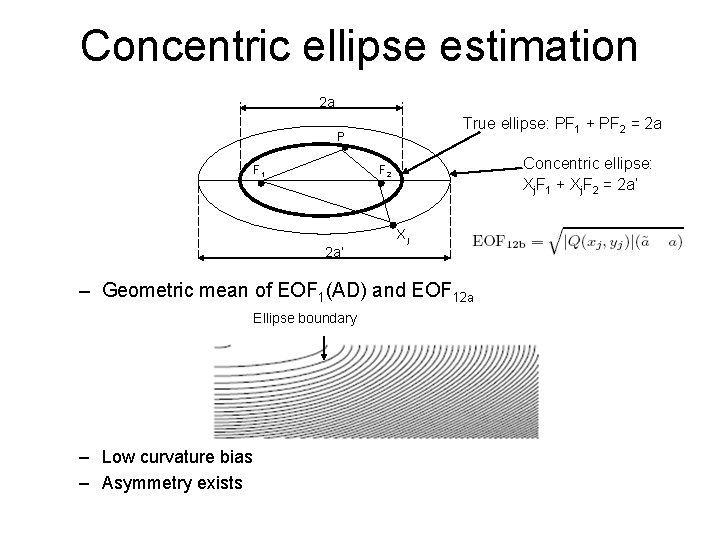
Concentric ellipse estimation 2 a True ellipse: PF 1 + PF 2 = 2 a P F 1 Concentric ellipse: Xj. F 1 + Xj. F 2 = 2 a’ F 2 2 a’ Xj – Geometric mean of EOF 1(AD) and EOF 12 a Ellipse boundary – Low curvature bias – Asymmetry exists

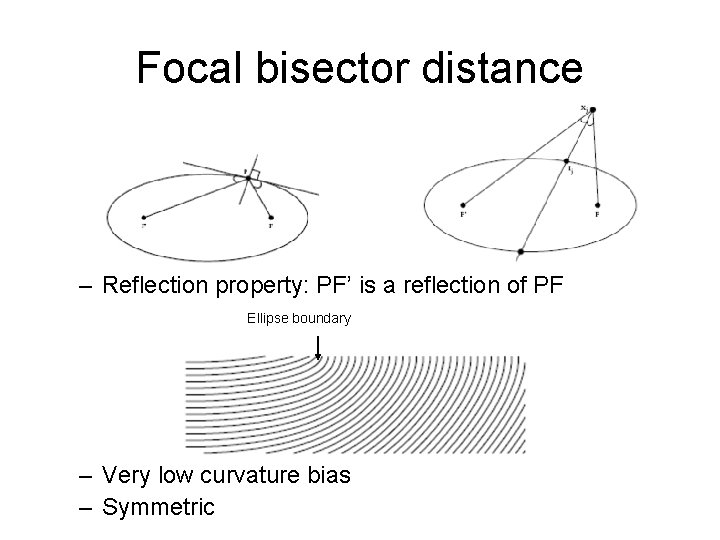
Focal bisector distance – Reflection property: PF’ is a reflection of PF Ellipse boundary – Very low curvature bias – Symmetric

Radial distance T EOF 5 = Xj. T C – Comparison with focal bisector distance Ellipse boundary EOF 5 = Xj. T EOF 13 = Xj. Ij

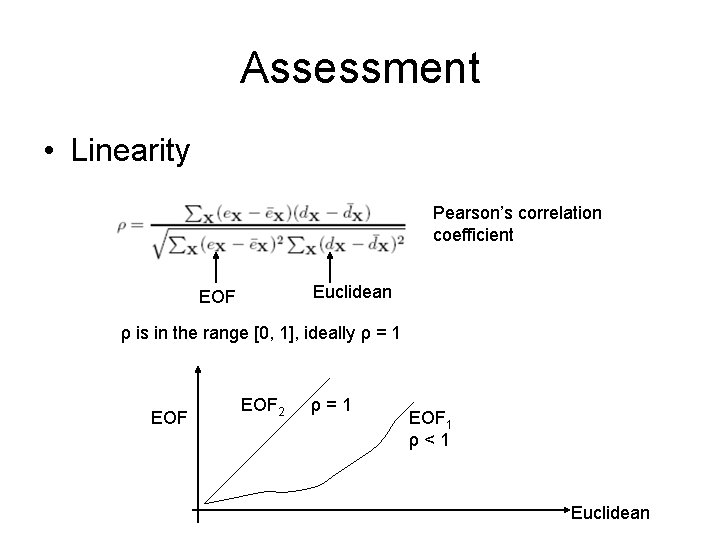
Assessment • Linearity Pearson’s correlation coefficient Euclidean EOF ρ is in the range [0, 1], ideally ρ = 1 EOF 2 ρ=1 EOF 1 ρ<1 Euclidean

Assessment • Linearity – Points on farther isovalue contours contribute more – Farther isovalue contours are longer Mean euclidean distance along an isovalue contour at Ei Modified Pearson’s correlation coefficient (more uniform sampling) Gaussian weighting according to distance d from ellipse boundary

Assessment • Curvature bias Local variation of euclidean distance along an isovalue contour at Ei Global curvature measure considering all isovalue contours Ei Low values of C imply low curvature bias, ideally C = 0

Assessment • Asymmetry Mean of euclidean distance along an outside isovalue contour at Ei Mean of euclidean distance along an inside isovalue contour at Ei Local assymetry w. r. t. isovalue contour at Ei Global assymetry measure considering all isovalue contours Ei Low values of A imply low asymmetry, ideally A = 0

Assessment • Combined measure – Overall goodness Weighted sum of square errors between euclidean distance and scaled EOF Global scaling factor S is determined by optimizing G

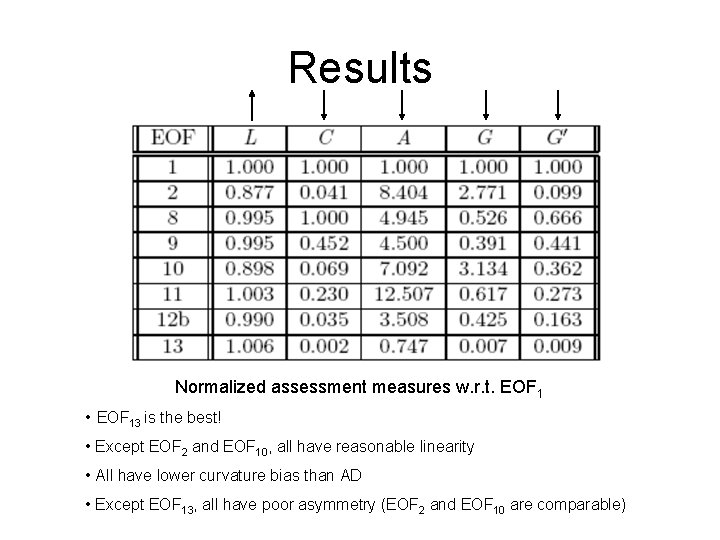
Results Normalized assessment measures w. r. t. EOF 1 • EOF 13 is the best! • Except EOF 2 and EOF 10, all have reasonable linearity • All have lower curvature bias than AD • Except EOF 13, all have poor asymmetry (EOF 2 and EOF 10 are comparable)

Our work • RANSAC consensus (selection) – Algebraic dist vs. Focal bisector dist Selection using algebraic distance Selection using focal bisector distance

Thank you!!