Analisi e Sintesi di circuiti sequenziali Definizione Una

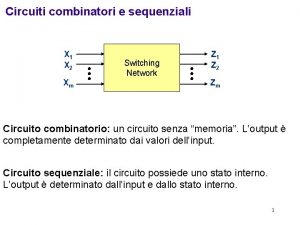
Analisi e Sintesi di circuiti sequenziali

Definizione • Una macchina sequenziale é un sistema nel quale, detto • I(t) l'insieme degli ingressi in t, O(t) l'insieme delle uscite in t, e M(t) una funzione di • I(t-1), I(t-2). . . (i=1, . . n) detta memoria, si ha: • oi(t)=F(I(t), M(t)) , oiÎ O

Automi a stati finiti Un automa a stati finiti é una quintupla (Q, S, d, q 0, F) dove Q e' un insieme finito di stati, S e' un alfabeto finito di simboli, q 0 e' lo stato iniziale, F Í Q e' il set di stati finali, e � e' la funzione di transizione Qx. S --> Q ( Qx S e' il prodotto cartesiano, ovvero l'insieme delle coppie q, a ); d(q, a) rappresenta uno stato raggiunto dall'automa, per ogni stato di partenza q e simbolo di ingresso a.

Rappresentazione tabellare • Alternativamente, un automa si può rappresentare mediante una tabella delle transizioni, o stati futuri: •

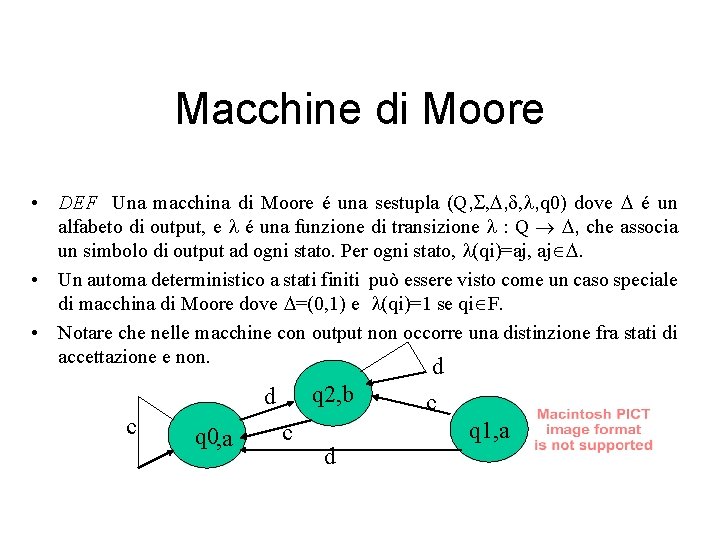
Macchine di Moore • DEF Una macchina di Moore é una sestupla (Q, S, D, d, l, q 0) dove D é un alfabeto di output, e l é una funzione di transizione l : Q D, che associa un simbolo di output ad ogni stato. Per ogni stato, l(qi)=aj, ajÎD. • Un automa deterministico a stati finiti può essere visto come un caso speciale di macchina di Moore dove D=(0, 1) e l(qi)=1 se qiÎF. • Notare che nelle macchine con output non occorre una distinzione fra stati di accettazione e non. d q 2, b d c q 0, a c d c q 1, a

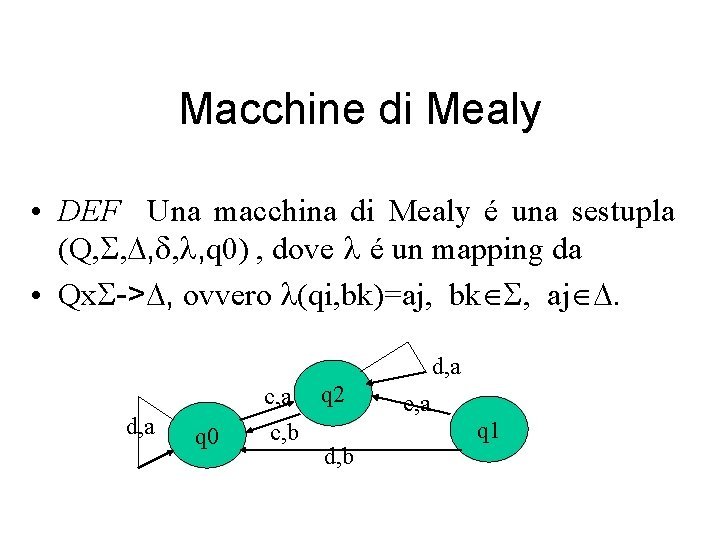
Macchine di Mealy • DEF Una macchina di Mealy é una sestupla (Q, S, D, d, l, q 0) , dove l é un mapping da • Qx. S->D, ovvero l(qi, bk)=aj, bkÎS, ajÎD. d, a q 0 c, a q 2 c, b d, b c, a q 1

Equivalenza fra macchine di Moore e Mealy • Teorema. Se M 1= (Q, S, D, d, l, q 0) é una macchina di Moore, allora esiste una macchina di Mealy equivalente M 2. • Dimostrazione. sia M 2=(Q, S, D, d, l', q 0) e definiamo: l'(q, a)=l(d(q, a)) • Allora, M 2 è equivalente a M 1 e segue le stesse transizioni, emettendo ad ogni transizione l'output associato allo stato di arrivo in M 1.

Equivalenza Mealy Moore • Teorema. Se M 1= (Q, S, D, d, l, q 0) é una macchina di Mealy, allora esiste una macchina di Moore equivalente M 2. • Dimostrazione. sia M 2=(Qx. D, S, D, d', l', (q 0 b 0)), dove b 0 é un qualsiasi carattere di D. Gli stati M 2 sono coppie rappresentate da stati di M 1 e simboli di D. Definiamo d'((q, b), a) = (d(q, a), l(q, a)) e l'((q, b))=b • I due automi sono equivalenti, infatti le transizioni di M 2 da uno stato all'altro sono determinate solo dal primo elemento della coppia che identifica lo stato, e dal valore dell'input. Ovvero, da uno stato (q, b), quando si riceve il simbolo a, si transita in uno stato (q', c) il cui primo elemento rappresenta lo stato in cui transita M 1 quando da q riceve a ed il cui secondo elemento rappresenta l'output che , nella macchina di Mealy, avrebbe assunto l'output transitando in quello stato dallo stato q a fronte di un certo input a.

Minimizzazione degli ASF • Poiché, come vedremo, un automa é un modello astratto di una macchina sequenziale, é intuitivo il fatto che sia conveniente minimizzare un automa, ovvero trovare un automa equivalente che abbia il minimo numero di stati. Ridurre il numero di stati infatti equivale a ridurre il numero di componenti di memoria nel circuito corrispondente.

Distinguibilità • Sia dato un automa di Moore M (Q, S, D, d, l, q 0). Due stati p e q si dicono distinguibili in una macchina di Moore se gli output associati a p e q sono diversi, o se per qualche sequenza di simboli a 1 a 2. . an ricevuti a partire da p e q, si transita in due stati p' e q' caratterizzati da output diversi.

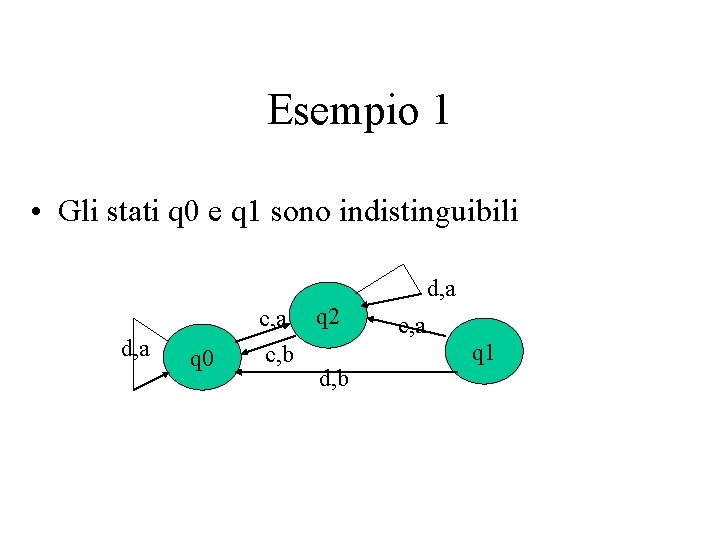
Esempio 1 • Gli stati q 0 e q 1 sono indistinguibili d, a q 0 c, a q 2 c, b d, b c, a q 1

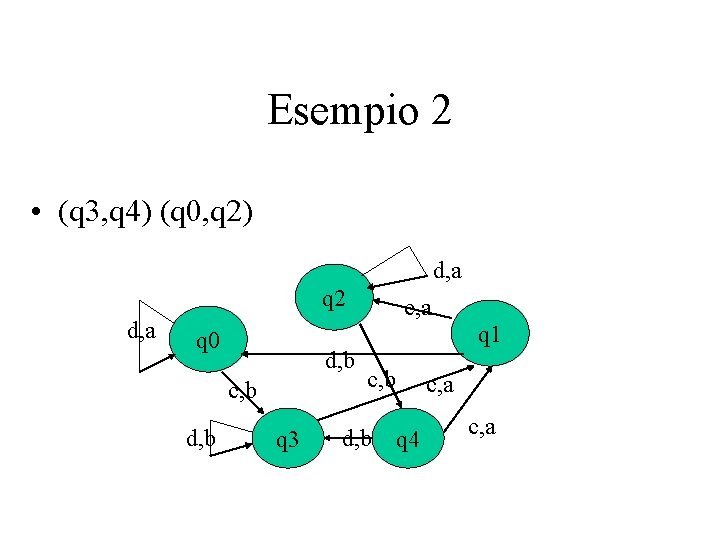
Esempio 2 • (q 3, q 4) (q 0, q 2) d, a q 2 d, a q 0 d, b c, b d, b q 3 c, a q 1 c, b d, b c, a q 4 c, a

Passo 1; tabella triangolare • Si traccia, a partire dall'automa o dalla sua tabella degli stati futuri, una tabella triangolare che permetta, ai suoi incroci, di indicare il risultato del confronto di ogni possibile coppia di stati. q 1 q 2 q 3 q 4 q 0 q 1 q 2 q 3

Passo 2: marcatura delle celle • Si esaminano una dopo l'altra tutte le possibili coppie di righe della tabella degli stati futuri, inserendo nel corrispondente incrocio della tabella triangolare: – una X se in almeno una colonna risultano specificate uscite diverse – la denominazione della coppia di stati futuri individuati colonna per colonna se in tutte le colonne le uscite risultano uguali. – non si scrive nulla nel caso in cui le indicazioni di stato futuro siano identiche o coincidano con la denominazione della coppia di stati presa in esame

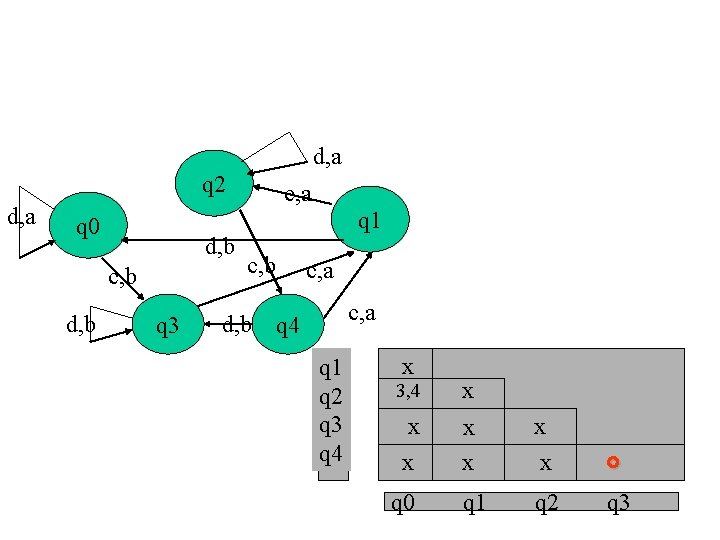
d, a q 2 d, a q 0 d, b c, b d, b q 3 c, a q 1 c, b d, b c, a q 4 q 1 q 2 q 3 q 4 x 3, 4 x x x x q 0 q 1 q 2 q 3

Osservazioni

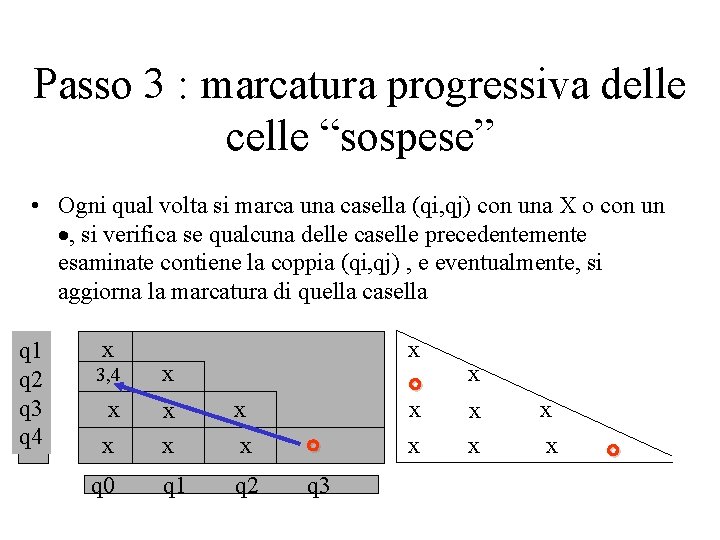
Passo 3 : marcatura progressiva delle celle “sospese” • Ogni qual volta si marca una casella (qi, qj) con una X o con un , si verifica se qualcuna delle caselle precedentemente esaminate contiene la coppia (qi, qj) , e eventualmente, si aggiorna la marcatura di quella casella q 1 q 2 q 3 q 4 x x 3, 4 x x x x q 0 q 1 q 2 q 3 x x x x

Passo 4: classi di indistinguibilità • Procedendo da destra verso sinistra si esaminano una dopo l'altra le colonne della tabella triangolare contenente caselle con il pallino e si costruisce un corrispondente sottoinsieme S con la denominazione della colonna stessa e delle righe relative • Si controllano via i sottoinsiemi che risultano contenuti in sottoinsiemi individuati. Questi sottoinsiemi prendono il nome di classi di indistinguibilità. Es: S 1: q 0, q 2 e S 2: q 3, q 4 • Si costruisce la tabella degli stati futuri minima (o il grafo) copiando solo le righe della tabella di partenza che corrispondono al primo stato di ciascuna classe di indistinguibilità, e correggendo di conseguenza le indicazioni dello stato futuro.

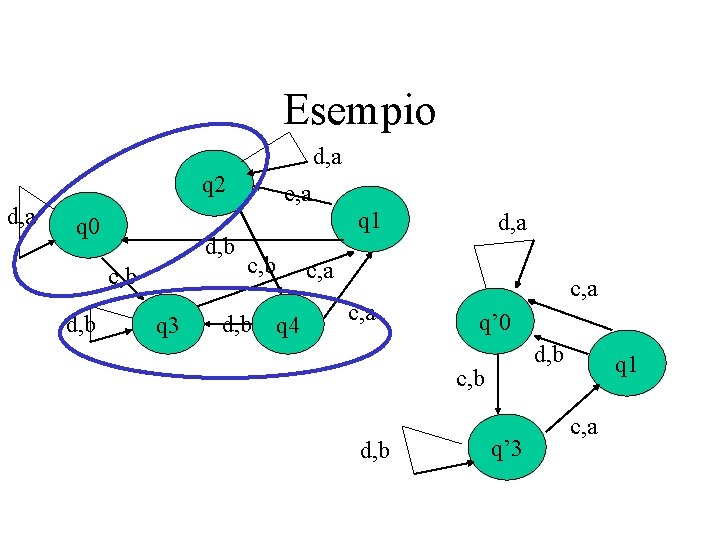
Esempio d, a q 2 d, a q 0 d, b c, b d, b q 3 c, a q 1 c, b d, a c, a q 4 c, a q’ 0 d, b c, b d, b q’ 3 q 1 c, a