Algorithmique parallle 5 Algorithmes parallles sur les matrices

Algorithmique parallèle

5. Algorithmes parallèles sur les matrices. 1. Multiplication matrice-vecteur sur un anneau. 2. Multiplication de matrices 3. Décomposition LU.

5. 1 Multiplication matrice-vecteur sur un anneau.

Produit matrice-vecteur. • Multiplication de matrice avec un vecteur: Ax=y – Avec A une matrice de dimension n*n – x un vecteur de n éléments. • Pour chaque i=1 à n faire Pour chaque j=1 à n faire y(i) =y(i) + x(i)*a(j, i)

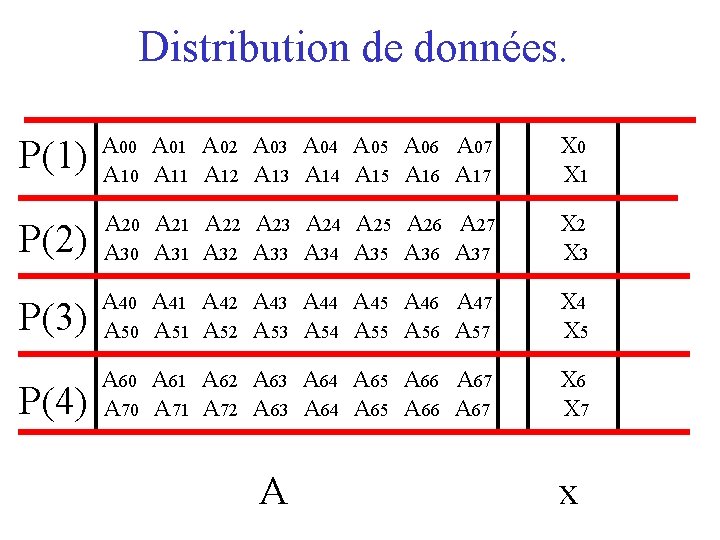
Produit matrice-vecteur. • Ax=y : Pour chaque i=1 à n faire Pour chaque j=1 à n faire y(i) =y(i) + x(i)*a(j, i) • Supposons que n/p =r. – 1 processeur contient r lignes consécutives de A. – vecteur x dupliqué sur chaque processeur.

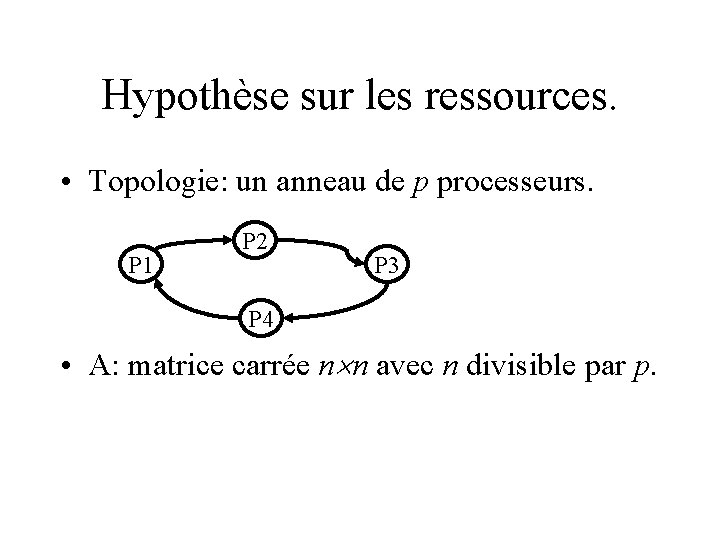
Hypothèse sur les ressources. • Topologie: un anneau de p processeurs. P 1 P 2 P 3 P 4 • A: matrice carrée n n avec n divisible par p.

Distribution de données. P(1) A 00 A 01 A 02 A 03 A 04 A 05 A 06 A 07 A 10 A 11 A 12 A 13 A 14 A 15 A 16 A 17 X 0 X 1 P(2) A 20 A 21 A 22 A 23 A 24 A 25 A 26 A 27 A 30 A 31 A 32 A 33 A 34 A 35 A 36 A 37 X 2 X 3 P(3) A 40 A 41 A 42 A 43 A 44 A 45 A 46 A 47 A 50 A 51 A 52 A 53 A 54 A 55 A 56 A 57 X 4 X 5 P(4) A 60 A 61 A 62 A 63 A 64 A 65 A 66 A 67 A 70 A 71 A 72 A 63 A 64 A 65 A 66 A 67 X 6 X 7 A x

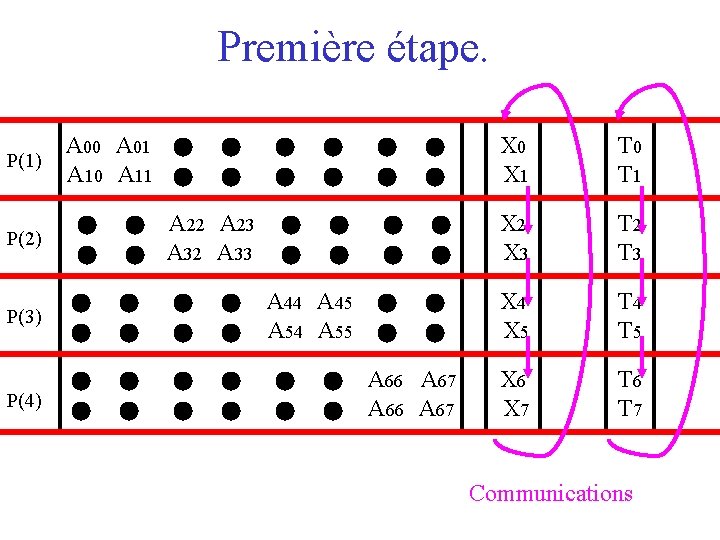
Première étape. P(1) A 00 A 01 A 02 A 03 A 04 A 05 A 06 A 07 A 10 A 11 A 12 A 13 A 14 A 15 A 16 A 17 X 0 X 1 T 0 T 1 P(2) A 20 A 21 A 22 A 23 A 24 A 25 A 26 A 27 A 30 A 31 A 32 A 33 A 34 A 35 A 36 A 37 X 2 X 3 T 2 T 3 P(3) A 40 A 41 A 42 A 43 A 44 A 45 A 46 A 47 A 50 A 51 A 52 A 53 A 54 A 55 A 56 A 57 X 4 X 5 T 4 T 5 P(4) A 60 A 61 A 62 A 63 A 64 A 65 A 66 A 67 A 70 A 71 A 72 A 63 A 64 A 65 A 66 A 67 X 6 X 7 T 6 T 7 Communications

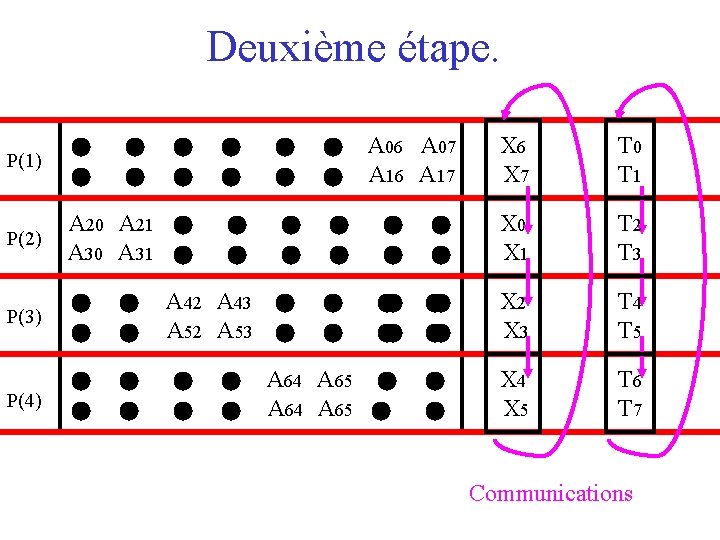
Deuxième étape. P(1) A 00 A 01 A 02 A 03 A 04 A 05 A 06 A 07 A 10 A 11 A 12 A 13 A 14 A 15 A 16 A 17 X 6 X 7 T 0 T 1 P(2) A 20 A 21 A 22 A 23 A 24 A 25 A 26 A 27 A 30 A 31 A 32 A 33 A 34 A 35 A 36 A 37 X 0 X 1 T 2 T 3 P(3) A 40 A 41 A 42 A 43 A 44 A 45 A 46 A 47 A 50 A 51 A 52 A 53 A 54 A 55 A 56 A 57 X 2 X 3 T 4 T 5 P(4) A 60 A 61 A 62 A 63 A 64 A 65 A 66 A 67 A 70 A 71 A 72 A 63 A 64 A 65 A 66 A 67 X 4 X 5 T 6 T 7 Communications

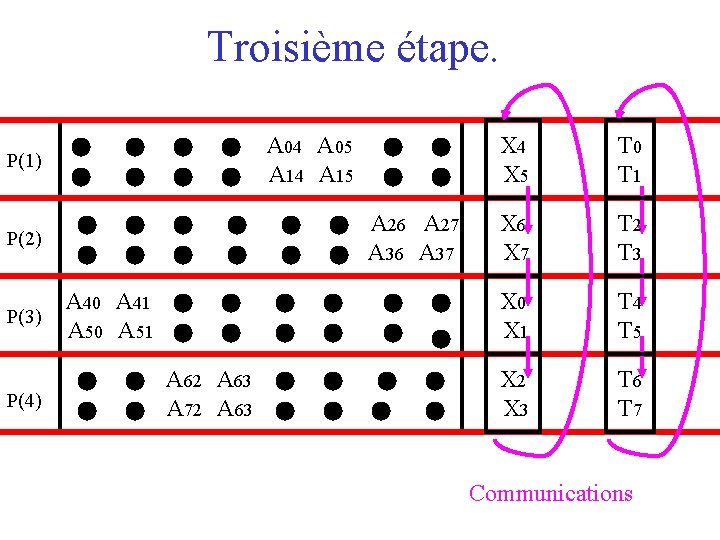
Troisième étape. P(1) A 00 A 01 A 02 A 03 A 04 A 05 A 06 A 07 A 10 A 11 A 12 A 13 A 14 A 15 A 16 A 17 X 4 X 5 T 0 T 1 P(2) A 20 A 21 A 22 A 23 A 24 A 25 A 26 A 27 A 30 A 31 A 32 A 33 A 34 A 35 A 36 A 37 X 6 X 7 T 2 T 3 P(3) A 40 A 41 A 42 A 43 A 44 A 45 A 46 A 47 A 50 A 51 A 52 A 53 A 54 A 55 A 56 A 57 X 0 X 1 T 4 T 5 P(4) A 60 A 61 A 62 A 63 A 64 A 65 A 66 A 67 A 70 A 71 A 72 A 63 A 64 A 65 A 66 A 67 X 2 X 3 T 6 T 7 Communications

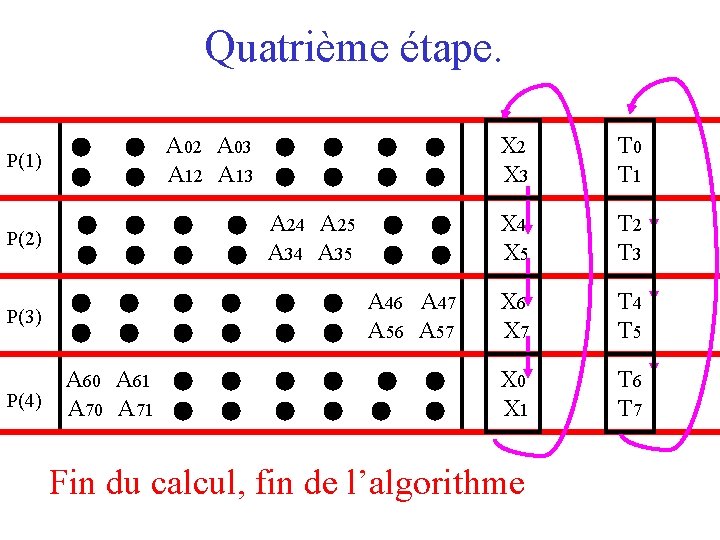
Quatrième étape. P(1) A 00 A 01 A 02 A 03 A 04 A 05 A 06 A 07 A 10 A 11 A 12 A 13 A 14 A 15 A 16 A 17 X 2 X 3 T 0 T 1 P(2) A 20 A 21 A 22 A 23 A 24 A 25 A 26 A 27 A 30 A 31 A 32 A 33 A 34 A 35 A 36 A 37 X 4 X 5 T 2 T 3 P(3) A 40 A 41 A 42 A 43 A 44 A 45 A 46 A 47 A 50 A 51 A 52 A 53 A 54 A 55 A 56 A 57 X 6 X 7 T 4 T 5 P(4) A 60 A 61 A 62 A 63 A 64 A 65 A 66 A 67 A 70 A 71 A 72 A 63 A 64 A 65 A 66 A 67 X 0 X 1 T 6 T 7 Fin du calcul, fin de l’algorithme

Résumé. • Chaque processeur possède r lignes de la matrice. • Principe de l’algorithme: faire circuler le vecteur X afin de calculer au fur et à mesure le vecteur Y. • Coût (1 seule étape) dépend d’un – coût du produit d’une matrice r*r et d’un vecteur. – une communication d’un vecteur de r éléments. • Coût total = (p-1)*coût(1 seule étape). = (p-1)max{r 2 ta, +r tc } (ta, , tc : tps d’une opération, d’init de comm, tps de comm)

5. 2 Multiplication de matrices.

Produit de matrice (1/2) • Soit A une matrice m n et B une matrice n p. n • Calculer C=A*B sachant que cij = k=1 a ik b kj • Algorithme : – Calculer aik b – Calculer c ij kj en parallèle O(1) opérations en // O(log n) opérations en //

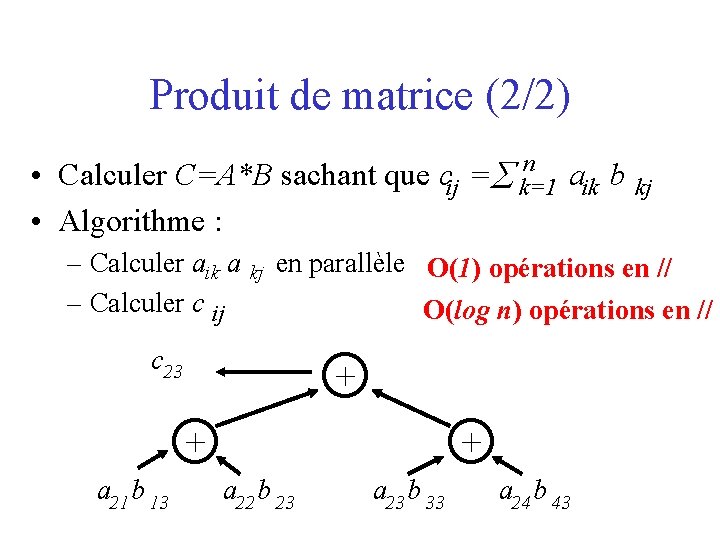
Produit de matrice (2/2) • Calculer C=A*B sachant que • Algorithme : – Calculer aik a – Calculer c ij kj n cij = k=1 en parallèle O(1) opérations en // c 23 O(log n) opérations en // + + a 21 b 13 aik b kj + a 22 b 23 a 23 b 33 a 24 b 43

Récapitulatif: produit de matrice • Soit M(n) le nombre d’opérations utilisées par le meilleur séquentiel algorithme pour multiplier 2 matrices n n. • Coût de l’algorithme parallèle dans les machines CREW PRAM – O(M(n)) en le nombre d’opérations. – O(log n) en temps.

5. 3 Décomposition LU.

Définition de la décomposition LU. • Matrice A=LU = * – Avec L une matrice triangulaire inférieure – Avec U une matrice triangulaire supérieure 2 6 4 2 0 0 1 3 2 • A = 1 1 -2 = 1 -2 0 * 0 1 2 2 5 5 2 -1 3 0 0 1

Application: décomposition LU (1/2) • Matrice A=LU = * • Résoudre d’un système linéaire : A*x =b A*x =(LU)*x =L*(U*x) =b revient à – Résoudre L* y =b – Et à résoudre U*x =y * =

Application: décomposition LU (2/2) • Matrice: A= LU = * • Autres applications: – calcul du déterminant de A. det(A)=det(L)*det(U) – Calcul de la matrice inverse A-1

Pivot de Gauss. 2 6 4 A= 1 5 -2 3 5 5 1 0 0 = ½ 1 0 * 3/2 0 1 L(0) L(1) – 1/2*L(0) L(2) – 3/2*L(0) 2 6 4 0 2 -4 0 -4 -1 2 6 4 U= 0 2 -4 0 -4 -1

Pivot de Gauss. 2 6 4 0 2 -4 = 0 -4 -1 L(0) L(1) L(2) +4/2*L(1) 1 0 0 2 6 4 0 1 0 * 0 2 -4 0 -2 1 0 0 -9 2 6 4 U= 0 2 -4 0 0 -9

2 6 4 A= 1 5 -2 3 5 5 Or 1 0 0 = ½ 1 0 * 3/2 0 1 2 6 4 0 2 -4 = 0 -4 -1 2 6 4 A= 1 5 -2 3 5 5 1 0 0 0 1 0 0 -2 1 2 6 4 0 2 -4 0 -4 -1 2 6 4 * 0 2 -4 0 0 -9 1 0 0 2 6 4 = ½ 1 0 * 0 2 -4 3/2 -2 1 0 0 -9

Algorithme séquentiel. • Soit A une matrice n n indicée 0 à n-1. Pour k=0 à n-2 faire préparation(k): Pour j=k+1 à n-1 faire a ik= -a ik /akk Pour j=k+1 à n-1 faire Pour i=k+1 à n-1 faire update(k, j): a ij = a ij +a ik *a kj

Parallélisation de l’algorithme. • Hypothèse des ressources : – A une matrice n n – Connaissance de son numéro, – Connaissance du nombre total de processeurs. – Fonction d’allocation des colonnes alloc. • Distribution des données: – 1 colonne par processeur.

Première version de la parallélisation id: =my_id(); Pour k=0 à n-2 faire si alloc(k)=id alors préparation(k): Pour j=k+1 à n-1 faire buff i-k-1= -a ik /akk diffuser(alloc(k), buff, n-k) Pour j=k+1 à n-1 faire Pour i=k+1 à n-1 faire update(k, j): a ij= a ij +buff i-k *a kj

Distribution des données : r colonnes par processeurs l: =0; Pour k=0 à n-2 faire si alloc(k)=id alors préparation(k): Pour j=k+1 à n-1 faire buffi-k-1= -a il /a kl l: =l+1; diffuser(alloc(k), buff, n-k) Pour j=l à r-1 faire Pour i=k+1 à n-1 faire update(k, j): a = a +buff *a ij ij i-k kj

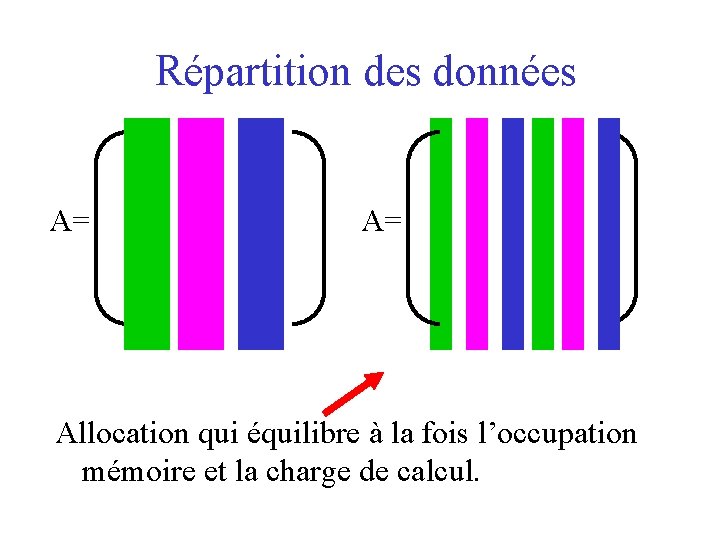
Répartition des données A= A= Allocation qui équilibre à la fois l’occupation mémoire et la charge de calcul.

Coût de l’algorithme. • colonne j est affectée au processeur j mod p j-1 # opérations sur la colonne j= (n-k-1)*ta k=0 • Temps d’exécution: – n-1 communications: n( +n/2 tc) – Préparation du pivot: n*ta*n/2 – mise à jours: ta*n 3/3 p +O(n*n) • p petit devant n, la parallélisation relativement efficace

Topologie anneau: pipeline. • Dès qu’un processeur reçoit la colonne pivot à l’étape k, – il la transmet à son successeur. – Puis il effectue ses calculs… P 1 P 2 P 4 P 3

Exemple: • Quatre processeurs • 16 colonnes, … Comment réduire les périodes d’inactivité des processeurs ?

Comment réduire les périodes d’inactivité des processeurs ? • Solution: inter-lasser les instructions. • Comment? propager le plus rapidement possible les colonnes pivots c’est-à-dire calculer dès que possible.

Plus précisement, par exemple le comportement du processeur P(1) 1. À l’étape k=0, P(1) reçoit la colonne pivot de P(0). 2. P(1) le fait passer à son voisin P(2). 3. P(1) met à jour ses colonnes j en sa possession par les instructions update(0, j). 4. P(1) passe alors à l’étape k=1 et prépare le pivot. 5. P(1) envoie la colonne pivot 1 à son voisin P(2). 6. P(1) met à jour ses colonnes j en sa possession par les instructions update(1, j).

Modification du comportement du processeur P(1) 1. À l’étape k=0, P(1) reçoit la colonne pivot de P(0). 2. P(1) le fait passer à son voisin P(2). 3. P(1) met à jour sa colonne 1 par l’instruction update(0, 1). 4. P(1) passe alors à l’étape k=1 et prépare le pivot. 5. P(1) envoie la colonne pivot 1 à son voisin P(2). 3’. P(1) met à jour ses colonnes j en sa possession par les instructions update(0, j). 6. P(1) met à jour ses colonnes j en sa possession par les instructions update(1, j).

Exemple: • Quatre processeurs • 16 colonnes, …

Autre méthode de calcul de décomposition LU A(1, 1) A(1, 2) L(1, 1) 0 U(1, 1) U(1, 2) = * A(2, 1) A(2, 2) L(1, 2) L(2, 2) 0 U(2, 2) Algorithme: diviser pour régner • A(1, 1) = L(1, 1) *U(1, 1) • A(1, 2) = L(1, 1) *U(1, 2) • A(2, 1) = L(1, 2) *U(1, 1) • A(2, 2) = L(1, 2) *U(1, 2)+ L(2, 2) *U(2, 2)

Autre méthode : décomposition LU Algorithme: diviser pour régner • • A(1, 1) = L(1, 1) *U(1, 1) A(1, 2) = L(1, 1) *U(1, 2) A(2, 1) = L(1, 2) *U(1, 1) A(2, 2) = L(1, 2) *U(1, 2)+ L(2, 2) *U(2, 2) 1. Calculer le produit A-1(1, 1)*A(1, 2), A(2, 1)* A(1, 1)-1 , A(2, 1)* A (1, 2) 2. Calculer récursivement • la décomposition A(1, 1), (c’est-à-dire L(1, 1), U(1, 1)) • -1 et de A(2, 2)- A(2, 1)* A (1, 2) (c’est-à-dire L(2, 2), U(2, 2)) -1 3. Calculer L(1, 2)= (A (2, 1)*A(1, 1))*L(1, 1) 4. Calculer U(1, 2)=U(1, 1) ( A-1(1, 1)*A(1, 2)),

Complexité: Les matrices L et U ont été calculé – en temps O(log 3 n) – en O(n. M(n)) opérations Car tps d’exécution: T(n) =T(n/2)+ O(log 2 n) # opérations: W(n) =I(n/2)+5 M(n/2) +W(n/2)+ O(n 2)