ACOUSTICS part 2 Sound Engineering Course Angelo Farina

ACOUSTICS part - 2 Sound Engineering Course Angelo Farina Dip. di Ingegneria Industriale - Università di Parma Parco Area delle Scienze 181/A, 43100 Parma – Italy angelo. farina@unipr. it www. angelofarina. it

Decibels

The Decibel scale (1): What are decibels, and why are they used? : The physical quantities related to sound amplitude have an huge dynamic range: • 1 p. W/m 2 (hearing threshold) 1 W/m 2 (pain threshold) [1012 ratio] • 20 Pa (hearing threshold) [106 ratio] 20 Pa (pain threshold) The human perception compresses such wide dynamic ranges in a much lesser variable perception. Hence a logirthmic compression is employed, for mimicing the human perception law. The advanatge of empoloying a logarithmic scale is to “linearize” the perceived loudness perception (roughly, the loudness doubles every increase of intensity of a factor of 10);

The Decibel scale (2): The sound pressure level “Lp” or SPL, is defined as: • Lp = 10 log p 2/prif 2 = 20 log p/prif (d. B) @ prif = 20 Pa The particle velocity level “Lv” is defined as: • Lv = 10 log v 2/vrif 2 = 20 log v/vrif (d. B) @ vrif = 50 nm/s. The sound intensity level “LI” is defined as: • LI = 10 log I/Irif (d. B) @ Irif = 10 -12 W/m 2. The energy density level “LD” is defined as: • LD = 10 log D/Drif (d. B) @ Drif = 3· 10 -15 J/m 3. In the simple case (plane progressive wave) ( oco = 400 rayl): • p/u= oco I = p 2/ oco =D·c 0 => hence Lp = Lv = LI = L D

The Decibel scale (3): The sound power level “LW” is defined as: • LW = 10 log W/Wrif (d. B) @ Wrif = 10 -12 W. But, while the fiorst 4 levels have all the sam emenaing (how loud a sound is perceived), and assume the very same value in the simple case of the plane, progressive wave, instead the Sound Power Level value is generally different, and possibly much larger than the first 4 values! In the simple case of plane, progressive wave (piston having area S at the entrance of a pipe), the relationship among sound power level and sound intensity level is: : • LW = LI + 10 log S/So =LI + 10 log S (d. B) If the surface area S represent the total surface over which the power flows away from the source, the above relationship is substantially always valid, even if the radiated sound field is NOT a plane progresive wave.

The human auditory system

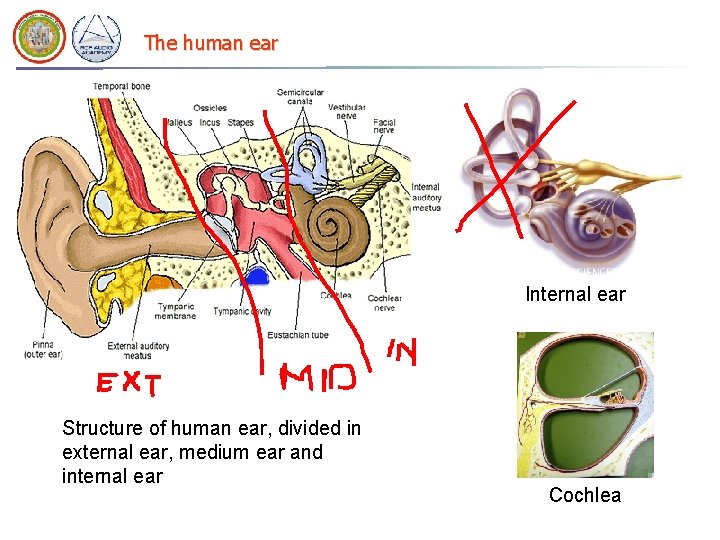
The human ear Internal ear Structure of human ear, divided in external ear, medium ear and internal ear Cochlea

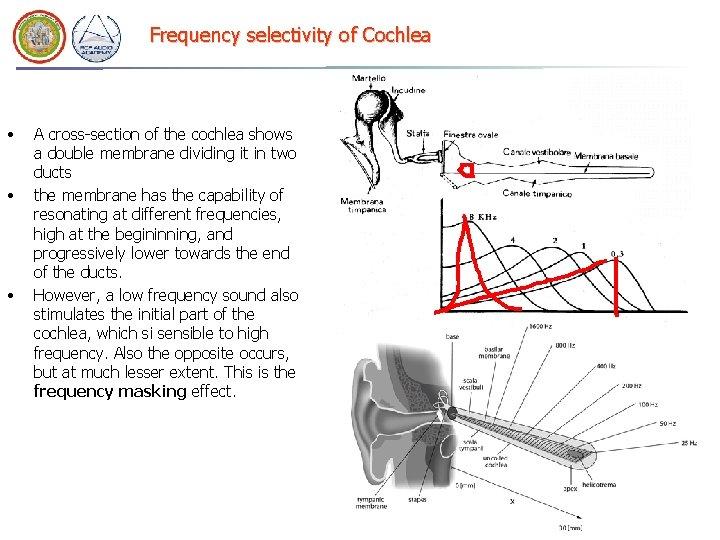
Frequency selectivity of Cochlea • • • A cross-section of the cochlea shows a double membrane dividing it in two ducts the membrane has the capability of resonating at different frequencies, high at the begininning, and progressively lower towards the end of the ducts. However, a low frequency sound also stimulates the initial part of the cochlea, which si sensible to high frequency. Also the opposite occurs, but at much lesser extent. This is the frequency masking effect.

The Cochlea • Each point of the cochlea reacts maximally to one given frequency, as shown here for the human cochlea:

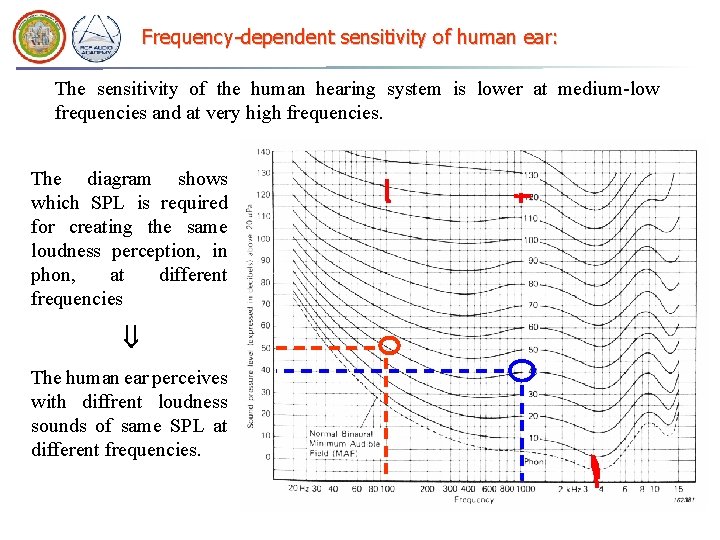
Frequency-dependent sensitivity of human ear: The sensitivity of the human hearing system is lower at medium-low frequencies and at very high frequencies. The diagram shows which SPL is required for creating the same loudness perception, in phon, at different frequencies The human ear perceives with diffrent loudness sounds of same SPL at different frequencies.

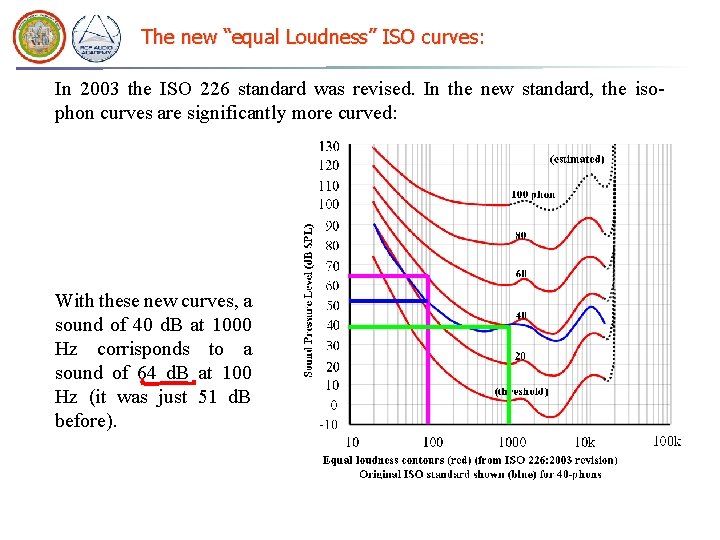
The new “equal Loudness” ISO curves: In 2003 the ISO 226 standard was revised. In the new standard, the isophon curves are significantly more curved: With these new curves, a sound of 40 d. B at 1000 Hz corrisponds to a sound of 64 d. B at 100 Hz (it was just 51 d. B before).

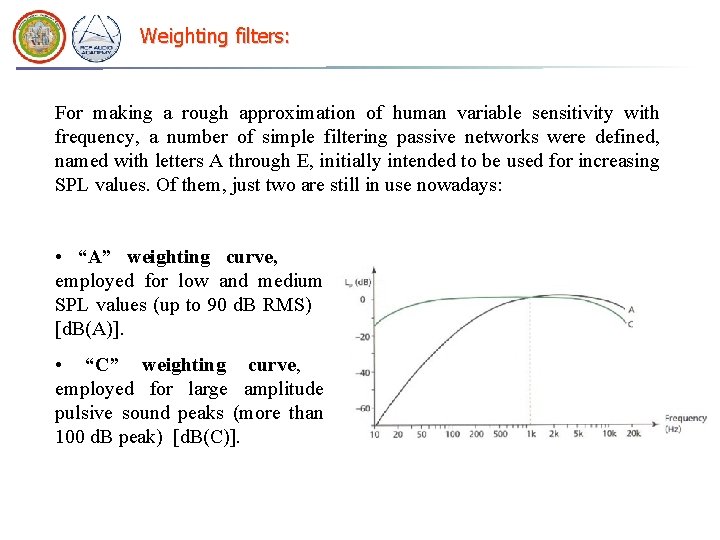
Weighting filters: For making a rough approximation of human variable sensitivity with frequency, a number of simple filtering passive networks were defined, named with letters A through E, initially intended to be used for increasing SPL values. Of them, just two are still in use nowadays: • “A” weighting curve, employed for low and medium SPL values (up to 90 d. B RMS) [d. B(A)]. • “C” weighting curve, employed for large amplitude pulsive sound peaks (more than 100 d. B peak) [d. B(C)].

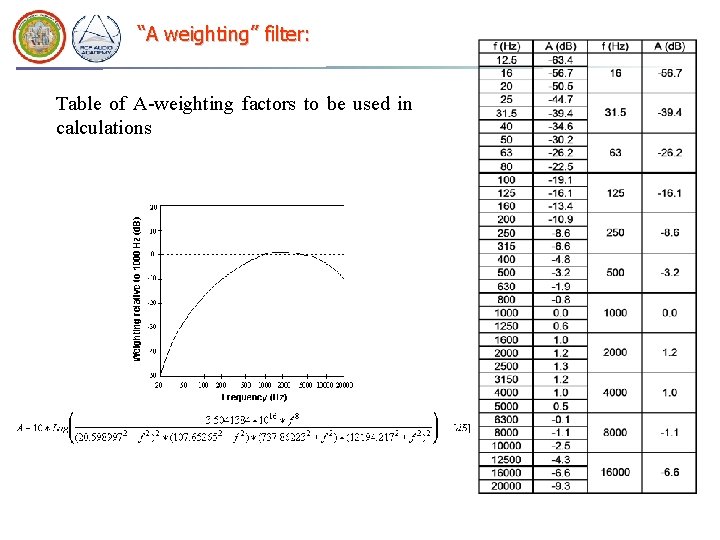
“A weighting” filter: Table of A-weighting factors to be used in calculations

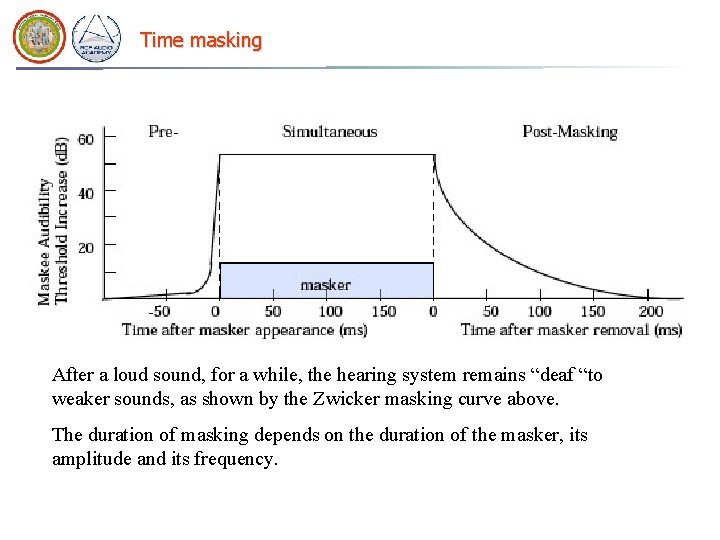
Time masking After a loud sound, for a while, the hearing system remains “deaf “to weaker sounds, as shown by the Zwicker masking curve above. The duration of masking depends on the duration of the masker, its amplitude and its frequency.

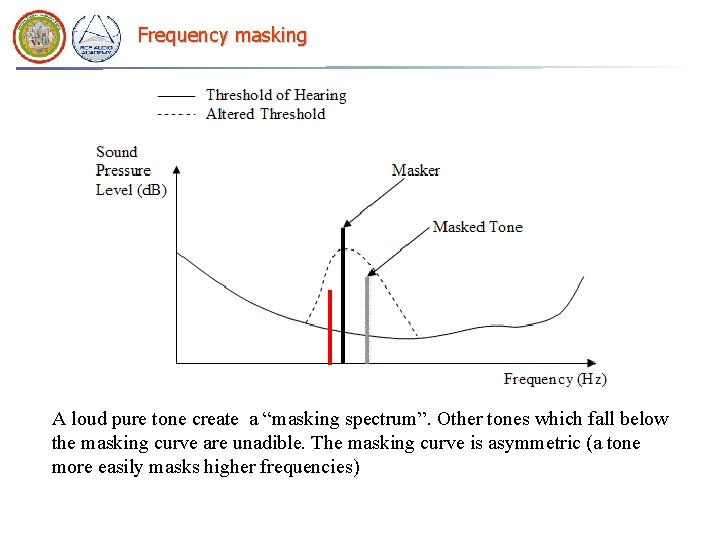
Frequency masking A loud pure tone create a “masking spectrum”. Other tones which fall below the masking curve are unadible. The masking curve is asymmetric (a tone more easily masks higher frequencies)

Sound pressure measurement: sound level meters

The sound level meter A SLM measures a value in d. B, which is the sound pressure level evaluated by the RMS value of the sound pressure, prms averaged over the measurement time T: with

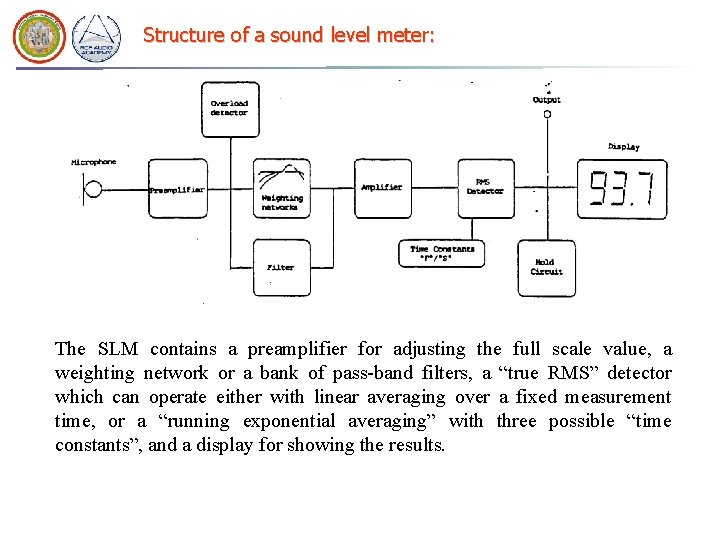
Structure of a sound level meter: The SLM contains a preamplifier for adjusting the full scale value, a weighting network or a bank of pass-band filters, a “true RMS” detector which can operate either with linear averaging over a fixed measurement time, or a “running exponential averaging” with three possible “time constants”, and a display for showing the results.

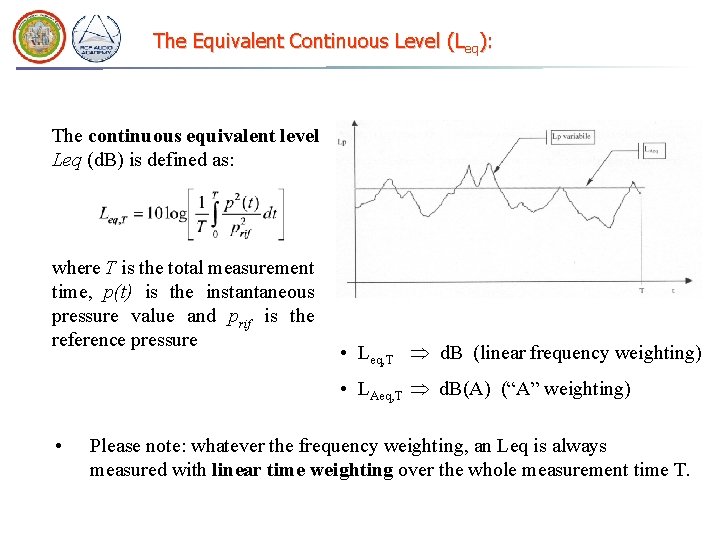
The Equivalent Continuous Level (Leq): The continuous equivalent level Leq (d. B) is defined as: where T is the total measurement time, p(t) is the instantaneous pressure value and prif is the reference pressure • Leq, T d. B (linear frequency weighting) • LAeq, T d. B(A) (“A” weighting) • Please note: whatever the frequency weighting, an Leq is always measured with linear time weighting over the whole measurement time T.

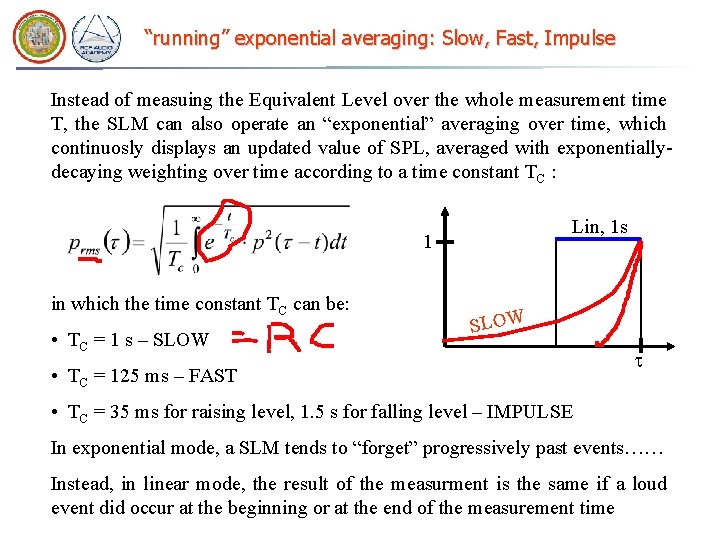
“running” exponential averaging: Slow, Fast, Impulse Instead of measuing the Equivalent Level over the whole measurement time T, the SLM can also operate an “exponential” averaging over time, which continuosly displays an updated value of SPL, averaged with exponentiallydecaying weighting over time according to a time constant TC : Lin, 1 s 1 in which the time constant TC can be: • TC = 1 s – SLOW • TC = 125 ms – FAST t • TC = 35 ms for raising level, 1. 5 s for falling level – IMPULSE In exponential mode, a SLM tends to “forget” progressively past events…… Instead, in linear mode, the result of the measurment is the same if a loud event did occur at the beginning or at the end of the measurement time

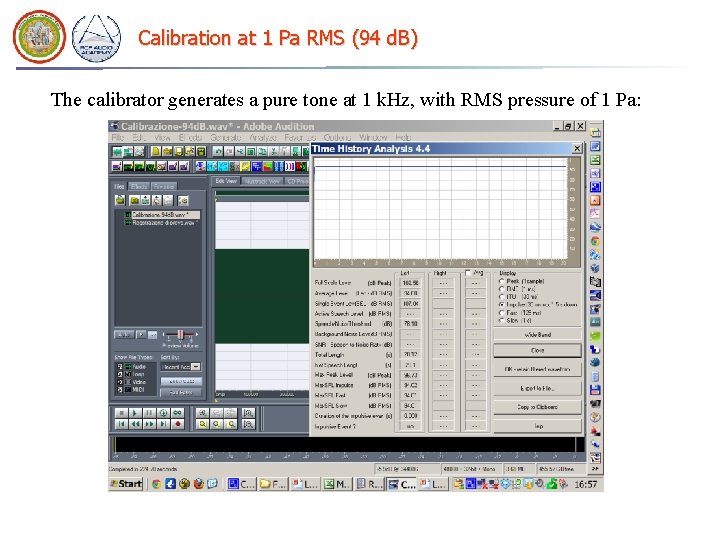
Calibration at 1 Pa RMS (94 d. B) The calibrator generates a pure tone at 1 k. Hz, with RMS pressure of 1 Pa:

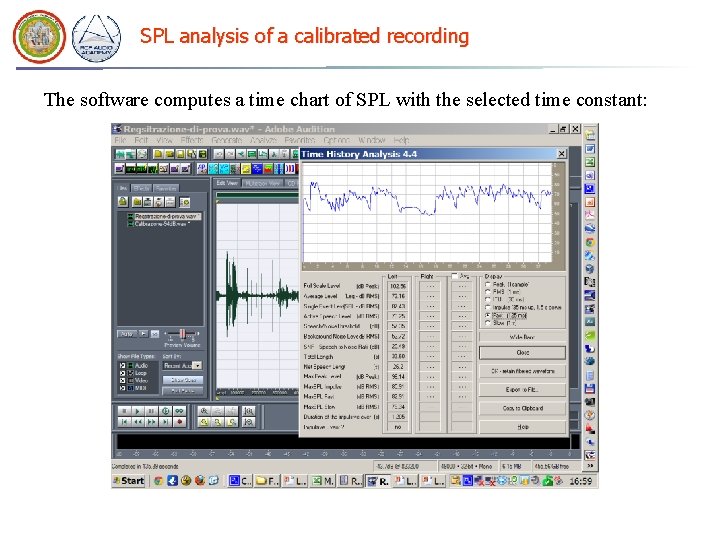
SPL analysis of a calibrated recording The software computes a time chart of SPL with the selected time constant:

Sound level summation in d. B (1): “Incoherent” sum of two “different” sounds: Lp 1 = 10 log (p 1/prif)2 = 10 Lp 1/10 Lp 2 = 10 log (p 2/prif)2 = 10 Lp 2/10 (p. T/prif)2 = (p 1/prif)2 + (p 2/prif)2 = 10 Lp 1/10 + 10 Lp 2/10 Lp. T = Lp 1 + Lp 2 = 10 log (p. T/prif)2 = 10 log (10 Lp 1/10 + 10 Lp 2/10 )

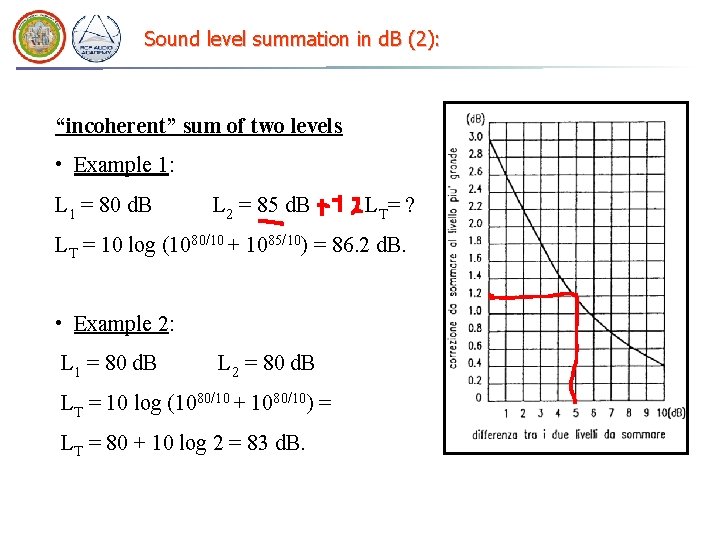
Sound level summation in d. B (2): “incoherent” sum of two levels • Example 1: L 1 = 80 d. B L 2 = 85 d. B L T= ? LT = 10 log (1080/10 + 1085/10) = 86. 2 d. B. • Example 2: L 1 = 80 d. B L 2 = 80 d. B LT = 10 log (1080/10 + 1080/10) = LT = 80 + 10 log 2 = 83 d. B.

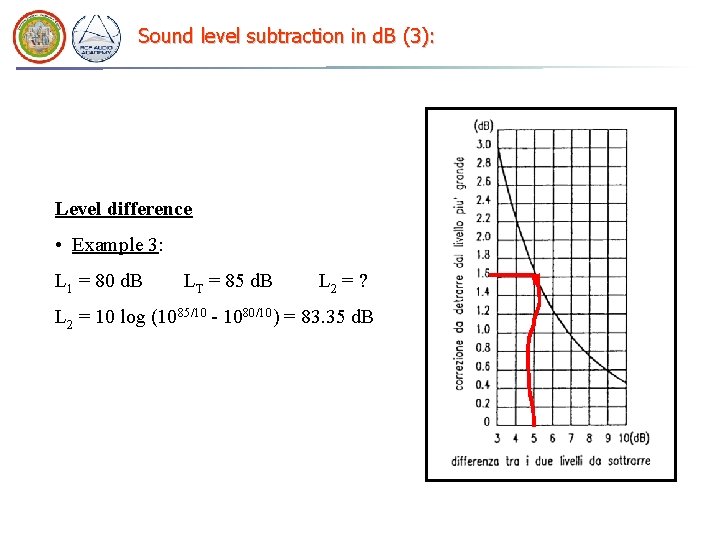
Sound level subtraction in d. B (3): Level difference • Example 3: L 1 = 80 d. B LT = 85 d. B L 2 = ? L 2 = 10 log (1085/10 - 1080/10) = 83. 35 d. B

Sound level summation in d. B (4): “Coherent” sum of two (identical) sounds: Lp 1 = 20 log (p 1/prif) = 10 Lp 1/20 Lp 2 = 20 log (p 2/prif) = 10 Lp 2/20 (p. T/prif) = (p 1/prif)+ (p 2/prif) = 10 Lp 1/20 + 10 Lp 2/20 Lp. T = Lp 1 + Lp 2 = 10 log (p. T/prif)2 = 20 log (10 Lp 1/20 + 10 Lp 2/20 )

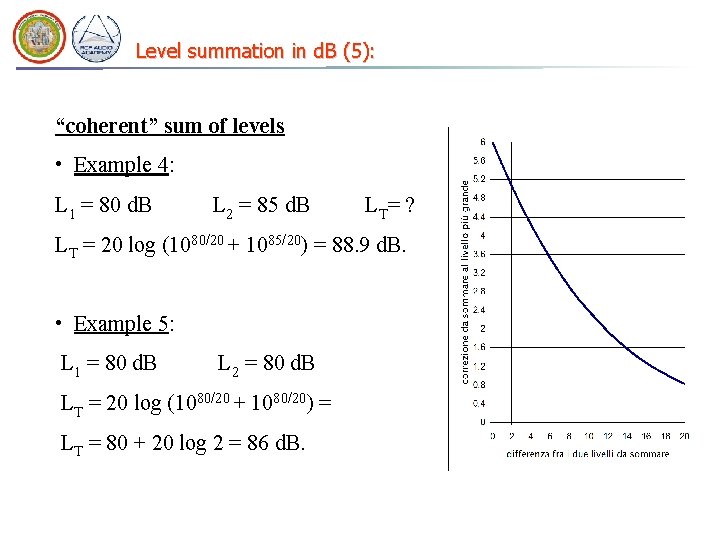
Level summation in d. B (5): “coherent” sum of levels • Example 4: L 1 = 80 d. B L 2 = 85 d. B L T= ? LT = 20 log (1080/20 + 1085/20) = 88. 9 d. B. • Example 5: L 1 = 80 d. B L 2 = 80 d. B LT = 20 log (1080/20 + 1080/20) = LT = 80 + 20 log 2 = 86 d. B.