A New Transitive Closure Algorithm with Application to

A New Transitive Closure Algorithm with Application to Redundancy Identification Vivek Gaur Avant! Corp. , Fremont, CA 94538, USA vgaur@avanticorp. com Vishwani D. Agrawal Agere Systems, Murray Hill, NJ 07974, USA va@agere. com http: //cm. bell-labs. com/cm/cs/who/va Michael L. Bushnell Rutgers University, Dept. of ECE, Piscataway, NJ 08854, USA bushnell@caip. rutgers. edu Jan. 29, 2002 Gaur, et al. : DELTA'02 1

Talk Outline • Problem Statement • Background – Redundancy Identification • Implication graph • Partial implications • Transitive closure • Redundancy identification • Results • Conclusion Jan. 29, 2002 Gaur, et al. : DELTA'02 2

Problem Statement • Many problems can be solved by implication graphs and transitive closure. • We will study the problem of redundancy identification. • Redundancy identification has applications in testing and in circuit optimization. Jan. 29, 2002 Gaur, et al. : DELTA'02 3

Redundancy Identification • ATPG based method • Exhaustive test pattern generation to find • whether or not a target fault has a test. All redundant faults can be found, but ATPG cost is exponential in circuit size. • Fault independent method • Method analyzes circuit topology and • • • function locally; no specific fault targeted. Many (not all) redundant faults can be found at a lower cost. FIRE, Iyer and Abramovici, VLSI Design’ 94. TC, Agrawal, Bushnell and Qing, ATS’ 96. Jan. 29, 2002 Gaur, et al. : DELTA'02 4

Use of Implication Graphs • Implication graphs: • Chakradhar, et al. , Book’ 90 • Larrabee, IEEE-TCAD’ 92 • Transitive closure: • ATPG: Chakradhar, et al. , IEEE-TCAD’ 93 • Redundancy, Agrawal, et al. , ATS’ 96 • Partial implications: • Henftling, et al. , EDAC’ 95 • Gaur, MS Thesis’ 02, Rutgers University Jan. 29, 2002 Gaur, et al. : DELTA'02 5

Implication graph An implication graph is a representation of logical implications between pairs of signals of a digital circuit. • Nodes • Two nodes per signal; nodes a and a correspond to signal a. • A node has two states (true, false); represents the signal state. • Edges • A directed edge from node a to b means “a=1” implies “b=1”. Jan. 29, 2002 Gaur, et al. : DELTA'02 6

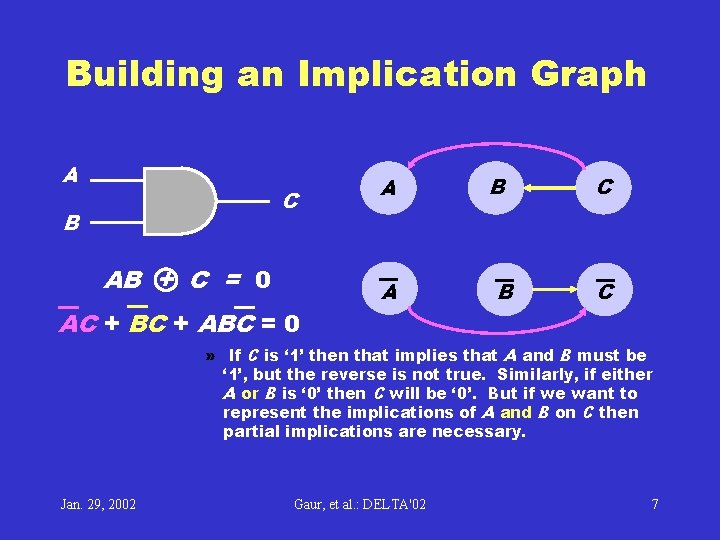
Building an Implication Graph A C B AB + C = 0 AC + BC + ABC = 0 A A B B C C » If C is ‘ 1’ then that implies that A and B must be ‘ 1’, but the reverse is not true. Similarly, if either A or B is ‘ 0’ then C will be ‘ 0’. But if we want to represent the implications of A and B on C then partial implications are necessary. Jan. 29, 2002 Gaur, et al. : DELTA'02 7

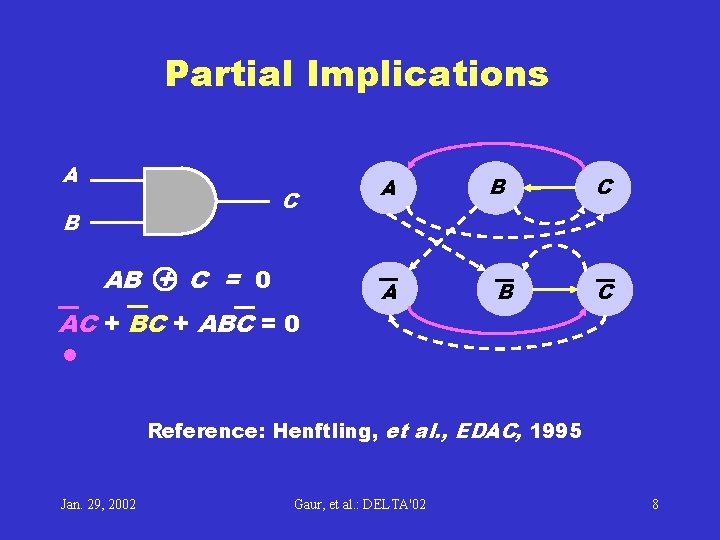
Partial Implications A C B AB + C = 0 AC + BC + ABC = 0 A A B B C C • Reference: Henftling, et al. , EDAC, 1995 Jan. 29, 2002 Gaur, et al. : DELTA'02 8

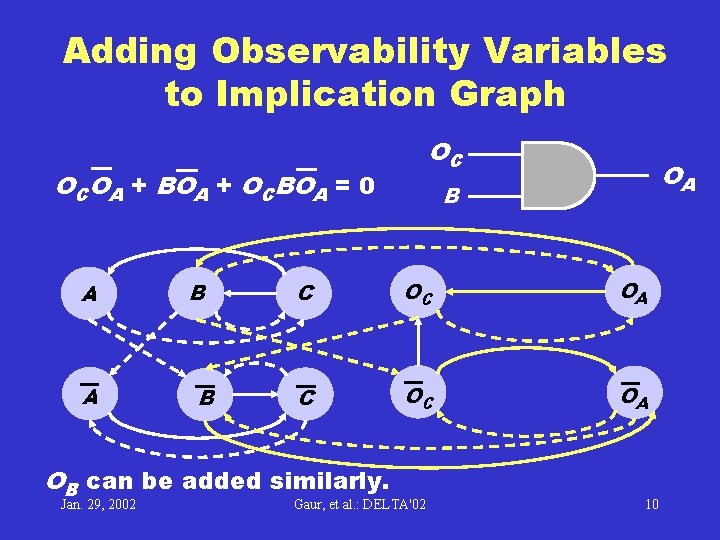
Observability Variables Observability variable of a signal represents whether or not that signal is observable at a PO. It can be true or false. A B OA OB OC = 1 C (PO) OC B OA OC B + O A = 0 OCOA + BOA + OCBOA = 0 Jan. 29, 2002 Gaur, et al. : DELTA'02 9

Adding Observability Variables to Implication Graph OC OCOA + BOA + OCBOA = 0 A A B B B C OC OA OB can be added similarly. Jan. 29, 2002 OA Gaur, et al. : DELTA'02 10

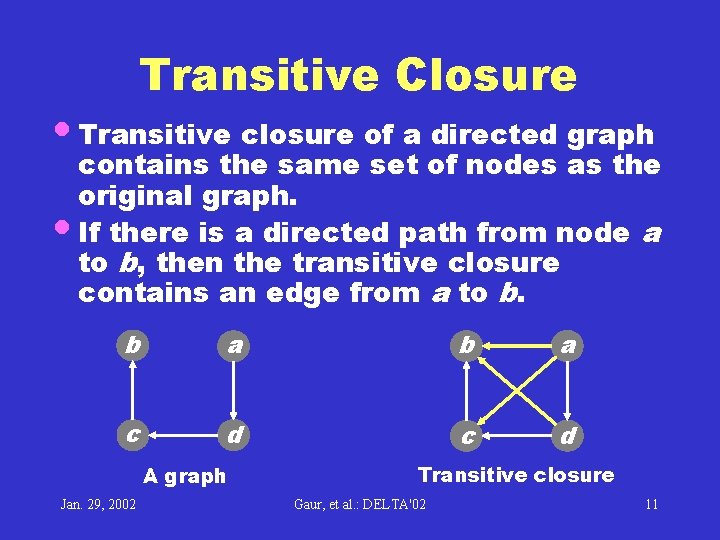
Transitive Closure • Transitive closure of a directed graph contains the same set of nodes as the original graph. • If there is a directed path from node a to b, then the transitive closure contains an edge from a to b. b a c d A graph Jan. 29, 2002 Transitive closure Gaur, et al. : DELTA'02 11

Stuck-at Fault Redundancy • Detection of a fault requires the fault to be activated and its effect observed at a PO. • Example: Fault a s-a-1 is detectable, iff following conditions can be simultaneously satisfied: • a=0 • Oa = 1 Jan. 29, 2002 Gaur, et al. : DELTA'02 12

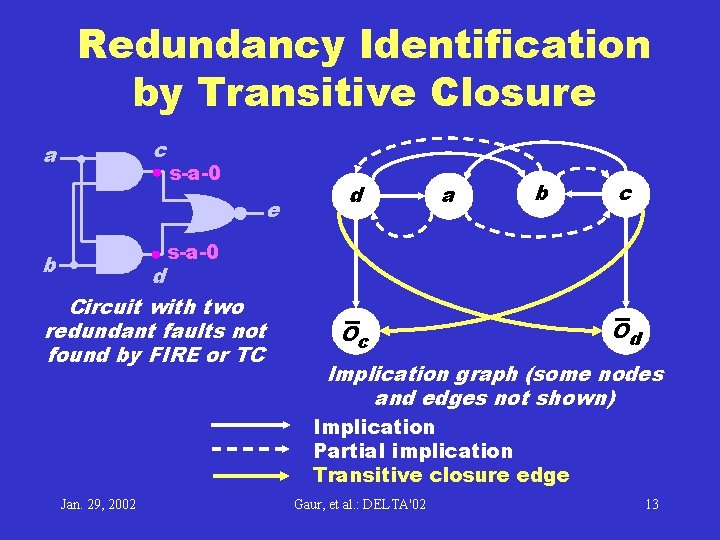
Redundancy Identification by Transitive Closure c a s-a-0 e d a b c s-a-0 b d Circuit with two redundant faults not found by FIRE or TC Oc Od Implication graph (some nodes and edges not shown) Implication Partial implication Transitive closure edge Jan. 29, 2002 Gaur, et al. : DELTA'02 13

• • Method Summarized Obtain an implication graph from the circuit topology and compute transitive closure: • • Path-tracing algorithm (see this paper). Matrix method (see, Gaur, MS Thesis, Rutgers U. , 2002). Examine all nodes: • S-a-0 is redundant if the signal implies its complement. • S-a-1 is redundant if the complement of the signal implies the signal. • Both faults are redundant if the signal and its complement imply each other. • S-a-0 is redundant if the signal implies its false observability variable. • S-a-1 is redundant if the complement of the signal implies its false observability variable. • S-a-0 is redundant if the observability variable implies the complement of the signal. • S-a-1 is redundant if the observability variable implies the signal. • Both faults are redundant if the observability variable and its complement imply each other. Jan. 29, 2002 Gaur, et al. : DELTA'02 14

Classification of Redundant Faults by TCAND Tot. red. faults ident. 2 Unexcitable red. faults 0 Unpropagatable red. faults Undrivable red. faults C 1908 Total red. +aborted faults* 6+3 0 2 C 2670 99+18 23+2 3 3 17+2 C 3540 99+40 74 0 8 66 C 5315 59 32 1 1 30 C 6288 33 31 15 16 0 C 7552 67+76 34 3 0 31 Circuit *HITEC, Nierman and Patel, EDAC’ 91 Jan. 29, 2002 Gaur, et al. : DELTA'02 15

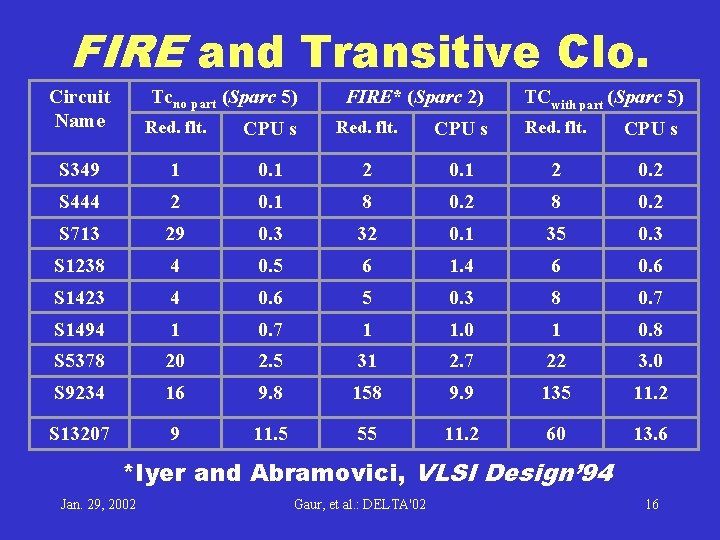
FIRE and Transitive Clo. Tcno part (Sparc 5) FIRE* (Sparc 2) TCwith part (Sparc 5) Circuit Name Red. flt. CPU s S 349 1 0. 1 2 0. 2 S 444 2 0. 1 8 0. 2 S 713 29 0. 3 32 0. 1 35 0. 3 S 1238 4 0. 5 6 1. 4 6 0. 6 S 1423 4 0. 6 5 0. 3 8 0. 7 S 1494 1 0. 7 1 1. 0 1 0. 8 S 5378 20 2. 5 31 2. 7 22 3. 0 S 9234 16 9. 8 158 9. 9 135 11. 2 S 13207 9 11. 5 55 11. 2 60 13. 6 *Iyer and Abramovici, VLSI Design’ 94 Jan. 29, 2002 Gaur, et al. : DELTA'02 16

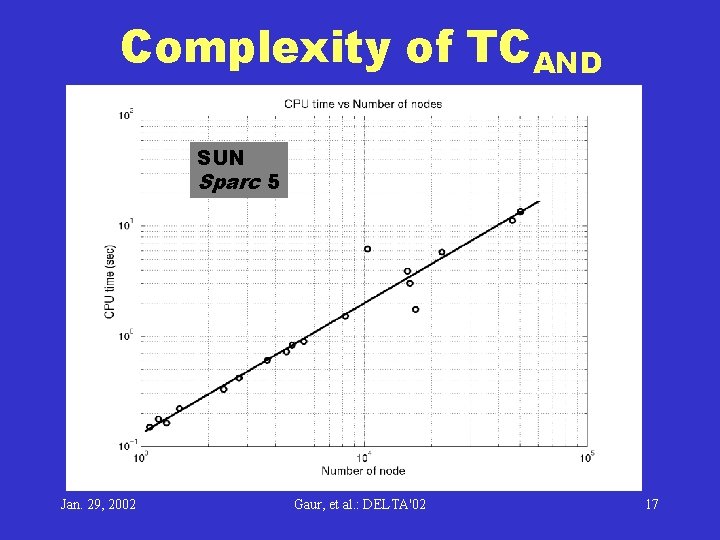
Complexity of TCAND SUN Sparc 5 Jan. 29, 2002 Gaur, et al. : DELTA'02 17

Limitation of Method • Observability variable of a fanout stem is not analyzed. • Only the redundant faults due to false controllability of fanout stem can be identified. s-a-1 s-a-0 Two redundant stem faults not identified by transitive closure Jan. 29, 2002 Three redundant s-a-0 faults identified by transitive closure Gaur, et al. : DELTA'02 18

Conclusion • Partial implications improve redundancy • • identification. Present limitation of the method is the identification of redundancy due to the false observability of fanout stem; open problem. Transitive closure computation run times were linear in the number of nodes for the implication graphs of benchmark circuits, although the known worst-case complexity is O(N 3) for N nodes. Jan. 29, 2002 Gaur, et al. : DELTA'02 19