Transitive closures again Theorem The transitive closure of
















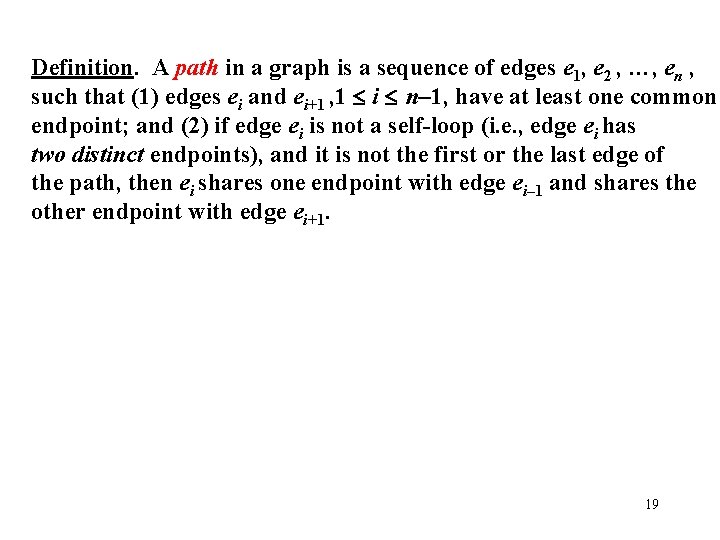




- Slides: 25

Transitive closures again. Theorem. The transitive closure of R is Proof. Denote. We need to prove that S satisfies the definition of transitive closure, i. e. i) S includes R, R S ii) S is transitive iii) S is the smallest relation satisfying i) and ii) assume (x, y) S and (y, z ) S to prove that (x, z) S. (x, y) S implies that (x, y) Rn , n is some integer, n Z+. (y, z ) S implies that (y, z ) Rm, m is some integer , n Z+. (x, z) Rno Rm= Rn+m, by the previous Theorem. (x, z) S , since Rn+m S 1

iii) Suppose T is any relation, satisfying i) R T and ii) T is transitive. and prove that S T. By the definition of S as , it suffices to prove that for any n Z+ (Rn T) We are going to prove it by induction on n 1. 1) Basis: when n=1, R 1=R T by assumption. 2) IH: Assume that for n=k, where k is some integer, k 1, Rk T. IS: Need to prove Rk+1 T Suppose (x, y) Rk+1=Rko R (by definition of composition). It implies that there exists some z A, that (x, z) Rk and (z, y) R. . (x, z) Rk implies (x, z) T , because Rk T by IH. (z, y) R implies (z, y) T , because R T by assumption. (x, z) T and (z, y) T imply (x, y) T by transitive property of T. We proved by induction that for any n 1, Rn T. 2

• Sometimes we need stronger assumption to prove IS. • It happens when to prove IS for (n +1) you need to refer not only to the previous n , but to smaller numbers. Strong Induction Principle: Let A N denote a subset that satisfies the following two properties: 1) 0 A; 2) if 0, 1, …k A, then k+1 A. Then A=N. So, Strong Induction differs from Induction Principle in step 2): IP 2) n 0 [P (n) P (n+1)] Strong Induction 2) n 0 [( m n P (m)) P (n+1)] 3

Example. Prove that every amount of postage of 12 cents or more can be formed using only 4 cent and 5 cent stamps. We are going to prove by induction on n 12, that any postage n = 5 i + 4 j, where integers i, j 0. As we proceed n n +1, we can not derive case n +1 from the case n (n+1) 5 (n+1) 4 n n +1 We can infer n+1 = 5 i + 4 j either from (n+1) 5 = 5(i 1) + 4 j or from (n+1) 4 = 5 i + 4(j 1) We need to prove an extended basis here, that is to prove the basis on more then one point. 4

Proof. 1) Basis (extended): check that we can form postage of 12, 13, 14, and 15 cents using only 4 c and 5 c stamps. 12=4 3; 13=5+ 4 2; 14=5 2+4; 15=5 3. 2) IH: Assume that any postage 12, … k, where k 15 can be made using 4 c and 5 c stamps (strong induction) IS Prove that conjecture is true for the postage k +1. By IH any postage greater or equal then 12 c and less or equal k can be formed using 4 c and 5 c stamps. In particular it is true for k 3. Together with one more 4 c stamp it gives k +1 postage. 5

Theorem. The following three principles are equivalent: (a) the Induction Principle; (b) the Strong Induction Principle; and (c) the Well-Ordering principle. Proof. It suffices to prove (a) (b), (b) (c), and (c) (a). We already did this 6

Proof of (a) (b): Let A N and A satisfies the two properties: (1) 0 A; and (2) if 0, 1, …k A then k+1 A. We need to prove A=N. To make use of Induction Principle we define the auxiliary set C={m| m N and 0, 1, …m A}. Thus, C A N (3). Since 0 A by (1), 0 C by the definition of C. If k C, that is, 0, 1, …k A, then by the property (2) of the set A, k+1 A, which implies that k+1 C, because 0, 1, …k, k+1 A. Thus, set C satisfies the properties of the Induction Principle, so C=N. Therefore A=N because of (3). 7

Proof of (b) (c): Assume B N and B (4). Suppose the Well-Ordering Principle is false, i. e. suppose B does not have the smallest element (5). Prove that this leads to contradiction to the Strong Induction Principle. Let A=N B (6). By (5) 0 B, thus 0 A by (6). If the numbers 0, 1, …k A, then these numbers do not belong to B. Then k+1 does not belong to B, because otherwise it would be the smallest element of B contradicting to (5). Thus, k+1 A and by the Strong Induction Principle A=N, which implies that B = by (6), contradicting to (4). So, (c) is proved. 8

Example. Prove that n Fn+1 0 1 2 3 4 5 6 7 1 1 2 3 5 8 13 21 for all n 5. 1 1. 5 2. 25 3. 375 5. 0625 7. 59375 11. 390625 17. 0859375 Basis 9

Proof by induction on n 5 that Fn+1>(3/2)n 1) Basis (extended) n=5: F 6 = 8 > (3/2)5 = 7. 59375 n=6: F 7 = 13 >(3/2)6 = 11. 390625 2) IH : Assume that for all n=5, …k, where k is some integer k 6 we have Fn+1>(3/2)n (strong induction). IS : We need to prove inequality Fn+1>(3/2)n for n = k +1, i. e. Fk+2>(3/2)k+1 Fk+2= Fk+1+ Fk ……recursive definition > (3/2)k + (3/2)k 1 ……. IH for n=k and n=k 1 = (3/2)k 1 ((3/2)+1)……algebra = (3/2)k 1 (5/2) = (3/2)k 1 (10/4) > (3/2)k 1 (9/4) = (3/2)k 1 (3/2)2 = (3/2)k+1 10

Example. Suppose the function f is defined recursively for all positive integers n by f (1)=1, f (2)=5, and for n 2 f (n+1) = f (n) + 2 f (n 1). Prove that f (n)=2 n +( 1)n 11

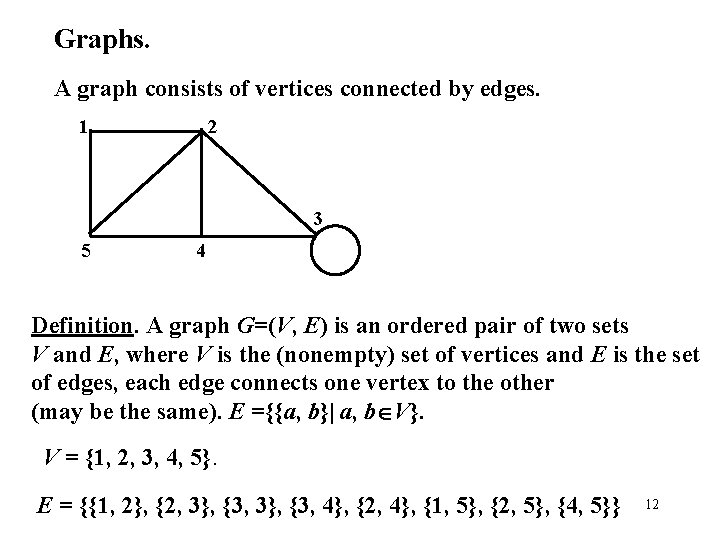
Graphs. A graph consists of vertices connected by edges. 1 2 3 5 4 Definition. A graph G=(V, E) is an ordered pair of two sets V and E, where V is the (nonempty) set of vertices and E is the set of edges, each edge connects one vertex to the other (may be the same). E ={{a, b}| a, b V}. V = {1, 2, 3, 4, 5}. E = {{1, 2}, {2, 3}, {3, 4}, {2, 4}, {1, 5}, {2, 5}, {4, 5}} 12

Sometimes, the edges of a graph have direction or orientation. Such directed edges are shown as arrows and the graph is then called a directed graph, or, a digraph. For directed graphs edges are ordered pairs, E ={(a, b)| a, b V}. Examples 1) The results of a tournament of 6 teams can be represented as a digraph: vertices are teams and arrows represent the outcomes of the games. 1 is a a winner. 1 2 6 3 5 4 13

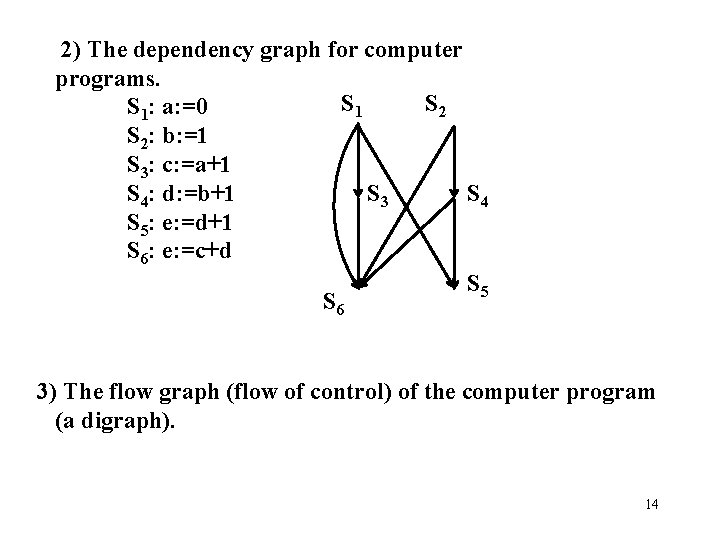
2) The dependency graph for computer programs. S 1 S 2 S 1: a: =0 S 2: b: =1 S 3: c: =a+1 S 3 S 4: d: =b+1 S 5: e: =d+1 S 6: e: =c+d S 5 S 6 3) The flow graph (flow of control) of the computer program (a digraph). 14

Definition. Two vertices u and v in an undirected graph G=(V, E) are called adjacent if e={u, v} E Edge e is called incident with the vertices u and v, or u and v are endpoints of e. Definition. The number of times a vertex u is used as an endpoint of an edge is called the degree of u, deg(u). A self-loop contributes twice to the degree of the vertex. A vertex of degree 0 is called isolated. An isolated vertex is not adjacent to any vertex. 15

Theorem. (Hand-Shaking Lemma) Let G = (V, E) denote a finite graph, that is, both |V| and |E| < . Then where the summation ranges over all vertices in V. Proof: Consider an arbitrary vertex vi of V, let deg(vi ) = n. Thus, there are edges e 1, e 2, …, en , which have one endpoint incident with vertex vi. (If there is a self-loop ej incident with vertex vi , edge ej is listed twice because both of its endpoints equal vi. ) Thus, the value of deg(vi ) counts all edges that are incident with vi. Since each edge in E connects one vertex vi to another vertex vk, the sum counts each edge exactly twice. Therefore, 16

Example. A group of people at a party shook hands with one another. We could use a graph to record all handshaking activities, where the individual persons are the vertices, and each handshaking action gives an edge between the participating individuals. The Hand-Shaking Lemma given above says, in words, the total number of hand-shaking counts from all the individuals, is equal to two times the number of hand-shaking activities. Corollary. Let G = (V, E) denote a finite graph. Then there is an even number of vertices of odd degree. Proof: Since the sum is an even number, being equal to 2 |E|, and that the summation is a sum of all even degrees and all odd degrees, the sum of only the odd degrees must be even, because the difference of two even numbers is even. Thus, there must be an even number of odd degrees, because otherwise, a sum of odd number of odd degrees is still odd. 17

Similar to the case of graphs, we can define the following terms in digraphs. The in-degree of vertex counts the number of edges pointing to the vertex (with the arrowhead at the vertex), the out-degree of a vertex counts the number of edges with the arrow-tail at the vertex. In general, (undirected) graphs can be considered as a special case of digraphs (by replacing each undirected edge with two directed edges with opposite directions). The following Hand-Shaking lemma for digraphs can be proved similarly. Theorem. Let G = (V, E) denote a finite digraph. Then 18
Definition. A path in a graph is a sequence of edges e 1, e 2 , …, en , such that (1) edges ei and ei+1 , 1 i n– 1, have at least one common endpoint; and (2) if edge ei is not a self-loop (i. e. , edge ei has two distinct endpoints), and it is not the first or the last edge of the path, then ei shares one endpoint with edge ei– 1 and shares the other endpoint with edge ei+1. 19

Definition. A path is called a cycle (or circuit) if the start vertex of the path coincides with the end vertex of the path. If no vertices appear more than once on a path, it is called a simple path; similarly, a simple cycle has no vertices appearing more than once, except for the start and the end vertices (which are identical). A graph is connected if for every pair of vertices there exists a path connecting one vertex to the other. The study of graph theory was started by mathematician Euler who in 1736 proved a famous result that relates the vertex degrees to the ability of traversing through all the edges in a single path. The town of Königsberg had 7 bridges crossing the river of Pregel, and Euler showed that it was impossible to cross each of the bridges exactly once during a walk through the town. 20

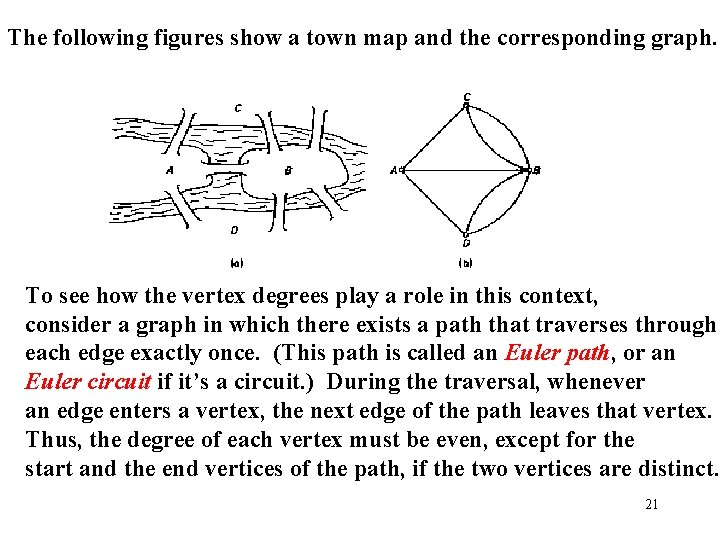
The following figures show a town map and the corresponding graph. To see how the vertex degrees play a role in this context, consider a graph in which there exists a path that traverses through each edge exactly once. (This path is called an Euler path, or an Euler circuit if it’s a circuit. ) During the traversal, whenever an edge enters a vertex, the next edge of the path leaves that vertex. Thus, the degree of each vertex must be even, except for the start and the end vertices of the path, if the two vertices are distinct. 21

Theorem. (Euler, 1736) A finite, connected graph has an Euler path iff either all vertex degrees are even (in which case there exists an Euler circuit), or exactly two vertices have odd degrees (which correspond to the start and the end vertices of an Euler path). Example. Which of the following graphs have an Euler circuit? Of those that do not, which have an Euler path? 22

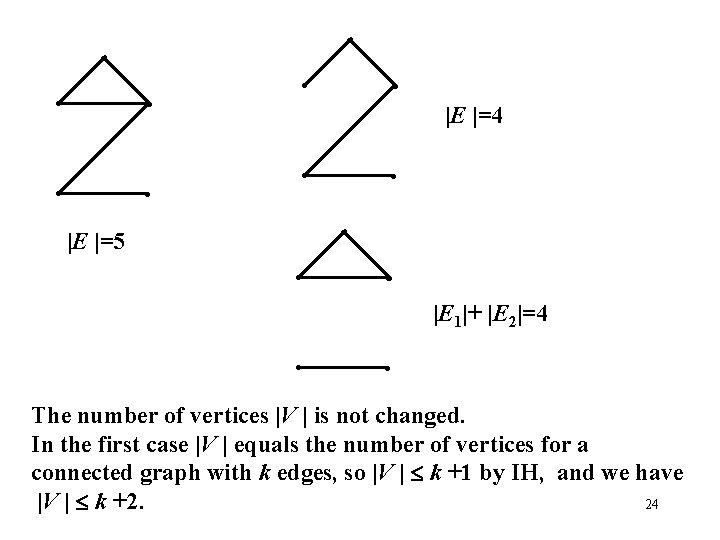
Theorem. Let G = (V, E) be nonempty connected graph. Then |E| |V | 1. Proof. We can proof that the inequality holds for connected graphs with any number of edges |E |. Proof by induction on n = |E | 0 that for any connected graph with n edges |V | n + 1. Basis. n = |E |=0. We want to show that |V | 1. But the only nonempty connected graph with |E |=0 has one vertex. IS Assume that |V | |E | + 1 for any graph with the number of edges |E | k, where k is some integer, k 0 (Strong induction). Consider any graph with | E |=k +1. We want to show that |V | |E | + 1 = k +2. If we remove one edge it might result either to one connected graph with k edges or two connected graphs 23 with |E 1|+ |E 2|=k.

• • |E |=4 • • • |E |=5 • • |E 1|+ |E 2|=4 • • The number of vertices |V | is not changed. In the first case |V | equals the number of vertices for a connected graph with k edges, so |V | k +1 by IH, and we have 24 |V | k +2.

In the second case | V | = |V 1|+|V 2| , but |V 1| |E 1| +1 and |V 2| |E 2| +1 by IH, so | V | = |V 1|+|V 2| |E 1| +1+ |E 2| +1 = k + 2. Alternative proof. We can prove that the inequality holds for connected graphs with any number of vertices |V |. Proof by induction on n = |V | 1 that for any connected graph with n vertices |E | n 1. Another problem for you to solve: If G=(V, E) is an undirected graph with |V|=v, |E|=e, and no loops, prove that 2 e v 2 v. 25