A derivlt alkalmazsa A fggvny monotonitsa A fggvny

A derivált alkalmazása A függvény monotonitása

A függvény monotonitása - a függvény szigorúan monoton növekvő - az érintő iránytényezője mindenütt pozitív - A függvény deriváltja mindenütt pozitív - a függvény szigorúan monoton csökkenő - az érintő iránytényezője mindenütt negatív - A függvény deriváltja mindenütt negatív Tóth István – Műszaki Iskola Ada

A monotonitás tétele Ha az (a, b) intervallumban differenciálható f(x) függvény az intervallumban monoton nő monoton csökken, akkor a derivált az intervallum minden pontjában nemnegatív Tóth István – Műszaki Iskola Ada nempozitív

A monotonitás Ha f ‘(x) az (a, b) intervallumban nemnegatív (nempozitív), akkor az f(x) függvény monoton növekvő (monoton csökkenő). Ha f ‘(x) az (a, b) intervallumban pozitív (negatív), akkor az f(x) függvény szigorúan monoton növekvő (szigorúan monoton csökkenő). f(x) monoton nő f(x) szigorúan monoton nő f(x) monoton csökken f(x) szigorúan monoton csökken Tóth István – Műszaki Iskola Ada

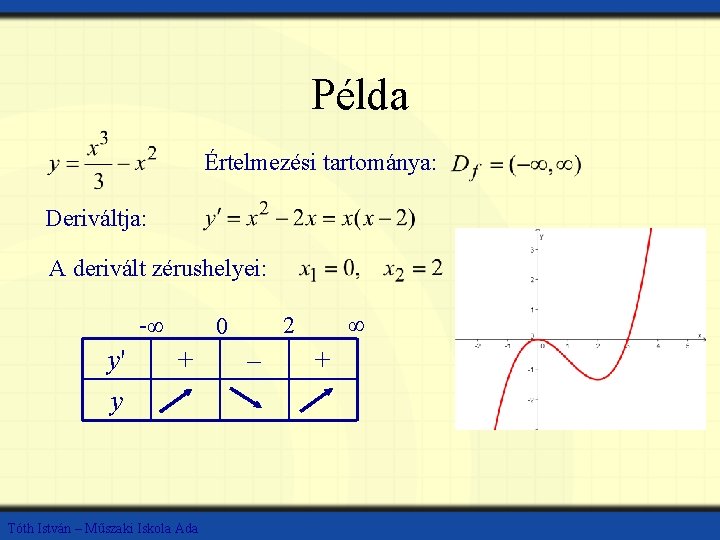
Példa Értelmezési tartománya: Deriváltja: A derivált zérushelyei: -∞ y' y + Tóth István – Műszaki Iskola Ada ∞ 2 0 – +

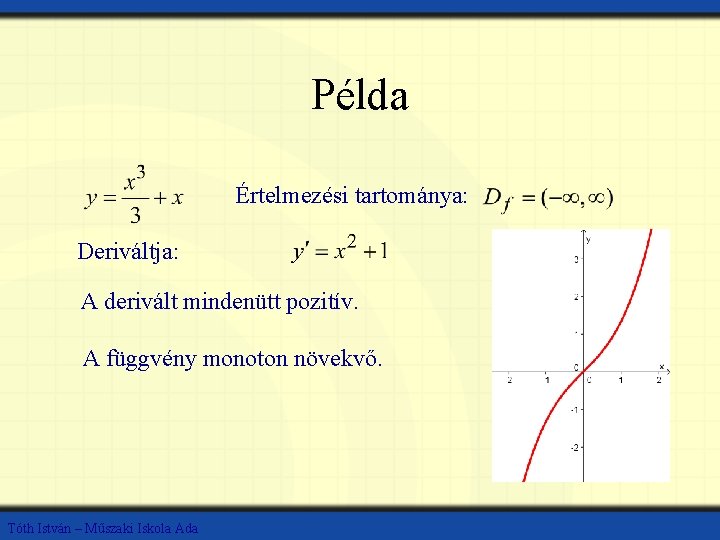
Példa Értelmezési tartománya: Deriváltja: A derivált mindenütt pozitív. A függvény monoton növekvő. Tóth István – Műszaki Iskola Ada

Példa Értelmezési tartománya: Deriváltja: A szakadási pont is kritikus pont A derivált zérushelyei: -∞ y' y 3 2 + Tóth István – Műszaki Iskola Ada – 4 – ∞ +

A derivált alkalmazása A függvény szélsőértéke

A függvény szélsőértéke Egy differenciálható f(x) függvény lokális szélsőérték helyén a görbéhez tartozó érintő párhuzamos az x tengellyel az érintő iránytényezője nulla Megfordítva nem mindig teljesül, a derivált zérushelyén a függvénynek nincs mindig szélsőértéke Tóth István – Műszaki Iskola Ada

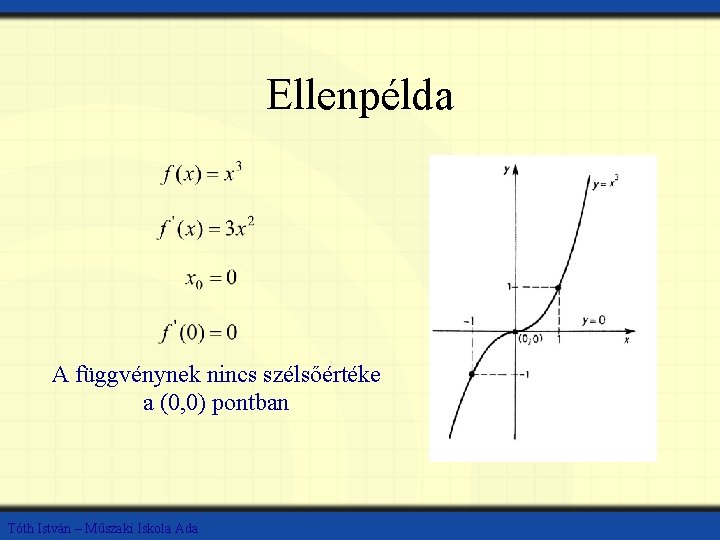
Ellenpélda A függvénynek nincs szélsőértéke a (0, 0) pontban Tóth István – Műszaki Iskola Ada

Példa Keressük meg a függvény szélsőértékeit: Értelmezési tartomány: Derivált: A derivált zérushelyei: Monotonitás: Tóth István – Műszaki Iskola Ada x -∞ ¼ y' 0 y csökk. , ha x= ¼ + növ. 1 0 0 ∞ + növ.

Példa Keressük meg a függvény szélsőértékeit: Értelmezési tartomány: Derivált: A derivált értelmezési tartománya: Monotonitás: x -∞ y' y csökk. , ha x=0 Tóth István – Műszaki Iskola Ada 0 × 0 ∞ + növ.

Feladatok Tóth István – Műszaki Iskola Ada min: max: min: max:

A derivált alkalmazása A függvény legkisebb és legnagyobb értéke zárt intervallumban

Legkisebb és legnagyobb érték [a, b] zárt intervallum: • vannak lokális szélsőértékek • a legnagyobb érték f(b) • a legkisebb érték a lokális minimum Az [a, b] zárt intervallumon folytonos f függvény legkisebb és legnagyobb értékét a lokális szélsőértékek és az intervallum végpontjai között keressük. Tóth István – Műszaki Iskola Ada

Példa Keressük meg a függvény legkisebb és legnagyobb értékét a [-1, 1] intervallumon: A derivált: Kritikus pontok: Legkisebb Legnagyobb Tóth István – Műszaki Iskola Ada

Feladatok Tóth István – Műszaki Iskola Ada min: max:

Példa 18 cm • Egy 20 cm szélességű és 18 cm magasságú, téglalap alakú kartonból hogyan tudunk maximális térfogatú, fedőlap nélküli dobozt készíteni? x x 20 cm 20 -2 x 18 -2 x x A karton sarkaiból 3, 15 cm-es oldalú négyzeteket kell levágni, az így kapott doboz térfogata 504, 91 cm 3 lesz. Tóth István – Műszaki Iskola Ada

Feladat • Az r=4 cm sugarú félkörbe maximális területű téglalapot szeretnénk írni. Határozd meg a téglalap méreteit! x Tóth István – Műszaki Iskola Ada

Feladat Tóth István – Műszaki Iskola Ada Transzformátor 200 m • A hőerőmű és a transzformátorállomás között szeretnének távvezetéket lefektetni. A két objektum egy 200 m szélességű folyó két oldalán helyezkedik el, a folyó hosszán mért 3 km távolságra egymástól. Ismeretes. hogy a folyó felett átívelő vezeték építési ára méterenként 4 ezer dinár, a szárazföldön pedig méterenként 2 ezer dinár. Az erőműből kiindulva a folyón át hol érjen túlsó partot a távvezeték, hogy építési költsége minimális legyen? Erőmű 3000 m

Megoldás Transzformátor x 0, 2 km A vezeték hossza: Építési költség (millió din. ): Erőmű d 1 d 2 3 km Minimális építési költség 6, 693 millió din, ha x=116 m. Tóth István – Műszaki Iskola Ada

A derivált alkalmazása A függvény konvexitása

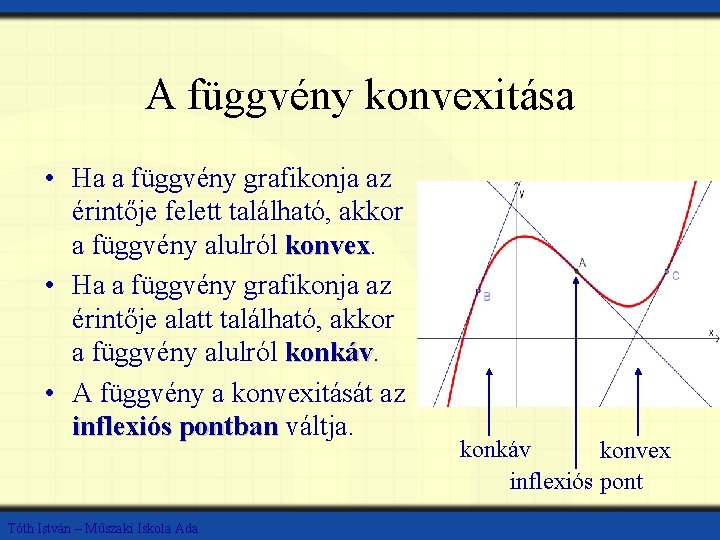
A függvény konvexitása • Ha a függvény grafikonja az érintője felett található, akkor a függvény alulról konvex • Ha a függvény grafikonja az érintője alatt található, akkor a függvény alulról konkáv • A függvény a konvexitását az inflexiós pontban váltja. Tóth István – Műszaki Iskola Ada konkáv konvex inflexiós pont

A függvény konvexitása • Ha az f(x) függvény az (a, b) intervallumban kétszer differenciálható, és f”(x)>0, akkor az f(x) függvény konvex, ha f”(x)< 0, akkor az f(x) függvény konkáv. • Ha f”(x 0)=0, és az x 0 pontban a második derivált előjelet vált, akkor az x 0 pontban a függvénynek inflexiós pontja van. Tóth István – Műszaki Iskola Ada

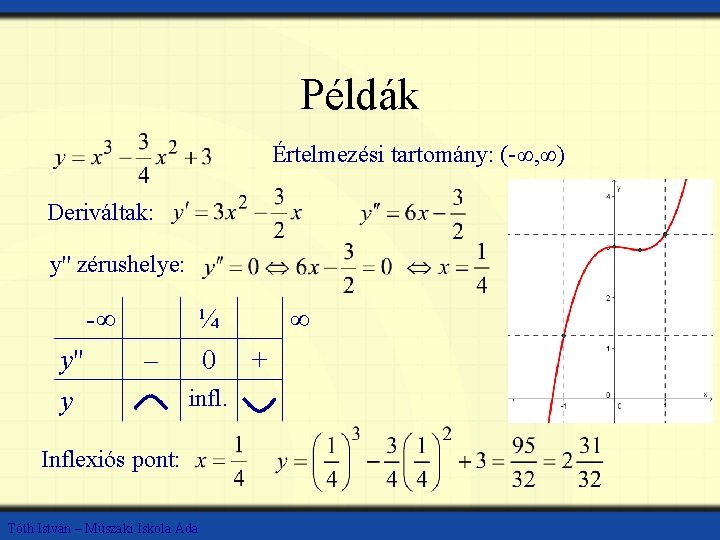
Példák Értelmezési tartomány: (-∞, ∞) Deriváltak: y'' zérushelye: -∞ y'' y – ¼ 0 infl. Inflexiós pont: Tóth István – Műszaki Iskola Ada ∞ +

Feladatok Tóth István – Műszaki Iskola Ada

A derivált alkalmazása A függvény menetének vizsgálata

A függvényvizsgálat lépései 1. 2. 3. 4. 5. 6. 7. Az értelmezési tartomány meghatározása Párosság, periodikusság stb. Zérushelyek, előjelvizsgálat Monotonitás és szélsőérték Konvexitás és inflexiós pontok Aszimptoták A grafikon felrajzolása Tóth István – Műszaki Iskola Ada

Példa Értelmezési tartomány: Párosság: Páratlan Zérushely, előjel: 0 -∞ y Tóth István – Műszaki Iskola Ada - + ∞ - +

Példa Monotonitás és szélsőérték: -1 -∞ y' y Tóth István – Műszaki Iskola Ada + növ. 1 + csökk. növ. max. min. ∞

Példa Konvexitás és inflexiós pont: -∞ y" y 0 ∞ + konkáv konvex infl. Aszimptoták: Nincs sem függőleges, sem vízszintes, sem ferde Tóth István – Műszaki Iskola Ada

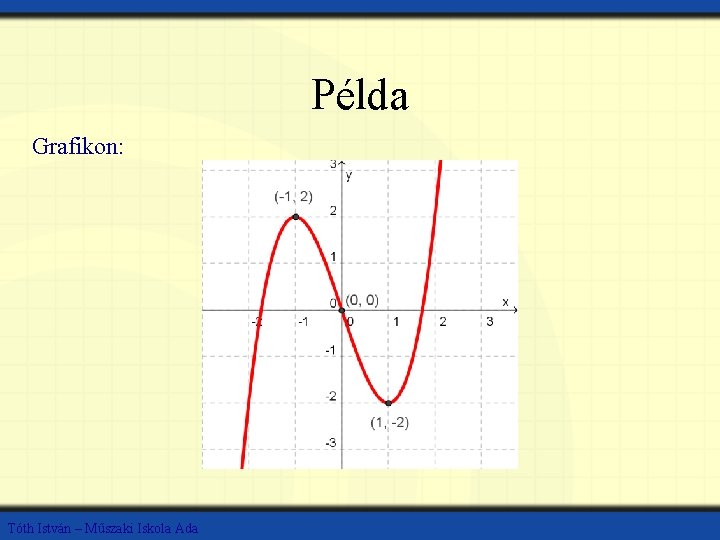
Példa Grafikon: Tóth István – Műszaki Iskola Ada

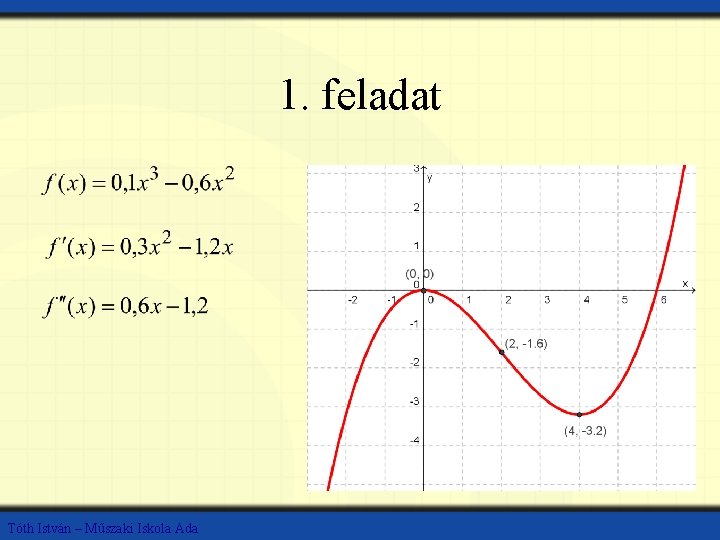
1. feladat Tóth István – Műszaki Iskola Ada

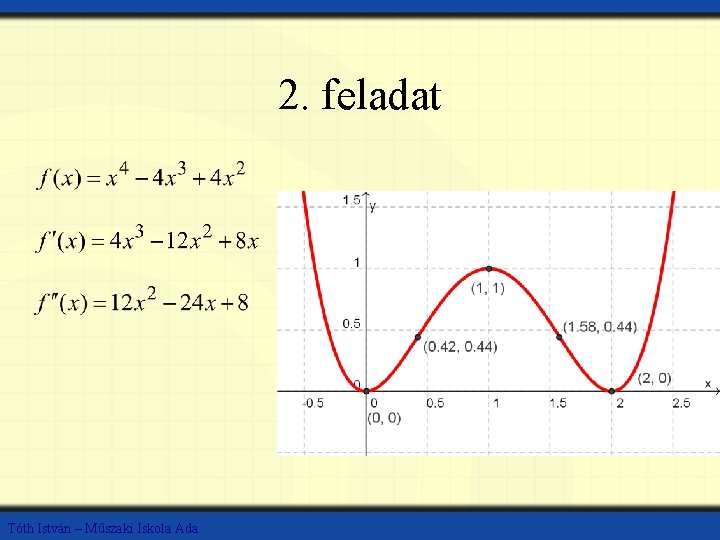
2. feladat Tóth István – Műszaki Iskola Ada

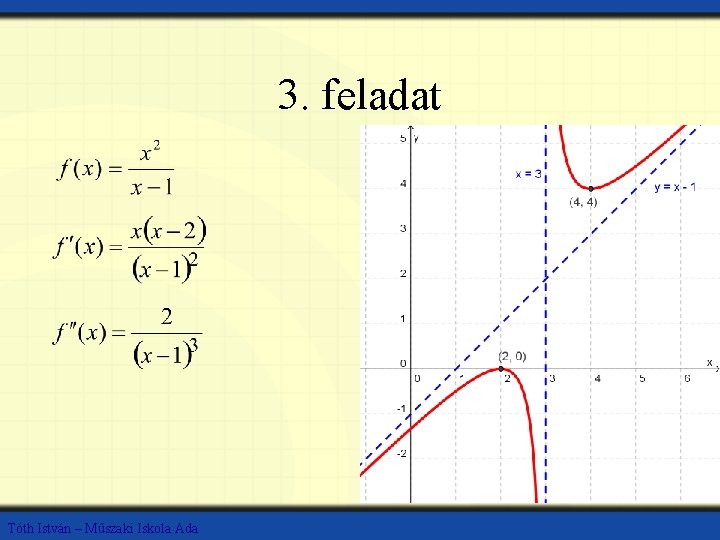
3. feladat Tóth István – Műszaki Iskola Ada

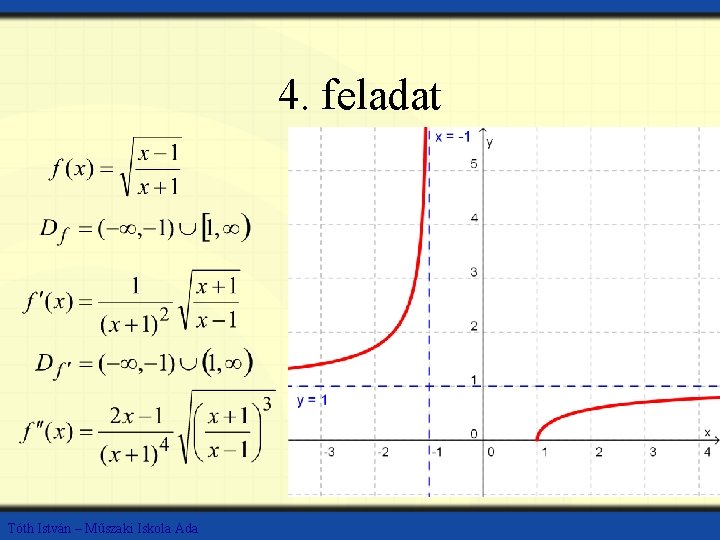
4. feladat Tóth István – Műszaki Iskola Ada

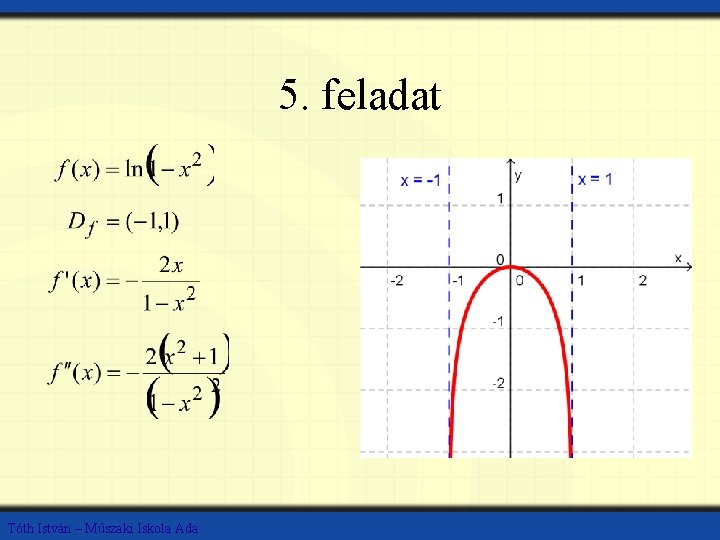
5. feladat Tóth István – Műszaki Iskola Ada

Következik: dolgozat! Tóth István – Műszaki Iskola Ada