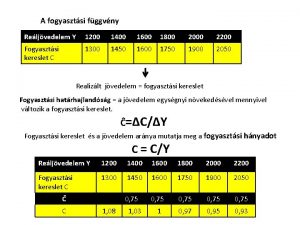
Hatrozatlan integrl Antiderivls A primitv fggvny Ha fxhez

Határozatlan integrál Antideriválás

A primitív függvény • Ha f(x)-hez létezik F(x) függvény úgy, hogy F(x) differenciálható egy [a, b] intervallumon és F '(x) = f(x) x [a, b] akkor F(x) az f(x) primitív függvénye • A primitív függvény keresése a deriválás műveletének ellentett művelete (antiderivált) Tóth István – Műszaki Iskola Ada 2

Példák Keressük azt a függvényt, amelynek deriváltja 13. mert Tóth István – Műszaki Iskola Ada 3

A primitív függvény tulajdonságai • Ha F(x) primitív függvénye f(x)-nek, akkor minden C valós számra az F(x)+C is primitív függvény. primitív, ha , tehát Tóth István – Műszaki Iskola Ada is primitív. 4

A primitív függvény tulajdonságai • Ha F(x) és G(x) primitív függvényei az f(x)-nek, akkor csak állandóban térnek el egymástól. G(x) = F(x) + C • Egy függvénynek végtelen sok primitív függvénye van. Tóth István – Műszaki Iskola Ada 5

A határozatlan integrál • Egy f(x) függvény összes primitív függvényeinek halmazát a függvény határozatlan integráljának nevezzük. Rövidebben: Tóth István – Műszaki Iskola Ada 6

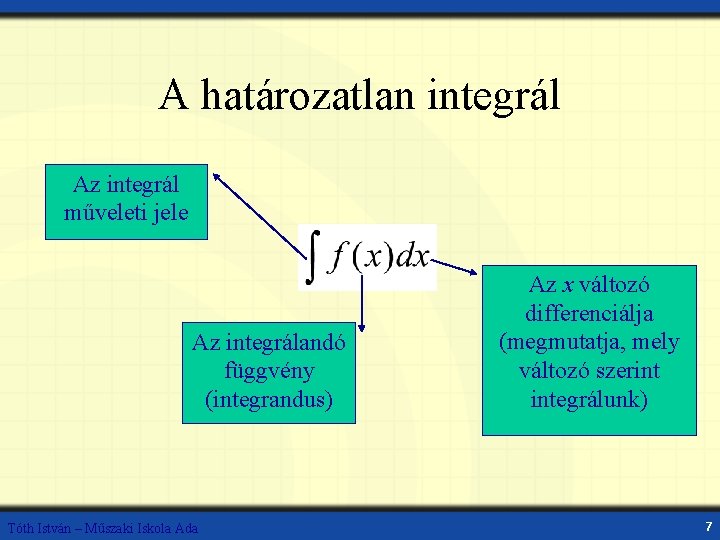
A határozatlan integrál Az integrál műveleti jele Az integrálandó függvény (integrandus) Tóth István – Műszaki Iskola Ada Az x változó differenciálja (megmutatja, mely változó szerint integrálunk) 7

A határozatlan integrál kiszámítása • alapintegrálok táblázata • integrálási szabályok • integrálási módszerek – helyettesítés módszere – parciális integrálás Tóth István – Műszaki Iskola Ada 8

Integrálok táblázata Tóth István – Műszaki Iskola Ada 9

Példák Tóth István – Műszaki Iskola Ada 10

Integrálási szabályok • Ha f(x)-nek létezik primitív függvénye és c tetszőleges valós szám, akkor • Ha f(x), g(x)-nek létezik primitív függvénye, akkor Tóth István – Műszaki Iskola Ada 11

Integrálási szabályok Szorzatra, hányadosra, összetett függvényre NINCS általános integrálási szabály !!!! Tóth István – Műszaki Iskola Ada 12

Példák Tóth István – Műszaki Iskola Ada 13

Példák Tóth István – Műszaki Iskola Ada 14

Példák Tóth István – Műszaki Iskola Ada 15

Integrálás helyettesítéssel Tóth István – Műszaki Iskola Ada 16

Példák Tóth István – Műszaki Iskola Ada 17

Példák Tóth István – Műszaki Iskola Ada 18

Példák Tóth István – Műszaki Iskola Ada 19

Tóth István – Műszaki Iskola Ada 20

Tóth István – Műszaki Iskola Ada 21

Tóth István – Műszaki Iskola Ada 22

Parciális integrálás Tóth István – Műszaki Iskola Ada 23

A parciális integrálás alkalmazása • A parciális integrálást akkor célszerű használni, ha az integrálandó függvény a következők valamelyike (p(x) egy polinom): Tóth István – Műszaki Iskola Ada 24

Példák Tóth István – Műszaki Iskola Ada 25

Példák Ismételt parciális integrálás: Tóth István – Műszaki Iskola Ada 26

Példák Tóth István – Műszaki Iskola Ada 27

Példák Tóth István – Műszaki Iskola Ada 28

Példák A keresett integrálra vonatkozó egyenlet: Tóth István – Műszaki Iskola Ada 29