A 2 Level Maths Core 4 for Edexcel

A 2 -Level Maths: Core 4 for Edexcel C 4. 2 Coordinate geometry These icons indicate that teacher’s notes or useful web addresses are available in the Notes Page. This icon indicates the slide contains activities created in Flash. These activities are not editable. For more detailed instructions, see the Getting Started presentation. 1 of 29 © Boardworks Ltd 2006

Parametric equations of curves Contents Parametric equations of curves Converting from parametric to Cartesian form The parametric equations of some standard curves The area under a curve defined parametrically Examination-style question 2 of 29 © Boardworks Ltd 2006

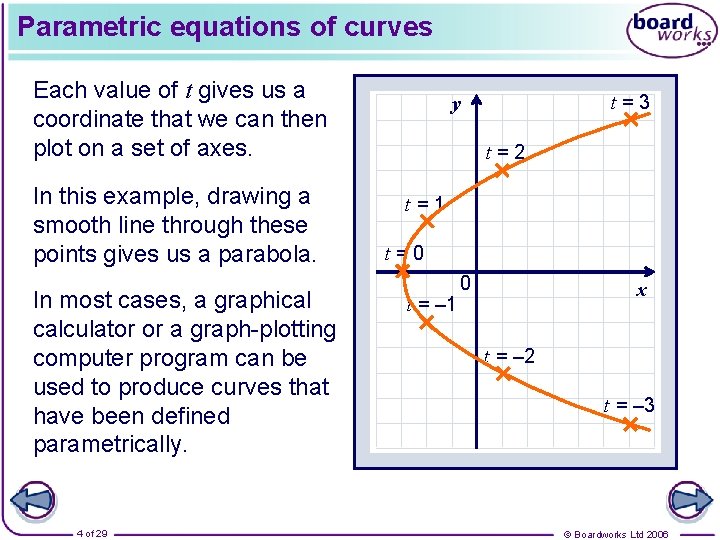
Parametric equations of curves All of the curves we have looked at so far have been defined by a single equation in terms of x and y. Curves can also be defined by writing x and y in terms of a third variable or parameter. For example, using the parameter t a curve is defined by: x = t 2 – 3 y = 2 t We can plot this curve for – 3 < t < 3 using a table of values: t x = t 2 – 3 y = 2 t – 3 – 2 – 1 0 1 2 3 6 – 6 1 – 4 – 2 – 3 0 – 2 2 1 4 6 6 (1, 4) (6, 6) (6, – 6) (1, – 4) (– 2, – 2) (– 3, 0) (– 2, 2) 3 of 29 © Boardworks Ltd 2006

Parametric equations of curves Each value of t gives us a coordinate that we can then plot on a set of axes. In this example, drawing a smooth line through these points gives us a parabola. In most cases, a graphical calculator or a graph-plotting computer program can be used to produce curves that have been defined parametrically. 4 of 29 t=3 y t=2 t=1 t=0 t = – 1 0 x t = – 2 t = – 3 © Boardworks Ltd 2006

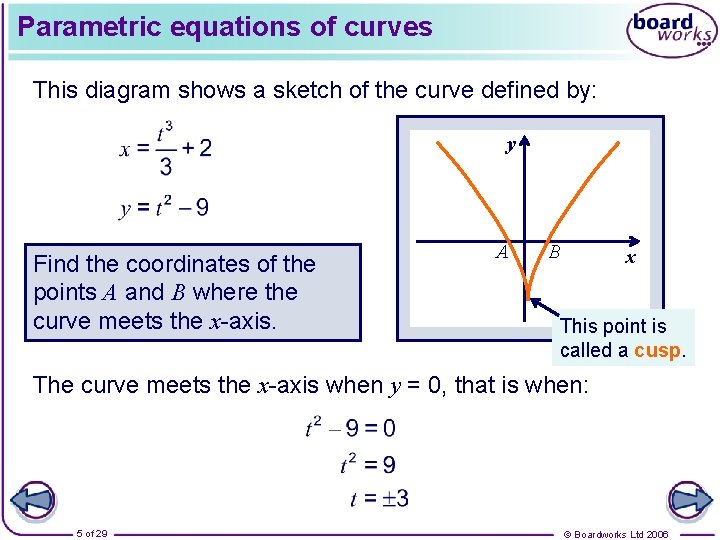
Parametric equations of curves This diagram shows a sketch of the curve defined by: y Find the coordinates of the points A and B where the curve meets the x-axis. A B x This point is called a cusp. The curve meets the x-axis when y = 0, that is when: 5 of 29 © Boardworks Ltd 2006

Parametric equations of curves When t = 3: When t = – 3: So the coordinates of A are (– 7, 0) and the coordinates of B are (11, 0). 6 of 29 © Boardworks Ltd 2006

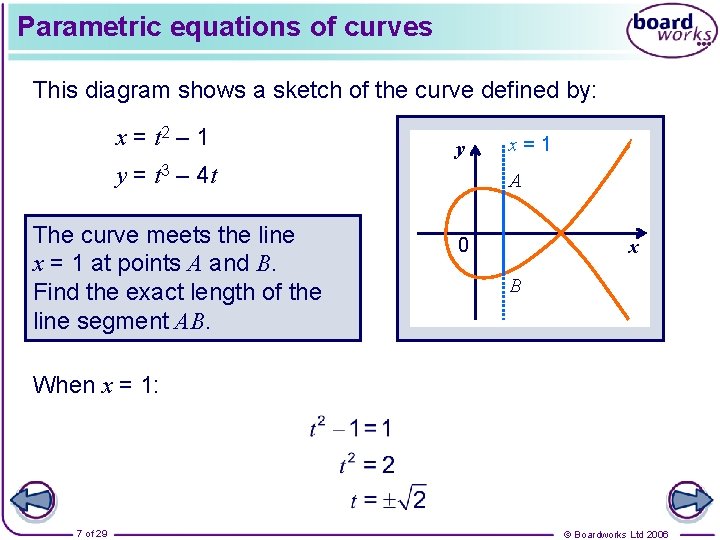
Parametric equations of curves This diagram shows a sketch of the curve defined by: x = t 2 – 1 y y = t 3 – 4 t The curve meets the line x = 1 at points A and B. Find the exact length of the line segment AB. x=1 A 0 x B When x = 1: 7 of 29 © Boardworks Ltd 2006

Parametric equations of curves When t = – : : So the coordinates of A are (1, – ). ) and the coordinates of B The length of line segment AB = 8 of 29 © Boardworks Ltd 2006

From parametric to Cartesian form Contents Parametric equations of curves Converting from parametric to Cartesian form The parametric equations of some standard curves The area under a curve defined parametrically Examination-style question 9 of 29 © Boardworks Ltd 2006

Converting from parametric to Cartesian form The Cartesian form of an equation only contains the two variables x and y. In many cases, a curve that has been defined parametrically can be expressed in Cartesian form by eliminating the parameter. For example, Find the Cartesian equation for the following pair of parametric equations: x = 3 t + 1 y = 5 – 2 t In examples of this type, we make t the subject of one of the equations and then substitute this expression into the other equation. 10 of 29 © Boardworks Ltd 2006

Converting from parametric to Cartesian form If x = 3 t + 1 then Substituting this into the second equation gives: This Cartesian equation represents a straight line graph. 11 of 29 © Boardworks Ltd 2006

Converting from parametric to Cartesian form Find the Cartesian equation for the following pair of parametric equations: x = 5 – t 2 y = 3 t 2 – 4 If x = 5 – t 2 then: The second equation is written in terms of t 2 so we can leave this as it is. Substituting this value of t 2 into the second equation gives: 12 of 29 © Boardworks Ltd 2006

Converting from parametric to Cartesian form Find the Cartesian equation for the following pair of parametric equations: x = 3 + 2 sin θ y = 1 + 2 cos θ We can eliminate the parameter θ using the identity sin 2 θ + cos 2 θ = 1. x – 3 = 2 sin θ y – 1 = 2 cos θ Squaring and adding these equations gives: 13 of 29 © Boardworks Ltd 2006

Converting from parametric to Cartesian form The Cartesian equation is therefore This is the equation of a circle of radius 2 centred at the point (3, 1). Find the Cartesian equation for the following pair of parametric equations: x = 2 cos θ y = cos 2θ Using the double angle formulae we can write: y = 2 cos 2 θ – 1 x 2 = 4 cos 2 θ and so the Cartesian equation is: 14 of 29 © Boardworks Ltd 2006

Contents Parametric equations of standard curves Parametric equations of curves Converting from parametric to Cartesian form The parametric equations of some standard curves The area under a curve defined parametrically Examination-style question 15 of 29 © Boardworks Ltd 2006

Parabolas 16 of 29 © Boardworks Ltd 2006

Rectangular hyperbolae 17 of 29 © Boardworks Ltd 2006

Circles centred at the origin 18 of 29 © Boardworks Ltd 2006

Circles centred at the point (a, b) 19 of 29 © Boardworks Ltd 2006

Ellipses 20 of 29 © Boardworks Ltd 2006

Contents The area under a curve defined parametrically Parametric equations of curves Converting from parametric to Cartesian form The parametric equations of some standard curves The area under a curve defined parametrically Examination-style question 21 of 29 © Boardworks Ltd 2006

The area under a curve defined parametrically We know that the area under the curve y = f(x) between the limits x = a and x = b is given by: Suppose, however, that we wish to find the area under a curve that is defined in terms of a parameter t. We can write the area in terms of the parameter as: where t 1 and t 2 are the limits x = a and x = b rewritten in terms of the parameter t. 22 of 29 © Boardworks Ltd 2006

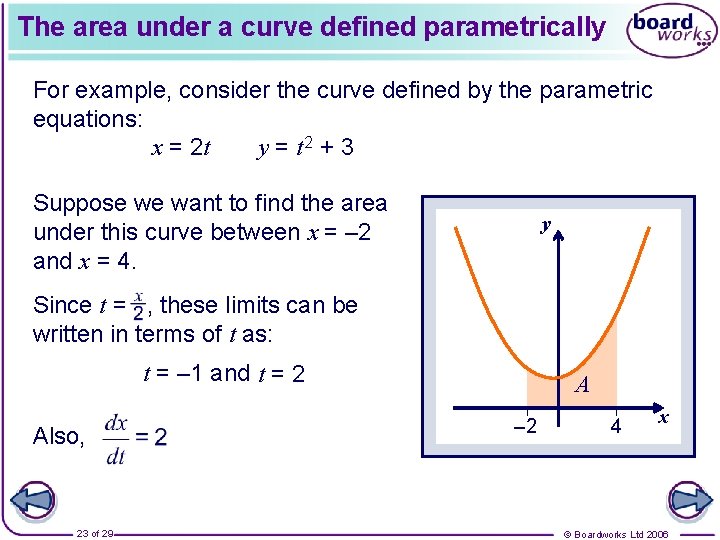
The area under a curve defined parametrically For example, consider the curve defined by the parametric equations: x = 2 t y = t 2 + 3 Suppose we want to find the area under this curve between x = – 2 and x = 4. y Since t = , these limits can be written in terms of t as: t = – 1 and t = 2 Also, 23 of 29 A – 2 4 x © Boardworks Ltd 2006

The area under a curve defined parametrically The area, A, is given by: Substituting t 1 = – 1, t 2 = 2, and y = t 2 + 3 gives: So the required area is 24 units 2. 24 of 29 © Boardworks Ltd 2006

Contents Examination-style question Parametric equations of curves Converting from parametric to Cartesian form The parametric equations of some standard curves The area under a curve defined parametrically Examination-style question 25 of 29 © Boardworks Ltd 2006

Examination-style question The diagram shows part of the curve C, defined by the parametric equations: y y + 3 x = 12 0 The line y + 3 x = 12 cuts the curve C at points A and B. A C x B a) Find the coordinates of the points A and B. b) Show that the Cartesian equation of the curve C is x 2 – y 2 = 16. 26 of 29 © Boardworks Ltd 2006

Examination-style question a) Substituting 27 of 29 and into y + 3 x = 12 gives: © Boardworks Ltd 2006

Examination-style question The line and the curve intersect when t = When t = and when t = 1. : A is the point (4, 0). When t = 1: B is the point (5, – 3). 28 of 29 © Boardworks Ltd 2006

Examination-style question b) Squaring the parametric equations of the curve gives: and Subtracting y 2 from x 2 gives: = 16 29 of 29 © Boardworks Ltd 2006