8 6 Partial Orderings Definition Partial ordering a



























- Slides: 28

8. 6 Partial Orderings

Definition Partial ordering– a relation R on a set S that is Reflexive, Antisymmetric, and Transitive Examples? • R={(a, b)| a is a subset of b } • R={(a, b)| a divides b } on {1, 2, 3, 4} – R={(1, 1), (1, 2), (1, 3), (1, 4), (2, 2), …} • R={(a, b)| a≤ b } • R={(a, b)| a=b+1 }

Partially ordered set (poset) • (S, R) -- a set S and a relation R on S, that is R, A, and T. • Often we use (S, ≼) • Note: ≼ is a generic symbol for R • It includes the usual ≤, but it is more general. It also covers other poset relations: divides, subset, … • We say a ≼ b iff a. Rb • Also a≺b iff a≺ b and a≠b

Examples and non-examples of posets (S, ≼) • 1. (Z, ≤) • 2. (Z, ≥) proof

More examples • 3. (Z, |) where | is “divides” • 4. ( Z+ , |)

…examples • 5. (P(S), � ) where S={1, 2, 3} and P(S) is the power set • 6. (P(S), � ) where S is a set and P(S) is the power set

Comparable • Def: The elements a and b of a poset (S, ≼) are said to be “comparable” if either a ≼b or b ≼a. • Otherwise, they are “incomparable. ”

Comparable, incomparable elements • For each set, find comparable elements 1. (Z, ≤ ) using the usual ≤ 2. (Z+, |) 3. (P(S), ) where S={1, 2, 3} incomparable (if any):

totally (linearly) ordered set • Def: • A poset (S, ≼) is a totally (linearly) ordered set if every two elements of S are comparable. • ≼ is then a total order, and S is a chain.
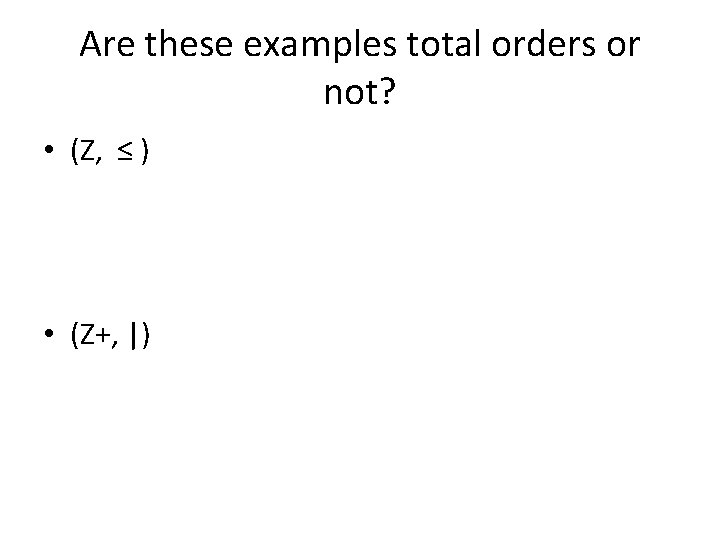
Are these examples total orders or not? • (Z, ≤ ) • (Z+, |)

Lexicographic Order (dictionary) Things to consider: Longer lengths or different lengths in words Ex: Discreet<discrete Discreet<discreetness Discrete<discretion

Lexicographic order • Suppose (A 1, ≼ 1) and (A 2, ≼ 2) are two posets. • Let (a 1, a 2), (b 1, b 2) � A 1 x. A 2 • Let (a 1, a 2) ≺ (b 1, b 2) in case either a 1 ≺ 1 b 1 or (a 1=b 1 and a 2 ≺ 2 b 2) • Letter or number examples

(A 1 x. A 2, ≼) is a poset • Proof Method? • Proof – see book

Hasse diagram • Hasse diagram—a diagram that contains sufficient information to find a partial ordering • Algorithm: – create a digraph with directed edges pointing up – remove all loops (reflexive is assumed) – remove any (a, c) where (a, b) and (b, c) are present (transitivity assumed) – remove arrows (direction up is assumed)

Ex. 1. S={1, 2, 3, 4}; poset (S, ≤) Original digraph reduced diagram 4 | 3 | 2 | 1

Ex. 2: (S, ≼) where S={1, 2, 3, 4, 6, 8, 12} and ≼ ={(a, b)|a divides b} Shorthand: ({1, 2, 3, 4, 6, 8, 12}, | ) 8 12 | | 4 6 | | 2 3 | 1

Ex 3: Hasse diagram of (P({a, b, c}), ) •

Ex. 4: Hasse of ({2, 4, 5, 10, 12, 20, 25, }, | ) •

Maximal, minimal… • Def: • Let (S, ≼) be a poset and a S. – a is maximal in (S, ≼) if there does not exist b � S such that a ≺ b. – a is minimal in (S, ≼) if there does not exist b � S such that b ≺ a. – a is the greatest element of (S, ≼) if b ≼ a for all b � S. – a is the least element of (S, ≼) if a ≼ b for all b � S. • • Find examples of maximal, greatest elements, … in above examples.

greatest element • Claim: The greatest element, when it exists, is unique. • Proof: – Method? • Similarly, the least element, when it exists, is unique.

Upper bound, … • Def: Let (S, ≼) be a poset and A� S. – If u� S and a ≼ u for all a� A, u is an upper bound of A. – If l � S and l ≼ a for all a � A, l is an lower bound of A. – x is a least upper bound of A , lub(A), if x is an upper bound and x ≼ z for every upper bound z of A. – y is a greatest lower bound of A , glb(A), if y is a lower bound and z ≼ y for every lower bound z of A. – Remark: lub and glb are unique when they exist.

Ex. 5 (S, ≼ ) A={b, d, g}, B=(d, e} h i | f | e | c g | d | b a • find lub and glb upper bounds of A: lub(A)= lower bounds of A: glb(A)= upper bounds of B lower bounds of B

Ex. 6: A={4, 6, 8} with “divides” relation lub(A)= glb(A)= Note: lub=? glb=?

Well-ordered set Def: (S, ≼) is well-ordered set if it is a poset such that ≼ is a total ordering and every nonempty subset of S has a least element. Find Ex and non-ex. : • (Z+, ≤) • (Z+ x Z+, lexicographic order) • (R+, ≤)

Topological sorting Use: for project ordering Def: A total ordering ≼ is compatible with the partial order R if a ≼ b whenever a. Rb. The construction of such a total order is called a topological sorting. Lemma: Every finite non-empty poset (S, ≼ ) has a minimal element.

({2, 4, 5, 10, 12, 20, 25}, | ) Recall Hasse diagram for ({2, 4, 5, 10, 12, 20, 25}, | ) Create several topological sorts.

House Ex- book •

Advising example •
 Parsial atau partial
Parsial atau partial Topological ordering
Topological ordering Representing comparing and ordering decimals
Representing comparing and ordering decimals Questions on recurring decimals
Questions on recurring decimals Binary ordering algorithm
Binary ordering algorithm Eakrt
Eakrt Ordering adjectives
Ordering adjectives Annual ordering cost formula
Annual ordering cost formula Formula for eoq
Formula for eoq Formula for eoq
Formula for eoq Cisco ise ordering
Cisco ise ordering Message ordering paradigms
Message ordering paradigms Spatial sequence examples
Spatial sequence examples Hypothesis space in machine learning
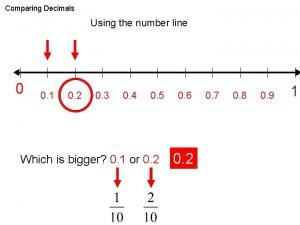
Hypothesis space in machine learning Ordering decimals on a number line
Ordering decimals on a number line Ordering rational numbers examples
Ordering rational numbers examples Ordering integers examples
Ordering integers examples How to compare real numbers
How to compare real numbers Causal order in distributed system
Causal order in distributed system Independent
Independent Coffee ordering app in android studio
Coffee ordering app in android studio Ordering rational numbers examples
Ordering rational numbers examples Time clocks and the ordering of events
Time clocks and the ordering of events Real time ordering
Real time ordering Ordering fractions decimals and percentages
Ordering fractions decimals and percentages Event ordering
Event ordering Ordering a meal in a restaurant dialogue
Ordering a meal in a restaurant dialogue Time clocks and the ordering of events
Time clocks and the ordering of events The source document for all cash payments is a check
The source document for all cash payments is a check