Partial Orderings Partial Orderings A relation R on

Partial Orderings

Partial Orderings A relation R on a set S is called a partial orderingif it is: reflexive antisymmetric transitive A set S together with a partial ordering R is called a partially ordered set , or poset, and is denoted by (S, R). Example: “ ” is a partial ordering on the set of integers reflexive: a a for every integer a anti-symmetric: If a b and b a then a = b transitive: a b and b c implies a c Therefore “ ” is a partial ordering on the set of integers and (Z, ) is a poset.

Comparable/Incomparable Elements Let “≼” denote any relation in a poset (e. g. ) The elements a and b of a poset (S, ≼) are: comparableif either a≼b or b≼a incomparableif neither a≼b nor b≼a Example: Consider the poset (Z+, │), where “a│b” denotes “a divides b” 3 and 9 are comparable because 3│9 5 and 7 are not comparable because nether 5⫮ 7 nor 7⫮ 5

Partial and Total Orders If some elements in a poset (S, ≼) are incomparable, then it is partially ordered ≼ is a partial order If every two elements of a poset (S, ≼) are comparable, then it is totally orderedor linearly ordered ≼ is a total (or linear) order Examples: (Z+, │) is not totally ordered because some integers are incomparable (Z, ≤) is totally ordered because any two integers are comparable (a ≤ b or b ≤ a)

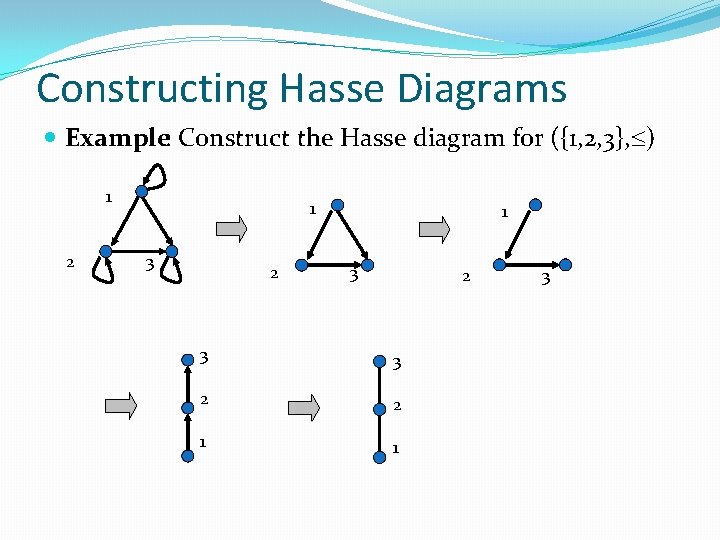
Hasse Diagrams Graphical representationof a poset It eliminates all implied edges (reflexive, transitive) Arranges all edges to point up (implied arrow heads) Algorithm: Start with the digraph of the partial order Remove the loops at each vertex (reflexive) Remove all edges that must be present because of the transitivity Arrange each edge so that all arrows point up Remove all arrowheads

Constructing Hasse Diagrams Example: Construct the Hasse diagram for ({1, 2, 3}, ) 1 2 1 3 2 3 3 2 2 1 1 3

Maximal and minimal Elements Let (S, ≼) be a poset a is maximalin (S, ≼) if there is no b S such that a≼b a is minimal in (S, ≼) if there is no b S such that b≼a a is the greatestelement of (S, ≼) if b≼a for all b S a is the least element of (S, ≼) if a≼b for all b S greatest and least must be unique h j g f d e b c a Example: • Maximal: h, j • Minimal: a • Greatest element: None • Least element: a

Upper and Lower Bounds Let A be a subset of (S, ≼) If u S such that a≼u for all a A, then u is an upper bound of A If x is an upper bound of A and x≼z whenever z is an upper bound of A, then x is the least upper boundof A (must be unique) Analogous for lower bound and greatest upperbound h j g f d e b c a Example: let A be {a, b, c} • Upper bounds of A: e, f, j, h • Least upper bound of A: e • Lower bound of A: a • Greatest lower bound of A: a