5 Hypergeometric Functions Chap 7 Hypergeometric equation Gauss

5. Hypergeometric Functions Chap 7: Hypergeometric equation ( Gauss’ ODE & functions ) Regular singularities at Hypergeometric function (series) Solution : Pochhammer symbol For a, b, c real, range of convergence are : Series diverges for

Properties Sum terminates if 2 F 1 includes many elementary functions. E. g. 2 F 1 = polynomial

2 nd Solution, Alternative ODE § 7. 6 : 2 nd Solution : c = integer Alternative ODE : y not independent of additional logarithm term required 2 F 1 ( a, b ; c ; x)

Contiguous Function Relations

Hypergeometric Representations

6. Confluent Hypergeometric Functions Confluent Hypergeometric eq. Singularities : regular at irregular at Solution : For a, c real, series converge for all finite x. Sum terminates if E. g. 1 F 1 = polynomial

2 nd solution : Standard form : Alternate ODE :

Integral Representations Techniques for verifying integral representations : 1. g(x, t) or Rodrigues relations. 2. Expand integrand into series & integrate. 3. (a) As solution to ODE. (b) Check normalization.

Confluent Hypergeometric Representations

Further Observations Advantages for using the (confluent) hypergeometric representations : 1. Asymptotic behavior or normalization easier to evaluate via the integral representation of M & U. 2. Inter-relationship between special functions becomes clearer. Self-adjoint version : Whittaker function Self-adjoint ODE : 2 nd solution :

7. Dilogarithm Usage : 1. Matrix elements in few-body problems in atomic physics. 2. Perturbation terms in electrodynamics.

Expansion Poly-logarithm

Analytic Properties Branch point at z = 1. Conventional choice : Branch cut from z = 1 to z = . with principal value : For series converges & is real. For series diverges but integral is finite & complex ( analytic continued ). For series diverges but integral is finite & real ( analytic continued ).

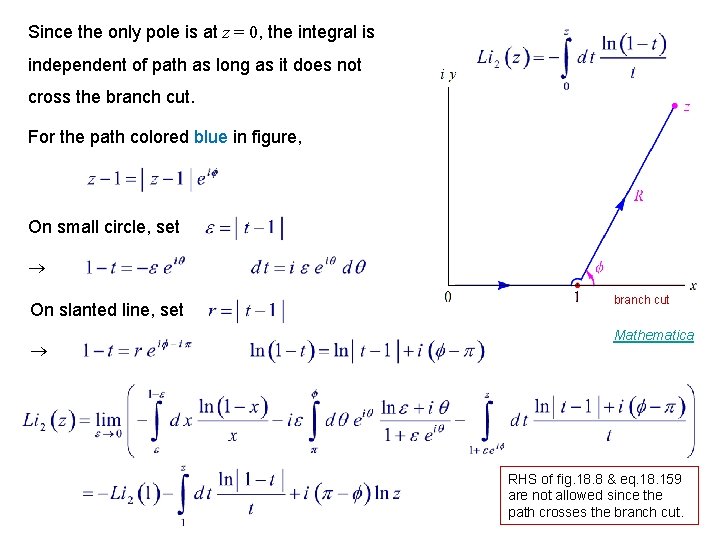
Since the only pole is at z = 0, the integral is independent of path as long as it does not cross the branch cut. For the path colored blue in figure, On small circle, set On slanted line, set branch cut Mathematica RHS of fig. 18. 8 & eq. 18. 159 are not allowed since the path crosses the branch cut.

Properties & Special Values generates Li 2 for all x from those in | x | 1/2. e. g. Proof : ¢ both sides & find identity. Set z = 0 or 1 to determine const.

Example 18. 7. 1. Check Usefulness of Formula Question: Are the individual terms real? I real & converges if Li 2(x) is real for x < 1 is real both Li 2 terms are real.

8. Elliptic Integrals Example 18. 8. 1. Period of Simple Pendulum Period

Definitions Elliptic integral of the 1 st kind Complete Elliptic integral of the 1 st kind

Elliptic integral of the 2 nd kind Complete Elliptic integral of the 1 st kind

Series Expansions Ex. 13. 3. 8 Ex. 18. 8. 2

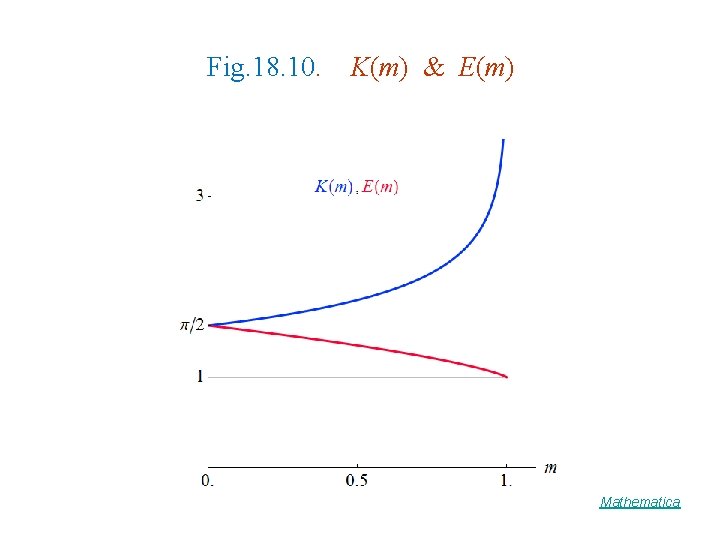
Fig. 18. 10. K(m) & E(m) Mathematica

Limiting Values Integrals of the following form can be expressed in terms of elliptic integrals. E. Jahnke & F. Emde, “Table of Higher Functions”