5 Solusi Persamaan Linier Eliminasi Gauss Eliminasi Gauss

5. Solusi Persamaan Linier Eliminasi Gauss, Eliminasi Gauss Jordan, Iterasi Jacobi Iterasi Seidell, Dekomposisi Crout & Dekomposisi Cholesky

Pendahuluan l Sistem Linier (sistem banyak variabel) memiliki persamaan umum : l Dalam bentuk perkalian matrik menjadi : A x b

Eliminasi Gauss ? Solusinya menjadi : Sekali xn, xn-1, xn-2, …, xk+1 diketahui , maka nilai xk dapat dihitung dengan : Dengan k = n-1, n-2, …, 1 dan akk <> 0

Penyulihan Mundur dalam Pascal Procedure sulih_mundur(A : matriks; b : vektor; n : integer; var x : vektor) Var j, k : integer; sigma : real; begin x[n]: =b[n]/a[n, n] for k: =n-1 downto 1 do begin for j: =k+1 to n do sigma: =sigma + a[k, j] * x[j]; x[k]: =(b[k]-sigma)/a[k, k]; end;

Eliminasi Gauss (Cont. ) ? l l l = Tanda pangkat (1), (2), (3), …. dst menunjukkan banyaknya modifikasi yang telah dilakukan terhadap nilai tersebut. Proses eliminasi terdiri dari 3 operasi mendasar terhadap baris, berupa : – Pertukaran – Penskalaan ( mengalikan satu baris dengan bilangan bukan nol) – Penggantian ( mengganti satu baris dengan hasil operasi perkalian baris lain ), dengan persamaan : barisr = barisr – mp, rbarisp Elemen ar, r pada posisi (r, r) digunakan untuk eliminasi xr pada baris r+1, r+2, …N dinamakan elemen pivot sehingga mp, r = nilai pada baris p / elemen pivot

Eliminasi Gauss (Cont. ) l Contoh : l Solusi :

Eliminasi Gauss (Cont. ) pivot bernilai nol diatasi dengan Strategi Pivoting : jika app(p-1) = 0, cari baris k yang ak, p <>0 dan k>p, kemudian pertukarkan baris p dengan baris k l

Eliminasi Gauss (Cont. )

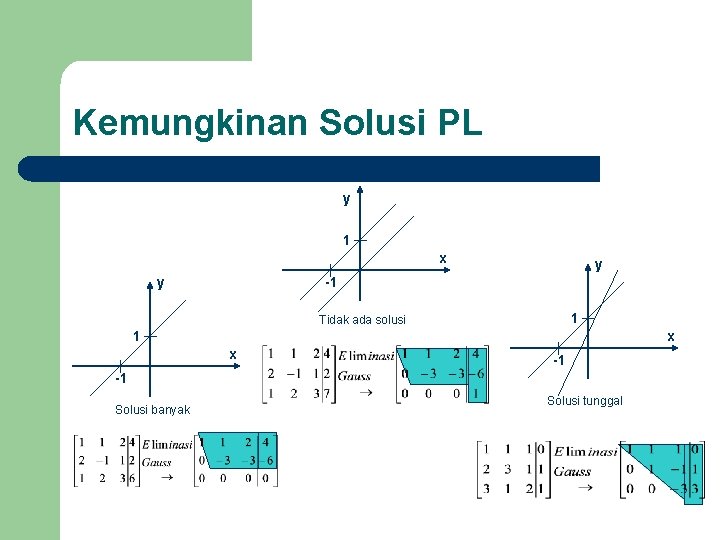
Kemungkinan Solusi PL y 1 x y y -1 1 Tidak ada solusi 1 x x -1 -1 Solusi banyak Solusi tunggal

Eliminasi Gauss Jordan l Format matrik mengalami perubahan : Ax = b Ix =b’ l Matrik A bersamaan dengan vektor b dieliminasi sampai matrik A menjadi matrik Identitas solusinya : x 1 = b 1’, x 2 = b 2’, …. . xn = bn’ l

Iterasi Jacobi & Seidell akk <> 0, k = 1, 2, 3, …, n Jacobi Gauss-Seidell

Iterasi Jacobi & Seidell (Cont. ) tebakkan awal : kondisi berhenti iterasi : untuk semua I = 1, 2, 3, …, n syarat cukup agar iterasinya konvergen adalah sistem dominan secara diagonal

Iterasi Jacobi & Seidell (Cont. ) l Contoh Soal :

Dekomposisi Crout l terdiri dari 2 langkah utama : – – l eliminasi maju subtitusi mundur penurunan rumus : – – – matrik A didekomposisi menjadi matrik L dan U matrik U adalah matrik segitiga atas matrik L adalah matrik segitiga bawah dengan elemen diagonalnya = 1

Dekomposisi Crout (Cont. )

Dekomposisi Crout (Cont. )

Dekomposisi Cholesky l l l dapat dilakukan untuk kasus A = AT susun matrik A = LLT dengan formula pembentuk elemen L :

Dekomposisi Cholesky (Cont. ) l Contoh kasus