Gauss Seidel Dr Mario Gonzlez Cardel Gauss Seidel

Gauss – Seidel. Dr. Mario González Cardel

Gauss - Seidel Análisis Numérico • El método de Gauss – Seidel es un método de aproximaciones sucesivas, el cual, como todos los métodos iterativos, se basa en la aplicación de una fórmula de recurrencia.

Gauss - Seidel Análisis Numérico • Supongamos que tenemos un sistema de ecuaciones como sigue:

Gauss - Seidel Análisis Numérico • Deseamos conocer los valores de xi con i = 1, 2, 3, . . . , n. Entonces despejamos x 1 de la primera ecuación, x 2 de la segunda y así sucesivamente:

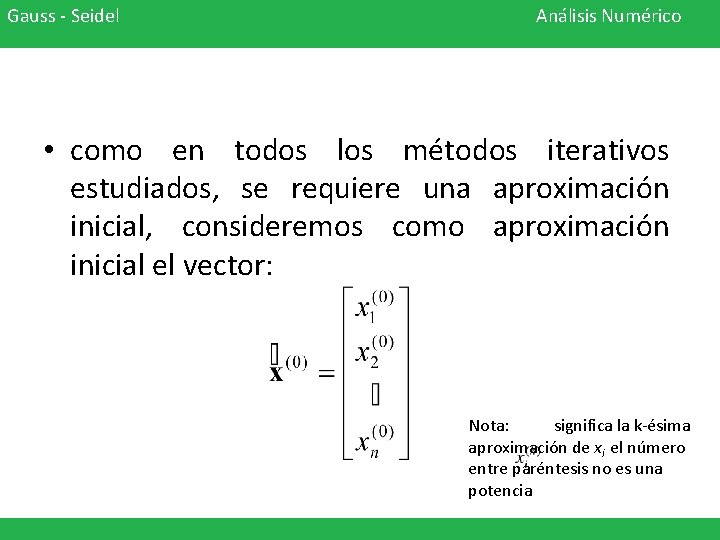
Gauss - Seidel Análisis Numérico • como en todos los métodos iterativos estudiados, se requiere una aproximación inicial, consideremos como aproximación inicial el vector: Nota: significa la k-ésima aproximación de xi el número entre paréntesis no es una potencia

Gauss - Seidel Análisis Numérico • al sustituir en la expresión para x 1 nos da una mejor aproximación de x 1.

Gauss - Seidel Análisis Numérico • Al calcular x 2 ya conocemos una mejor aproximación de x 1, puede utilizarse en la expresión para x 2, , es decir que x 2 se aproxima por:

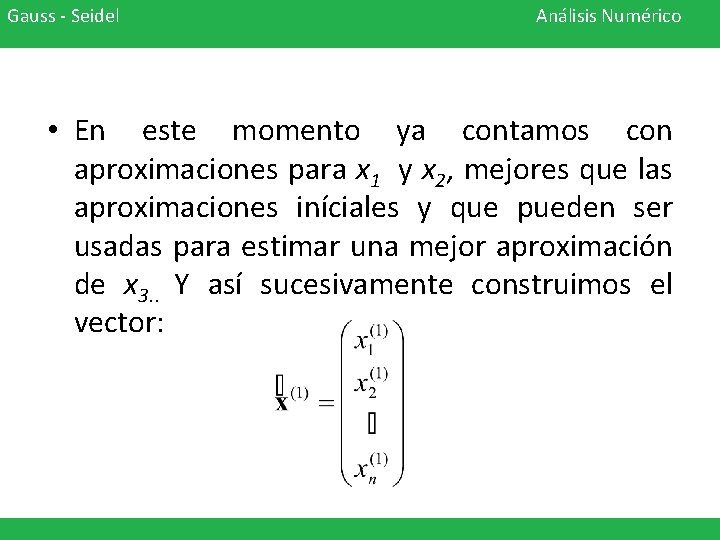
Gauss - Seidel Análisis Numérico • En este momento ya contamos con aproximaciones para x 1 y x 2, mejores que las aproximaciones iníciales y que pueden ser usadas para estimar una mejor aproximación de x 3. . Y así sucesivamente construimos el vector:

Gauss - Seidel Análisis Numérico • Por lo que las expresiones de recurrencia quedan como sigue:

Gauss - Seidel Análisis Numérico • Cómo en todos los métodos numéricos de aproximaciones sucesivas surgen tres preguntas: • ¿Cuál es la aproximación inicial? • La mejor aproximación inicial es:

Gauss - Seidel Análisis Numérico • ¿Hasta cuándo iteramos? • Detenemos el proceso de iteración cuando la diferencia absoluta entre dos aproximaciones consecutivas sea menor a un valor previamente fijado, pero ahora debemos considerar todas y cada una de las componentes del vector que aproxima a la solución. Matemáticamente esto se escribe así:

Gauss - Seidel Análisis Numérico • Matemáticamente esto se escribe así: • O bien: para i = 1, 2, 3, . . . , n.

Gauss - Seidel Análisis Numérico • ¿Siempre converge? • Por lo tanto el método de Gauss - Seidel converge cuando es aplicado a sistemas de ecuaciones cuya matriz asociada es Diagonalmente dominantes. • Es decir:

Gauss - Seidel Análisis Numérico Ventajas y Desventajas • Converge rápidamente. • Es muy fácil de programar. • Resuelve sistema grandes • Si la matriz asociada es diagonalmente dominante se garantiza que el método de Gauss – Seidel converge, pero cuando no lo es, no existe garantía de la divergencia del método.

Gauss - Seidel Análisis Numérico Ejemplo: • Utilizando el método de Gauss - Seidel resolver con un error menor a 0. 0001 el siguiente sistema de ecuaciones:

Gauss - Seidel Análisis Numérico • Verifiquemos si cumple el criterio de convergencia: Para el renglón 1 |3| + |-5| < |12| El renglón 2 |3| + |-3| < |-8| Renglón 3 |5| + |4| < |-12|

Gauss - Seidel Análisis Numérico Resolución: • Despejamos a x 1 de la primera ecuación; x 2 de la segunda y x 3 de la tercera:

Gauss - Seidel Análisis Numérico • por lo que las expresiones de recurrencia son:

Gauss - Seidel Análisis Numérico • Tomando como aproximación inicial:

Gauss - Seidel Análisis Numérico • calculamos los valores de cada componente de esto es:

Gauss - Seidel Análisis Numérico • Por lo tanto la primera aproximación a la solución es el vector • Y el error:

Gauss - Seidel Análisis Numérico • Cálculo para la segunda aproximación:

Gauss - Seidel • La segunda aproximación es: • Y el error es: Análisis Numérico

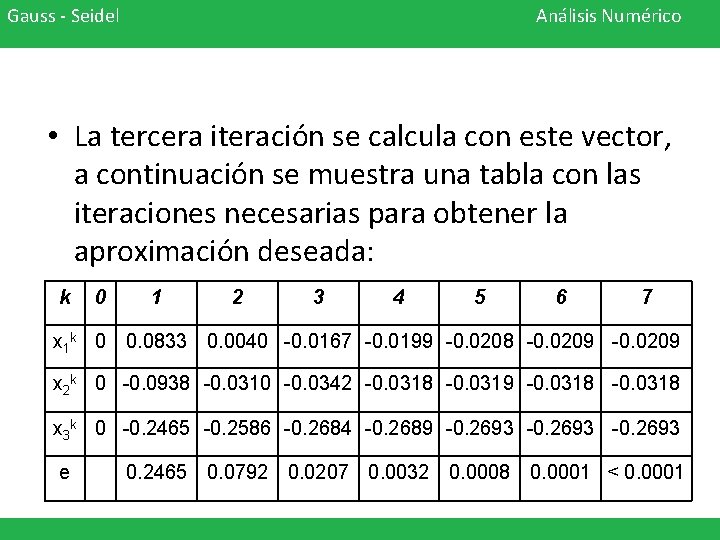
Gauss - Seidel Análisis Numérico • La tercera iteración se calcula con este vector, a continuación se muestra una tabla con las iteraciones necesarias para obtener la aproximación deseada: k 0 x 1 k 0 1 2 3 4 5 6 7 0. 0833 0. 0040 -0. 0167 -0. 0199 -0. 0208 -0. 0209 x 2 k 0 -0. 0938 -0. 0310 -0. 0342 -0. 0318 -0. 0319 -0. 0318 x 3 k 0 -0. 2465 -0. 2586 -0. 2684 -0. 2689 -0. 2693 e 0. 2465 0. 0792 0. 0207 0. 0032 0. 0008 0. 0001 < 0. 0001

Gauss - Seidel Análisis Numérico • Una buena aproximación a la solución es: • x 1 = -0. 0209 ± 0. 0001 • x 2 = -0. 0319 ± 0. 0001 • x 3 = -0. 2693 ± 0. 0001.

Gauss - Seidel Análisis Numérico • Comprobando: Lo que satisface al sistema con un error menor al 0. 004%

Gauss - Seidel Análisis Numérico Conclusión: • El método de Gauss - Seidel es un método numérico de aproximaciones sucesivas, que converge rápidamente siempre que la matriz asociada del sistema sea diagonalmente dominante. • Con este método se pueden resolver sistemas de un gran número de ecuaciones

Factores Cuadráticos Análisis Numérico Grupo 29 Método de Gauss - Seidel Facultad de Ingeniería UNAM