5 2 Centripetal acceleration and force Centripetal acceleration

5. 2 Centripetal acceleration and force • Centripetal acceleration • Centripetal force experiment © Manhattan Press (H. K. ) Ltd. 1

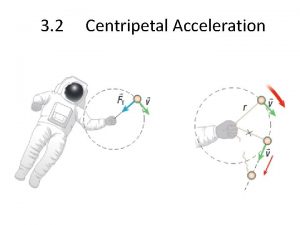
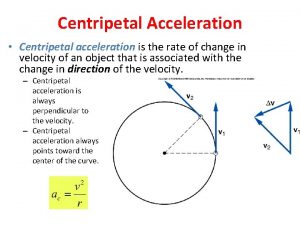
5. 2 Centripetal acceleration and force (SB p. 170) Centripetal acceleration Change in velocity ( v) = v. B – v. A (represented by QR) Go to Common Error Particle experiences change of velocity (acceleration) along direction AO (pointing to Go to centre of circle) centripetal acceleration Common Error © Manhattan Press (H. K. ) Ltd. 2

5. 2 Centripetal acceleration and force (SB p. 170) Centripetal acceleration An object in uniform circular motion experiences a centripetal acceleration which is the acceleration directed towards the centre of the circle. © Manhattan Press (H. K. ) Ltd. 3

5. 2 Centripetal acceleration and force (SB p. 171) Centripetal acceleration pointing to centre of circle © Manhattan Press (H. K. ) Ltd. Go to Common Error 4

5. 2 Centripetal acceleration and force (SB p. 171) Centripetal force Steady speed v but changing direction of motion - force acting on it (Newton’s 1 st Law) No force in direction of motion (constant speed) Force towards centre of circular path centripetal force (Fc) Go to Common Error © Manhattan Press (H. K. ) Ltd. 5

5. 2 Centripetal acceleration and force (SB p. 172) Centripetal force Note: For a uniform circular motion: 1. Centripetal force is always perpendicular to the motion of the body. It does no work on the body and the kinetic energy of the body remains unchanged. © Manhattan Press (H. K. ) Ltd. 6

5. 2 Centripetal acceleration and force (SB p. 172) Centripetal force Note: 2. The centripetal force (Fc) is the force required to keep the body moving in a circle. It is provided by the external resultant force towards the centre. It is a functional name rather than a real force. The origins of the centripetal forces may be tension, friction or reaction forces. © Manhattan Press (H. K. ) Ltd. 7

5. 2 Centripetal acceleration and force (SB p. 172) Centripetal force experiment 1. Procedure - rubber bung whirled around in horizontal circle - measure time taken for 50 revolutions of bung - calculate angular velocity ( ) © Manhattan Press (H. K. ) Ltd. 8

5. 2 Centripetal acceleration and force (SB p. 173) Centripetal force experiment 2. Analysis T cosθ = mg. . . (1) T sinθ = mr 2. . . (2) T sinθ = m (l sinθ) 2 T = ml 2 T is provided by Mg Fc = mr 2 © Manhattan Press (H. K. ) Ltd. 9

5. 2 Centripetal acceleration and force (SB p. 173) Centripetal force experiment 3. Error (i) there is a friction acting at the opening of the glass tube, (ii) the string is not inextensible, Go to (iii) the rubber bung is not whirled Example 3 with constant speed, and (iv) the rubber bung is not whirled in a horizontal circle. © Manhattan Press (H. K. ) Ltd. Go to Example 4 10

End © Manhattan Press (H. K. ) Ltd. 11

5. 2 Centripetal acceleration and force (SB p. 170) When a particle moves in uniform circular motion, it has constant speed but not constant velocity because its direction changes from time to time. Return to © Manhattan Press (H. K. ) Ltd. Text 12

5. 2 Centripetal acceleration and force (SB p. 170) Uniform circular motion is not a kind of uniformly accelerated motion since the acceleration is fixed only in magnitude, but not in direction. Return to © Manhattan Press (H. K. ) Ltd. Text 13

5. 2 Centripetal acceleration and force (SB p. 171) As centripetal acceleration (a) may be expressed as It is wrong to think that Since velocity is not a constant and v r. Therefore, Return to Text Centripetal acceleration is actually increased with radius r. © Manhattan Press (H. K. ) Ltd. 14

5. 2 Centripetal acceleration and force (SB p. 171) The circular motion does not produce a centripetal force. The fact is that the centripetal force that causes the circular motion is actually a resultant of other forces. Return to Text © Manhattan Press (H. K. ) Ltd. 15

5. 2 Centripetal acceleration and force (SB p. 173) Q: (a) In the centripetal force experimentioned above, what will happen when the string breaks while the bung is whirling? (b) What is the relationship between the vertical angle θ of the string and the speed of the bung? (c) Explain with the aid of a diagram, why a mass at the end of a light inelastic string cannot be whirled in circle in air with the string horizontal. Solution © Manhattan Press (H. K. ) Ltd. 16

5. 2 Centripetal acceleration and force (SB p. 174) Solution: (a) If the string breaks, the centripetal force disappears. The bung can no longer keep in the circular motion. It will fly away tangentially. (b) ∴ The angle θ increases as the bung is whirled at a higher speed. Go to More to Know 1 © Manhattan Press (H. K. ) Ltd. 17

5. 2 Centripetal acceleration and force (SB p. 174) Solution (cont’d): (c) If the string is horizontal (Fig. (a)), there is no vertical force to balance the weight of the mass mg. Therefore, the string must make an angle θ with the vertical (Fig. (b)) so that the vertical component of T counteracts the weight mg. T cosθ = mg Fig. (a) © Manhattan Press (H. K. ) Ltd. Fig. (b) Return to Text 18

5. 2 Centripetal acceleration and force (SB p. 174) 1. The equation tanθ = is very useful in answering questions about circular motion. 2. The vertical angle θ is independent of the mass m. 3. A specific vertical angle θ is ideal for one speed only. Return to © Manhattan Press (H. K. ) Ltd. Text 19

5. 2 Centripetal acceleration and force (SB p. 174) Q: (a) A pendulum bob moves in a horizontal circle with constant angular velocity as shown in the figure. Find, in terms of m, , l and g, (i) the centripetal force acting on the bob, (ii) the tension T in the string, and (iii) the angle θ. © Manhattan Press (H. K. ) Ltd. 20

5. 2 Centripetal acceleration and force (SB p. 175) Q: (b) A student suggests that the value of g can be determined by measuring the period t of the revolution of the bob for various values of θ. (i) Find an expression for t in terms of l, g and θ. (ii) Suggest a graph which could be used to obtain the value of g. (iii) Discuss critically whether this is a good method for the determination of g. Solution © Manhattan Press (H. K. ) Ltd. 21

5. 2 Centripetal acceleration and force (SB p. 175) Solution : (a) (i) Centripetal force (Fc) = mr 2 = ml sinθ 2 (ii) Horizontal component of T, T sinθ = Fc = ml sinθ 2 ∴ T = ml 2 (iii) Vertical component of T, © Manhattan Press (H. K. ) Ltd. 22

5. 2 Centripetal acceleration and force (SB p. 175) Solution (cont’d) : (iii) It is not a good method of determining g because it is difficult to maintain the angle θ at a fixed value, and it is difficult to measure the angle θ. Return to © Manhattan Press (H. K. ) Ltd. Text 23