Centripetal Acceleration and Centripetal Force Circular Motion When
































- Slides: 51

Centripetal Acceleration and Centripetal Force

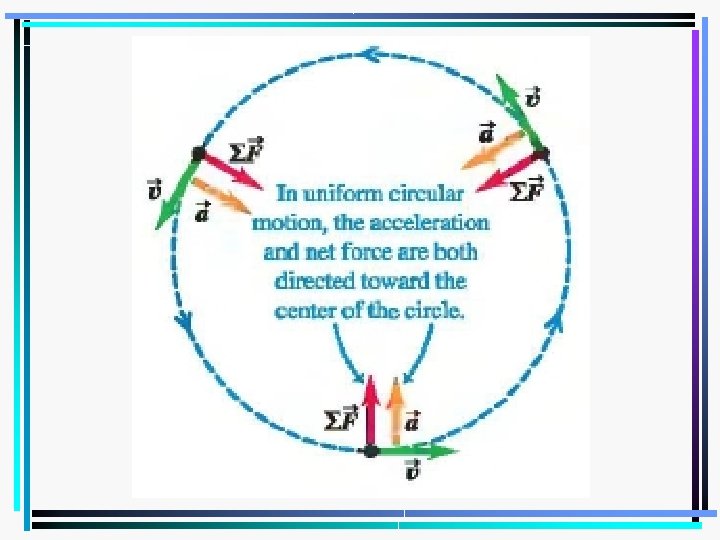
Circular Motion • When an object moves in a circle at constant speed, we describe it as undergoing uniform circular motion. • Its speed is constant, but its velocity is not because velocity includes direction and the object’s direction is clearly changing.

Circular Motion • A changing velocity means acceleration. • The pull on the string is always directed perpendicular to the velocity. • The pull accelerates the ball into a circular path, even though the ball does not speed up or slow down. • The pull changes only the direction of the velocity, not the magnitude.


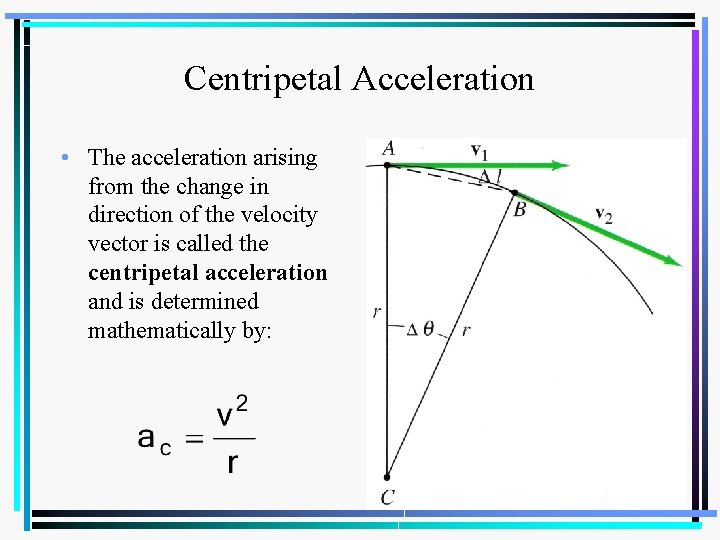
Centripetal Acceleration • The acceleration arising from the change in direction of the velocity vector is called the centripetal acceleration and is determined mathematically by:

Centripetal Acceleration • Centripetal means center-seeking. • Centripetal acceleration is always directed toward the center of the circle of motion. • It is this centripetal acceleration that is responsible for the change in the direction of the velocity; the magnitude of the velocity remains constant. • Any change in the tangential acceleration causes a change in the speed of the particle as it travels around the circle. In uniform circular motion, a. T = 0, so the acceleration is completely radial (ar) or centripetal.

Centripetal Force • Newton’s Second Law explains that an object undergoing acceleration is experiencing a net force. The net force on an object undergoing uniform circular motion is called the centripetal force Fc. • The centripetal force necessary for an object of mass m to travel with constant speed v in a circle of radius r is given by:

Centripetal Force • The centripetal force always points toward the center of the circle about which the object moves with uniform speed. • If the centripetal force applied to the object is removed, the object will move in a straight-line tangent to the curved path at the point where the centripetal force ceases. When the centripetal force ceases, the object has no unbalanced forces acting upon it and thus moves in a straight line at constant speed.

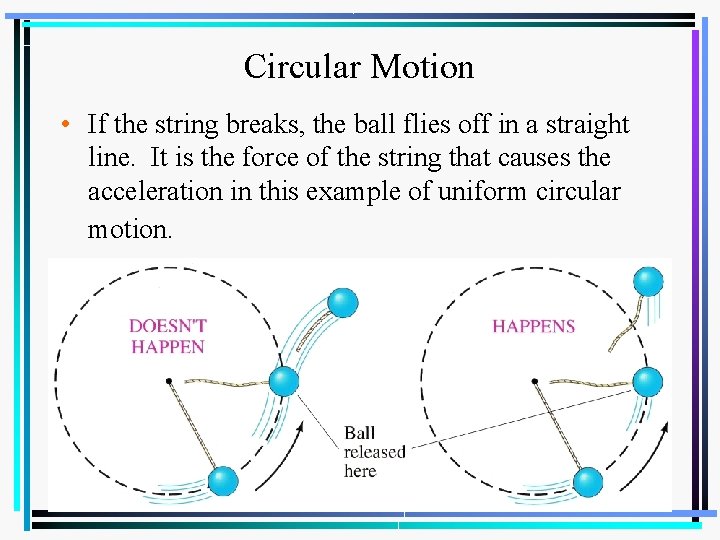
Circular Motion • If the string breaks, the ball flies off in a straight line. It is the force of the string that causes the acceleration in this example of uniform circular motion.

Centripetal Force • Centripetal force is the name given to any force that is directed at right angles to the path of a moving object and that tends to produce circular motion. • Examples: – the gravitational force directed toward the center of the Earth holds the Moon in an almost circular orbit about the Earth; – an electromagnetic force that is directed toward the nucleus holds the electrons that revolve about the nucleus of the atom. • Directions in centripetal force problems: – Positive direction is inwards toward center of circle. – Negative direction is outward away from center of circle.

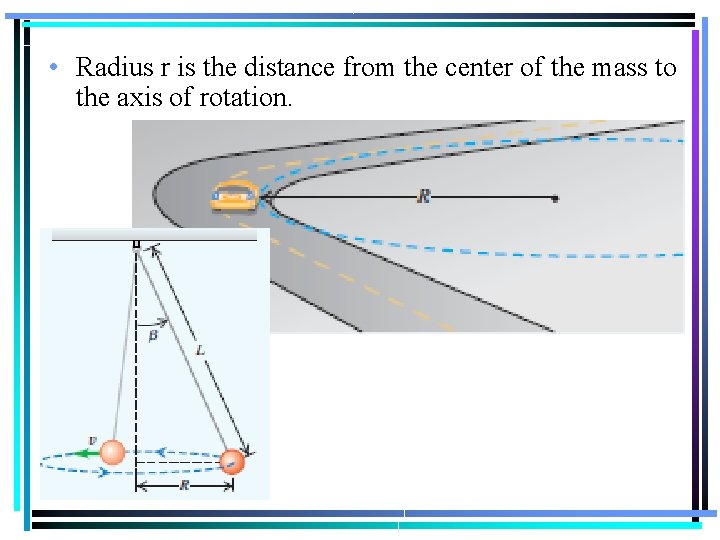
• Radius r is the distance from the center of the mass to the axis of rotation.

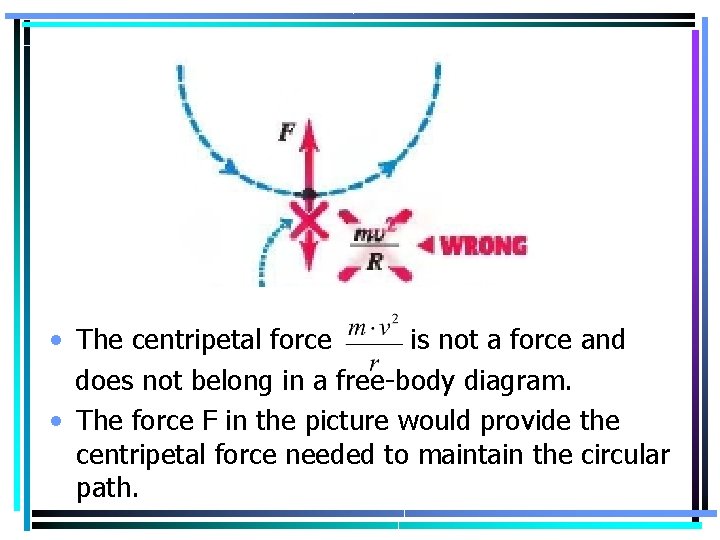
• The centripetal force is not a force and does not belong in a free-body diagram. • The force F in the picture would provide the centripetal force needed to maintain the circular path.

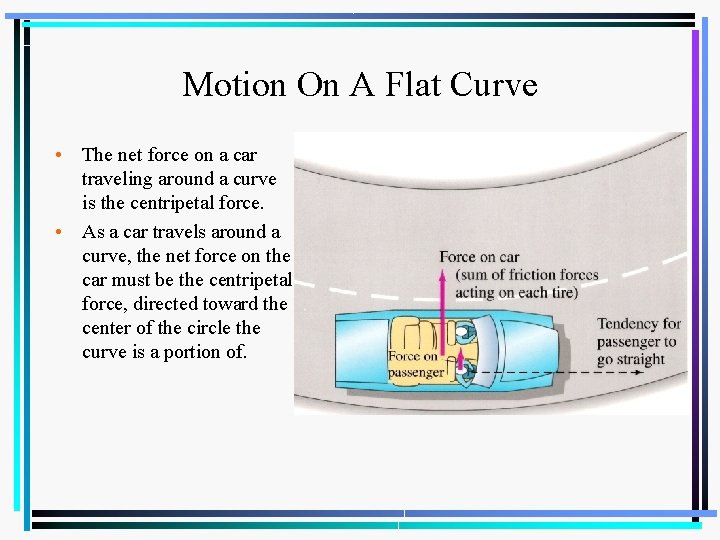
Motion On A Flat Curve • The net force on a car traveling around a curve is the centripetal force. • As a car travels around a curve, the net force on the car must be the centripetal force, directed toward the center of the circle the curve is a portion of.

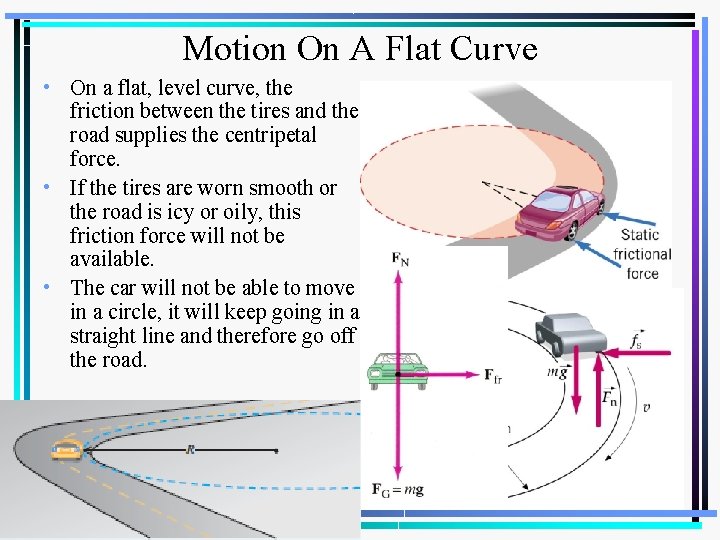
Motion On A Flat Curve • On a flat, level curve, the friction between the tires and the road supplies the centripetal force. • If the tires are worn smooth or the road is icy or oily, this friction force will not be available. • The car will not be able to move in a circle, it will keep going in a straight line and therefore go off the road.

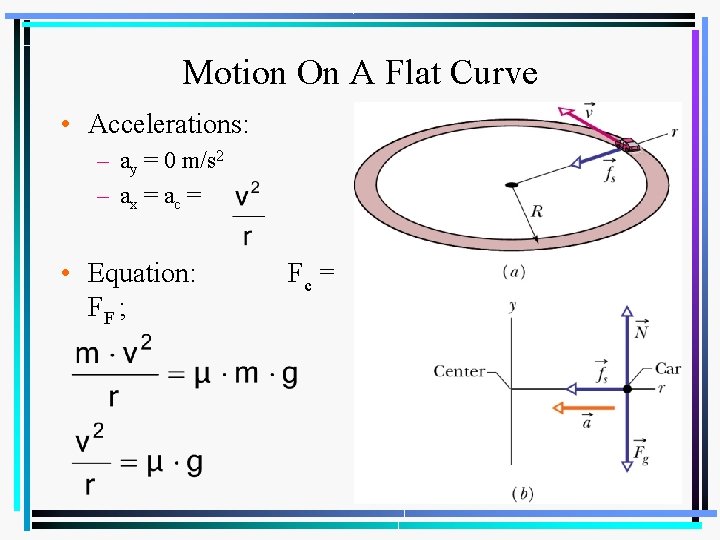
Motion On A Flat Curve • Accelerations: – ay = 0 m/s 2 – ax = a c = • Equation: FF ; Fc =

Motion On A Banked Curve • Some curves are banked to compensate for slippery conditions. • In addition to any friction forces that may or may not be present, the road exerts a normal force perpendicular to its surface. • The downward force of the car’s weight is also present. • These two forces add as vectors to provide a net force Fnet that points toward the center of the circle; this is the centripetal force. • The centripetal force is directed toward the center of the circle, it is not parallel to the banked road.

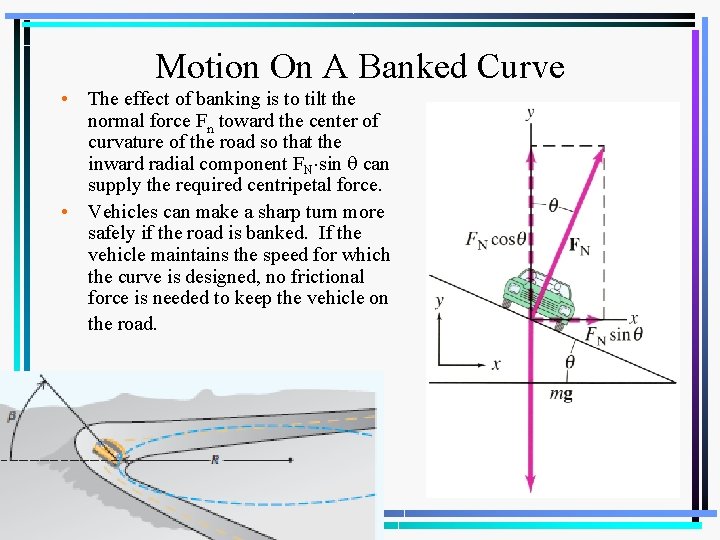
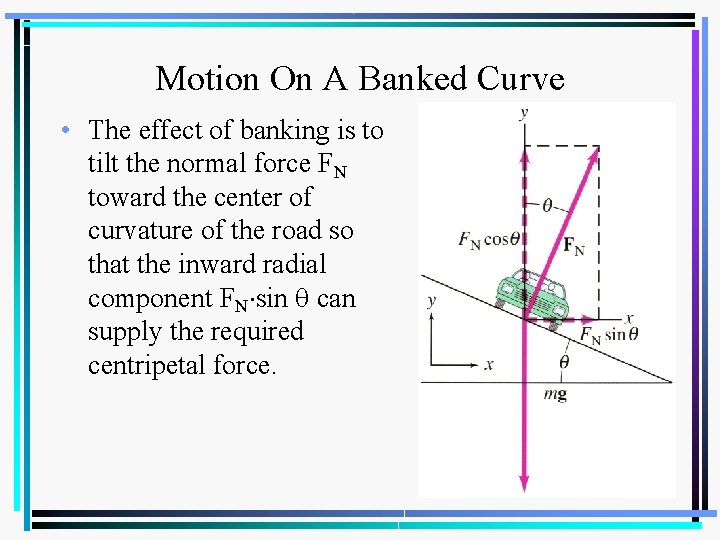
Motion On A Banked Curve • The effect of banking is to tilt the normal force Fn toward the center of curvature of the road so that the inward radial component FN sin can supply the required centripetal force. • Vehicles can make a sharp turn more safely if the road is banked. If the vehicle maintains the speed for which the curve is designed, no frictional force is needed to keep the vehicle on the road.

Motion On A Banked Curve • The effect of banking is to tilt the normal force FN toward the center of curvature of the road so that the inward radial component FN sin can supply the required centripetal force.

Motion On A Banked Curve • There is no acceleration along the y axis, so the sum of the forces in the y plane is zero: • The horizontal component of the normal force FN, the force the road exerts against the car, provides the necessary centripetal force. Because the only force in the x plane is the centripetal force:

Motion On A Banked Curve • This equation gives the banking angle that allows a car to travel in a curve of radius r with constant speed v and require no friction force. • Goldilocks: Just Right!

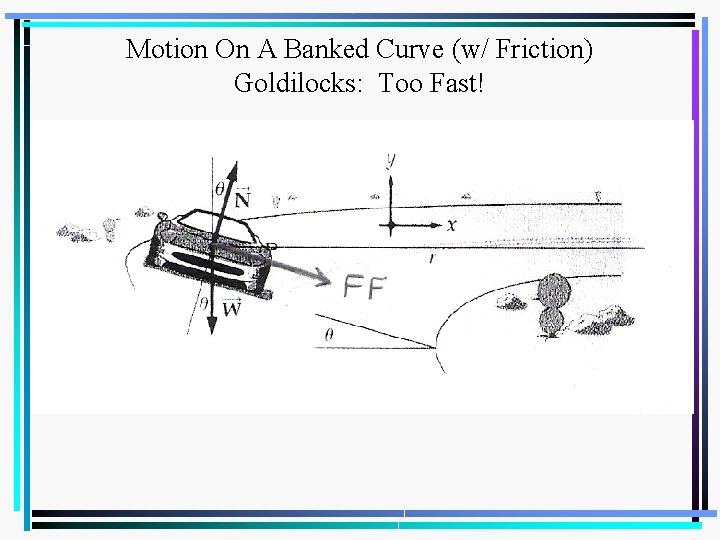
Motion On A Banked Curve • A banked curve is designed for one specific speed, called the “design speed”. – If the banked curve is icy so that there is no friction force at all, then traveling at a speed higher than the design speed means the car will slide out, up, and over the edge. – Traveling at a lower speed than the design speed means the car will slide in, down, and off the bank. • When a banked curve has to be negotiated at a speed above the design speed (or if you are asked to find the maximum speed), friction is required. The frictional force Ff acts parallel to the road surface.

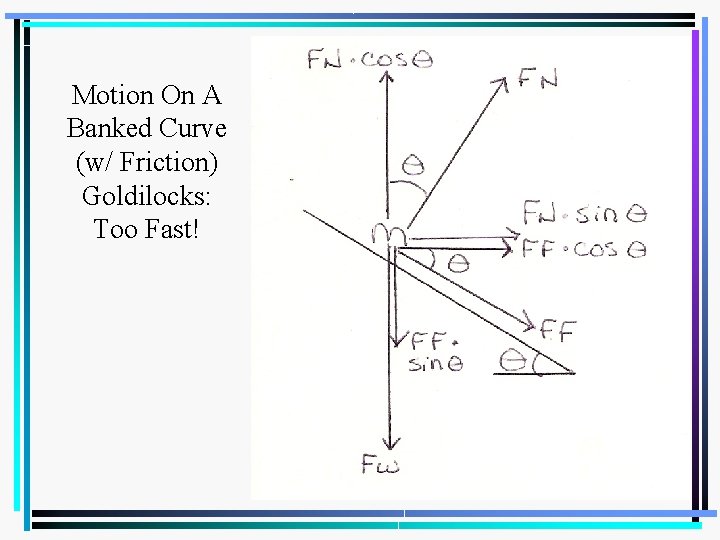
Motion On A Banked Curve (w/ Friction) Goldilocks: Too Fast!

Motion On A Banked Curve (w/ Friction) Goldilocks: Too Fast!

Motion On A Banked Curve (w/ Friction) • Resolve the normal force FN and friction FF into horizontal and vertical components. • The horizontal components of FN and FF are both directed inward toward the center of the curve, therefore, these two force components combine to determine the centripetal force; ΣFx = m·ac.

Motion On A Banked Curve (w/ Friction) • Because there are no unbalanced forces in the vertical direction, the upward forces must equal the downward forces, therefore: • Substitute into both equations.

Motion On A Banked Curve (w/ Friction) • Solve both equations for Fn and set these equations equal to each other (because FN = FN as there is only one force acting normal to the surface). From this equation, the unknown variable can be determined.

Motion On A Banked Curve (w/ Friction) • For problems involving a minimum speed for the vehicle to travel around the curve without skidding, the frictional force is directed up the incline to keep the vehicle from sliding down to the bottom of the banked curve. • Resolve the normal force FN and friction FF into horizontal and vertical components.

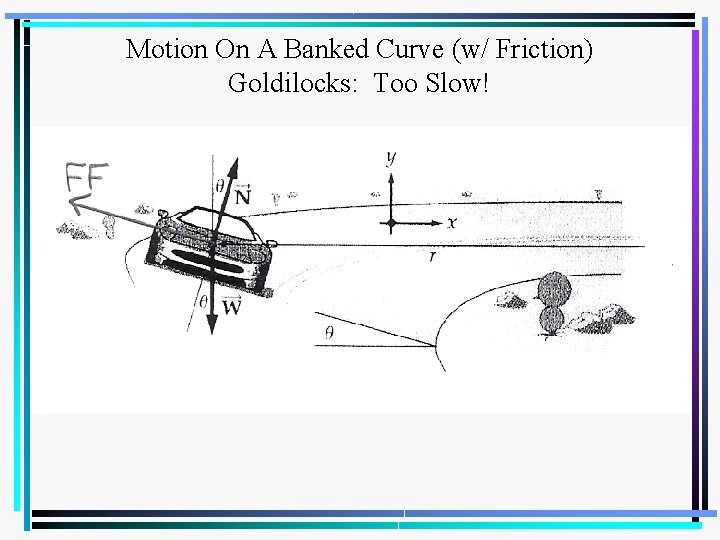
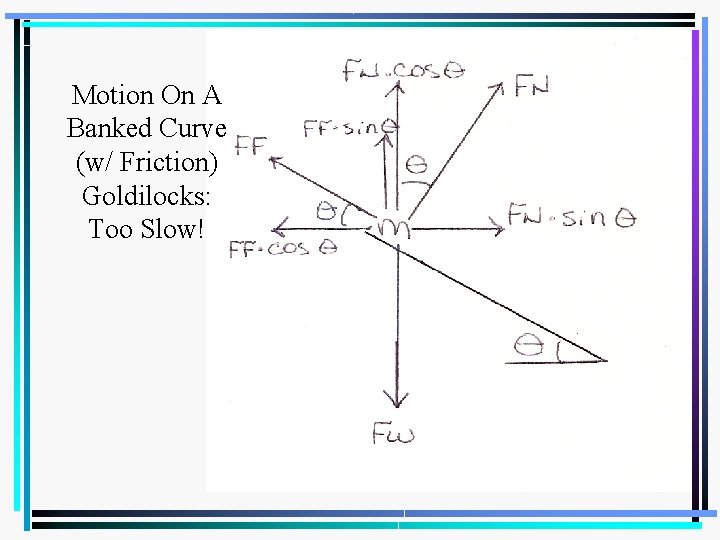
Motion On A Banked Curve (w/ Friction) Goldilocks: Too Slow!

Motion On A Banked Curve (w/ Friction) Goldilocks: Too Slow!

Motion On A Banked Curve (w/ Friction) • The horizontal component of FN is inward toward the center of the curve and is positive; FF is directed outward away from the center of the curve and is negative. These two force components combine to determine the centripetal force; ΣFx = m·ac.

• Because there are no unbalanced forces in the vertical direction, the upward forces must equal the downward forces, therefore: • Substitute into both equations.

• Solve both equations for Fn and set these equations equal to each other (because FN = FN as there is only one force acting normal to the surface). From this equation, the unknown variable can be determined.

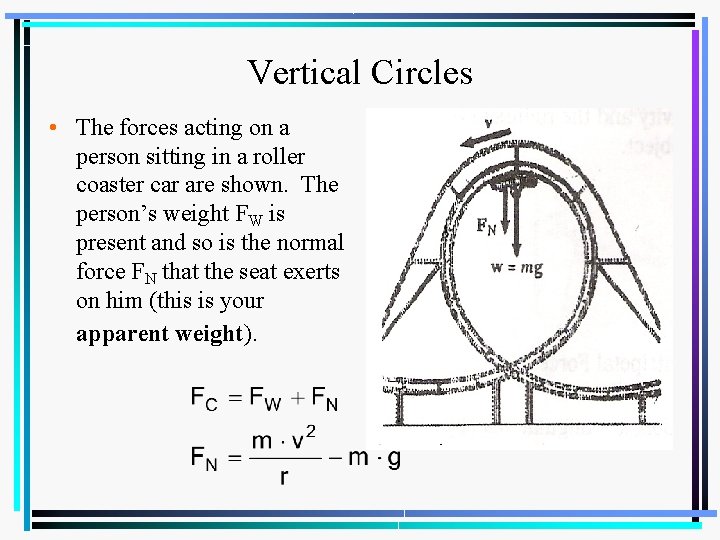
Vertical Circles • The force of gravity causes the speed of an object in a vertical circular path to vary. The object accelerates on the downward portion of its circular path and decelerates on the upward portion of the circular path. • At the top and bottom of a vertical circular path, the weight and the normal force (or an equivalent supporting force, such as tension) are the only forces acting on an object. The centripetal force is supplied by the resultant of the weight and a supporting force (often the normal force).

Vertical Circles • The forces acting on a person sitting in a roller coaster car are shown. The person’s weight FW is present and so is the normal force FN that the seat exerts on him (this is your apparent weight).

Vertical Circles • The normal force FN, the force you feel on the seat of your pants, can be positive, negative, or zero. • A negative value for FN means the passenger has to be strapped in, with the straps exerting an upward force. Such a situation would be dangerous, and roller coaster designers avoid this. • If FN = 0 N, the person seems to be weightless as well as upside down.

Vertical Circles • The forces on an airplane pilot at the bottom of a dive can be quite large. • Gravity pulls downward and the seat exerts its usual normal force FN, this time upward.

Vertical Circles • At the bottom of the dive, the normal force can only be positive, must be greater than the weight, and can become very large. A roller coaster at the bottom of the loop provides the same forces. • The acceleration can be expressed as: • This acceleration can be expressed in terms of g’s, where g’s are determined by dividing the centripetal acceleration by gravity. One g is 9. 8 m/s 2. The number of g’s represents the relative pull of gravity on the body that the person experiences.

Vertical Circles • Experiencing a significant number of g’s makes the work of the heart more difficult. Accelerations of eight to ten g’s make it difficult for the circulatory system to get enough blood to the brain and may result in blackouts. Pressure suits that squeeze on the legs push blood back into the rest of the body, including the brain, and help prevent blackouts.

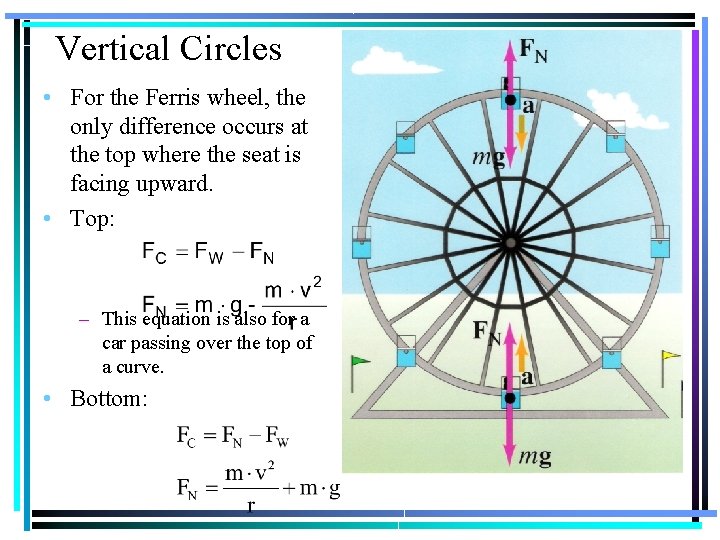
Vertical Circles • For the Ferris wheel, the only difference occurs at the top where the seat is facing upward. • Top: – This equation is also for a car passing over the top of a curve. • Bottom:

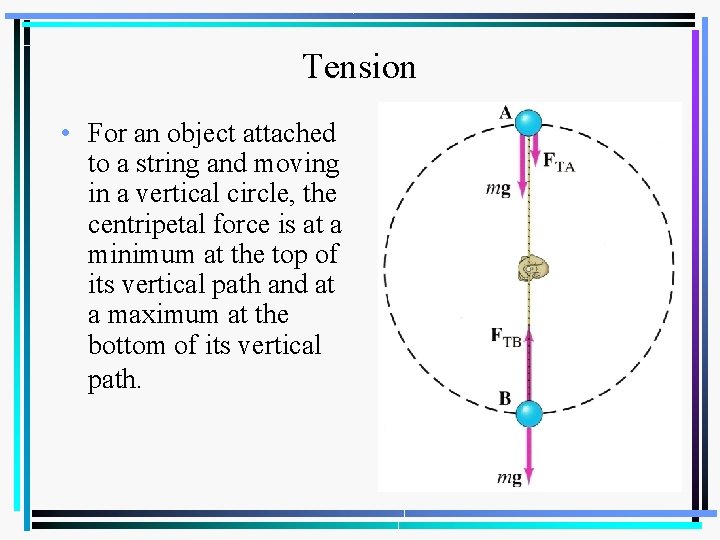
Tension • For an object attached to a string and moving in a vertical circle, the centripetal force is at a minimum at the top of its vertical path and at a maximum at the bottom of its vertical path.

Tension • Top: the centripetal force on the object equals the tension of the string plus the weight of the ball, both acting toward the center of the vertical circle. Mathematically: • Bottom: the centripetal force on the object is equal to the difference between the tension of the string and the weight of the object. The tension is exerted inward toward the center of the vertical circle, while the weight is directed away from the center of the vertical circle. Mathematically:

Critical Velocity (vmin) • Critical velocity: velocity below which an object moving in a vertical circle will not describe a circular path. • Critical velocity depends on the acceleration due to gravity and the radius of the vertical circle, not on the mass of the object.

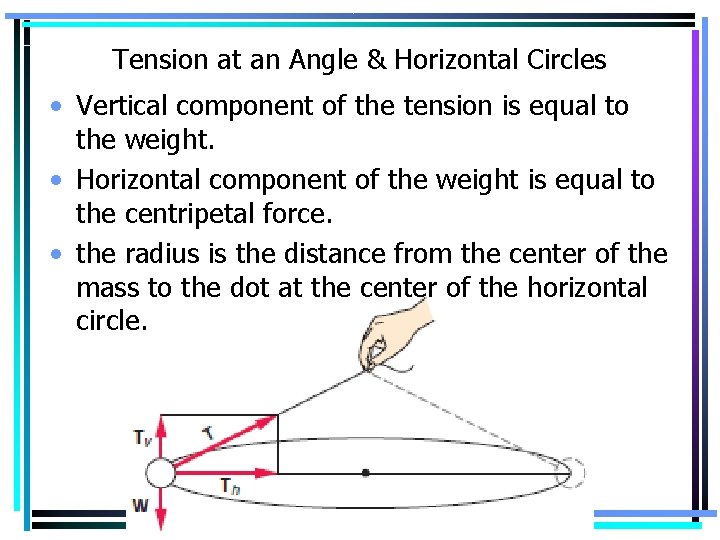
Tension at an Angle & Horizontal Circles • Vertical component of the tension is equal to the weight. • Horizontal component of the weight is equal to the centripetal force. • the radius is the distance from the center of the mass to the dot at the center of the horizontal circle.

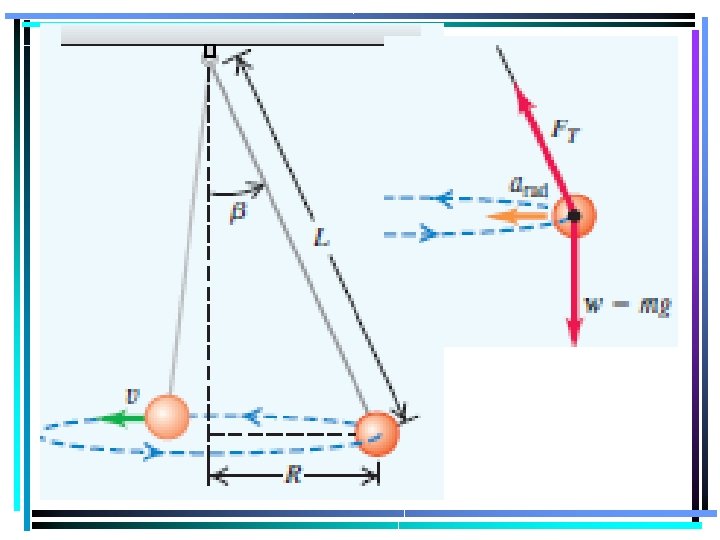
Conical Pendulum is L r T • For conical pendulums, centripetal force is provided by a component of the tension. • is the angle between the vertical and the cord. Fw = m·g


Conical Pendulum

Fn Difference? • In every previous inclined plane problem such as a skier on a hill or a block on a ramp, the normal force is given by Fn = m·g·cos . • In every banked curve problem the normal force is given by Fn=m·g/cos . • Both equations are correct! • The difference is due to the direction of the acceleration. – the direction of the acceleration in the inclined plane problem is down toward the bottom of the incline. There is no component of the acceleration in the normal direction.

– the direction of the acceleration in the banked curve is horizontally toward the center of the circle. This produces a component of acceleration in the normal direction. • In the inclined plane problems, I taught you to rotate the x- and y- axes so that the x-axis is parallel to the surface and the y-axis is perpendicular to the surface. We did not do this with the banked turn problems. – This results in the acceleration being zero on the y axis for both cases. – In the inclined plane problems, the acceleration is zero along the normal perpendicular to the incline; thus the normal force equals a component of gravity. )

– In the frictionless banked turn, the acceleration is zero vertically; thus the force of gravity equals a component of the normal force. – In the inclined plane problems, one component of gravity causes the acceleration (the other component cancels out the normal force). – In the banked turn, one component of the normal force causes the acceleration (the other component cancels out the force of gravity).

For Uniform Circular Motion: n = number of revolutions (rotations) r = radius t = time Period = time for one revolution (rotation)

Web Sites • Amusement Park Physics • Roller Coasters and Amusement Park Physics • Coaster. Quest. com