Warmup 129 Circular Motion LOOK Is it a





































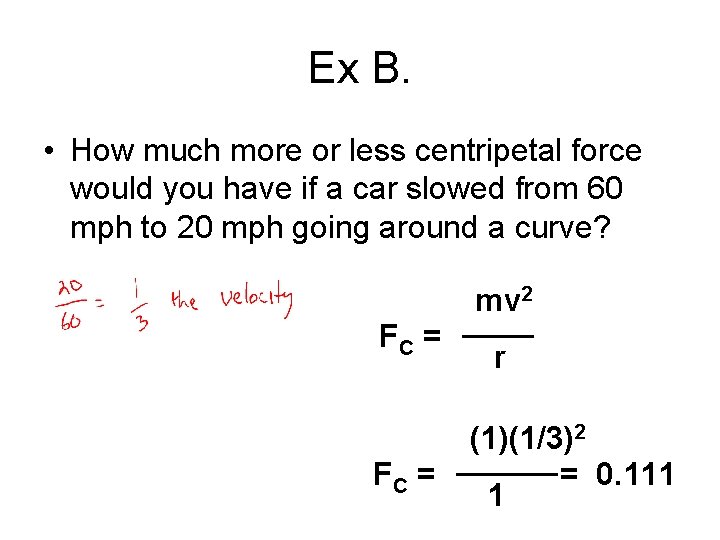



















- Slides: 70

Warm-up (12/9): Circular Motion LOOK! Is it a bird? Is it a plane? No! It’s Percy the Physics Pig!! =) *Do not touch planes / pigs / lab equipment (that includes string) 5 point deduction each time it occurs before lab - yes – I’m serious. 1. Take out “Give it a whirl” data table. 2. Dig out Plickers or pick up a new card. Not sure of your number – check the number next to your name on roster.

(12/9/15) Wednesday Agenda: • Warm-up / Review: plickers or traditional (with demo – 10 -15 min. ) • Address questions or concerns remaining from “Give it a whirl” lab or data discussion. ” (5 min. ) • Introduce “When Pigs Fly” Challenge. (Begin set-up and data collection 20 min. )

Plicker Alternative • What direction does centripetal force act in horizontal circular motion? • What direction does centripetal acceleration occur? • What created the centripetal force in the Give it a Whirl – stopper lab? • What will happen to a piece of cork floating in water if it is rotated in a circle? • What will happen to air bubble in a liquid if it is spun on the International Space Station?

Tasks: • Complete “Give it a whirl” activity and analysis • Conduct lab: Choose guided inquiry or design your own experiment • EXPERIENCE THE DERIVATION Time Management: set-up, collect data today – debrief and conduct analysis of data as a team tomorrow.

Think back to Newton’s Laws and Give it a Whirl lab • The net force is related to the acceleration of an object…and is stated in the following three equations:

• Circumference = 2*pi*Radius

Circular Motion Objectives this week: • Describe circular motion in terms of inertia and centripetal force. • Use lab data, to determine the relationships among mass, centripetal force, velocity and radius when motion is circular. • Apply equation for calculating centripetal force to every day situations.

When Pigs Fly Challenge • Describe circular motion in terms of centripetal acceleration and centripetal force. • Use lab data, to determine the relationships among velocity and angle of when motion is circular (Conical Pendulum). • Apply equation for calculating centripetal force to every day situations.

OSHA Safety Video • When battling the storm troopers, • what did the Ewok forget to do in this battle scene? • PIG LAB – Goggles for Murphy’s Law! =)

Ticket out the door 1. Use sticky note up front Name on one side question on other 2. List one thing you learned from Circular Motion lab 3. List a burning question about lab you still need answered. 4. Stick on the board on your way out of the door.

Circular Motion Terms • Axis- is the straight line around which rotation takes place. Two types of circular motion • Rotation- also called spin; when an object turns around an internal axis. • Revolution- When an object turns around an external axis Rotating around an Axis

Demo 1: Have you ever swung a pail of water over your head?

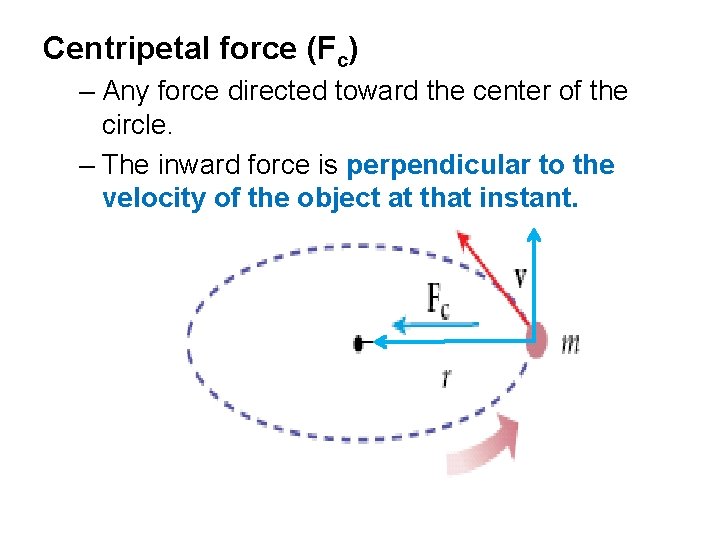
Centripetal force (Fc) – Any force directed toward the center of the circle. – The inward force is perpendicular to the velocity of the object at that instant.

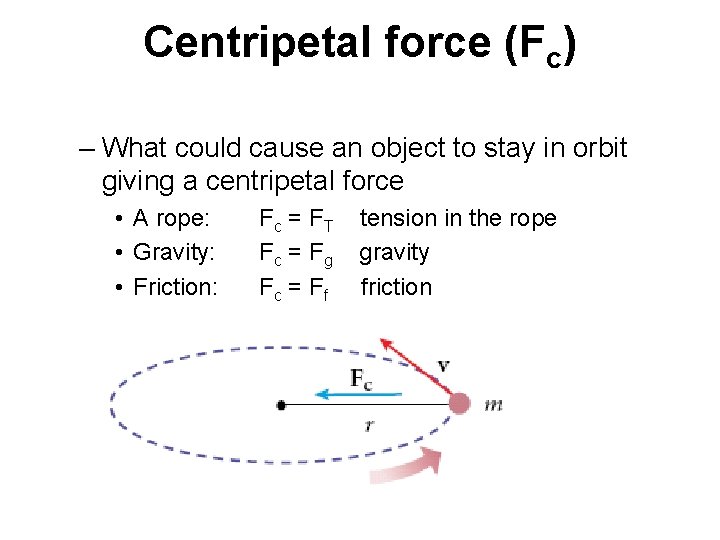
Centripetal force (Fc) – What could cause an object to stay in orbit giving a centripetal force • A rope: • Gravity: • Friction: Fc = F T Fc = F g Fc = F f tension in the rope gravity friction

Demo 2: The Horizontal vs. Vertical Twirl… Give it a Whirl ! What direction is the force of the string pulling?

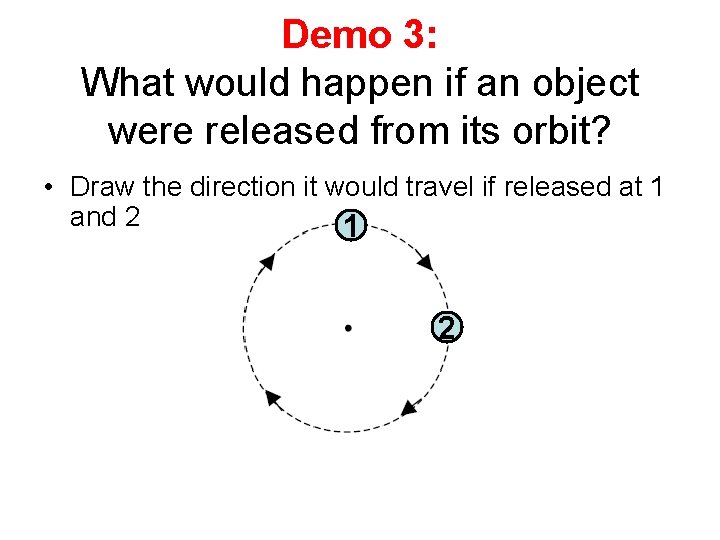
Demo 3: What would happen if an object were released from its orbit? • Draw the direction it would travel if released at 1 and 2 1 2

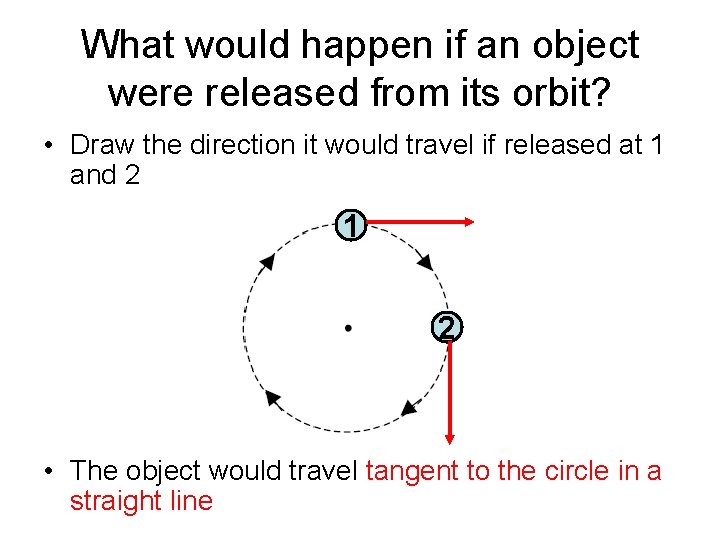
What would happen if an object were released from its orbit? • Draw the direction it would travel if released at 1 and 2 1 2 • The object would travel tangent to the circle in a straight line

Linear/Tangential Velocity • Objects moving in a circle still have a linear velocity = distance/time. • This is often called tangential velocity, since the direction of the linear velocity is tangent to the circle. v

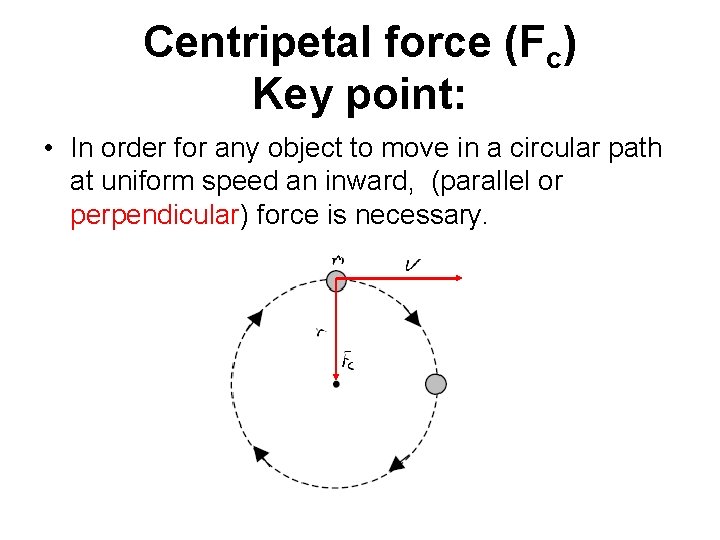
Centripetal force (Fc) Key point: • In order for any object to move in a circular path at uniform speed an inward, (parallel or perpendicular) force is necessary.

Centripetal force (Fc) Recap • The ball’s speed may or may not be constant – however its direction and velocity are constantly changing. • Thus, the object is constantly accelerating. • In order for an object to be accelerated a force must act upon it- according to Newton’s second law.

Centripetal force (Fc) Recap: • As the ball moves around – the rope is exerting an (inward or outward) centripetal force on the ball. • Force of the rope on the ball is (perpendicular or parallel) to the ball’s direction of travel at that instant.

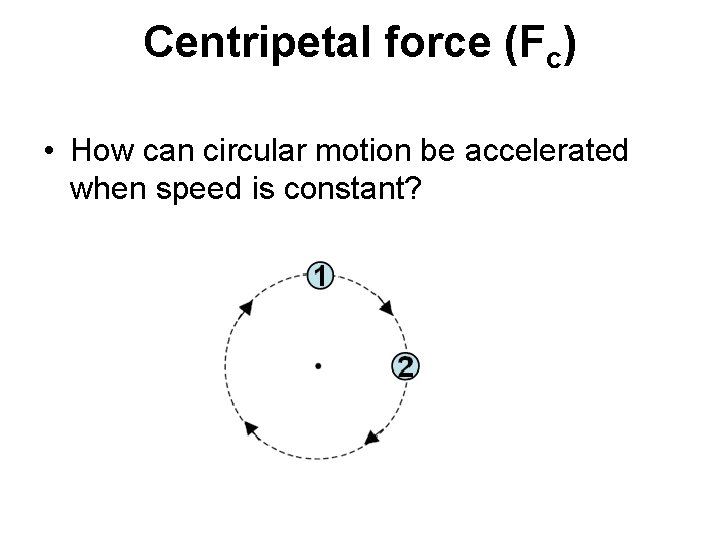
Centripetal force (Fc) • How can circular motion be accelerated when speed is constant?

Centripetal force (Fc) • Velocity has BOTH speed and direction. • In circular motion – – Direction is always changing. – So, velocity is ALWAYS changing. • According to Newton’s 2 nd law • F = ma • Acceleration requires a net force.

Your Turn • When a car turns to the left, why do passengers slide to the right? • When your friend slams on the breaks and you feel a ‘force’ push you forward – what causes this sensation?

Inertia • Newton’s 1 st law • Once an object is in motion – it stays in motion until acted upon by an outside, unbalanced force.

# 1 Misconception • Inertia is often mistaken for the ‘feeling of a force. ’ • Commonly referred to as centri. Fugal force. • According to physicist, this is a fictitious or false force.

When a car turns to the left, why do passengers slide to the right? What provides the inward Centripetal force?

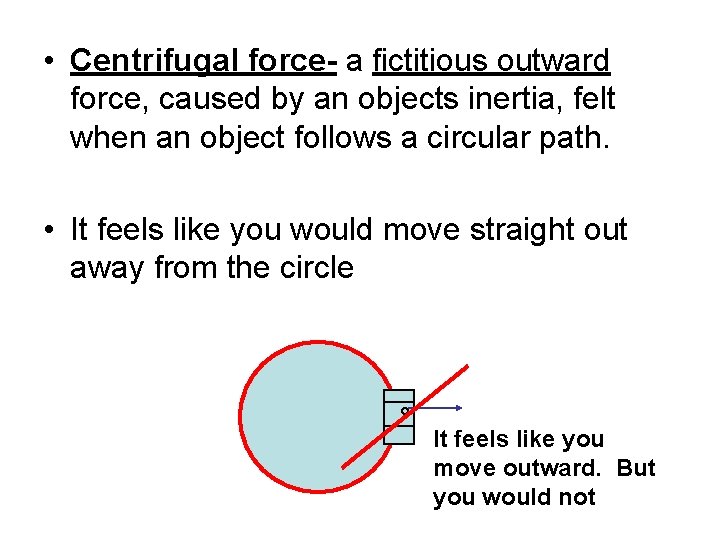
• Centrifugal force- a fictitious outward force, caused by an objects inertia, felt when an object follows a circular path. • It feels like you would move straight out away from the circle It feels like you move outward. But you would not

• An objects inertia would take it directly ahead tangent to the circle

What provides the centripetal force in your washing machine?

Centripetal Force • Helpful hint: • When doing Newton’s 2 nd Law of motion equations – think of the Fc as the net force. F = ma c • All the forces acting onca rotating object will add up to equal mass times the centripetal acceleration.

Think back to Newton’s Laws • The net force is related to the acceleration of an object…and is stated in the following three equations:

• Circumference = 2*pi*Radius


Warm-up: • What is the difference between centripetal and centrifugal force? Explain with an example. • What is the relationship between centripetal force and velocity? • What is the relationship between centripetal force mass?

“Give it a Whirl” Centrifugal force - stopper lab

“Give it a Whirl” • What 4 factors could affect circular motion of the stopper? - Velocity - Mass - Centripetal force - Radius

Useful equations for Centripetal force (Fc) lab Fc = mac V= V= T= d t 2πr T 1 T= period (s) seconds per rotation f f= frequency (hz) rotations per second

Calculating the period (T) T = time it takes for 20 revolutions number of revolutions (20)

State three relationships you discovered during the lab.

Let’s use these to derive the formula for centripetal force.

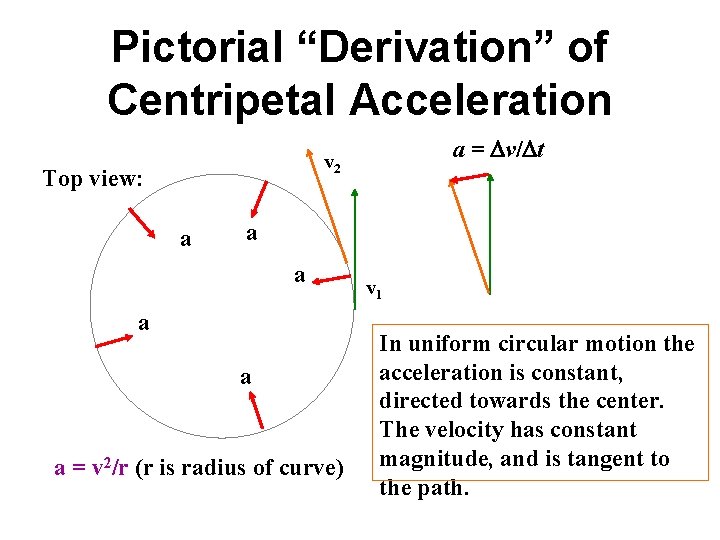
Pictorial “Derivation” of Centripetal Acceleration a = Dv/Dt v 2 Top view: a a a = v 2/r (r is radius of curve) v 1 In uniform circular motion the acceleration is constant, directed towards the center. The velocity has constant magnitude, and is tangent to the path.

Speed/Velocity in a Circle Consider an object moving in a circle around a specific origin. The DISTANCE the object covers in ONE REVOLUTION is called the CIRCUMFERENCE. The TIME that it takes to cover this distance is called the PERIOD. Speed is the MAGNITUDE of the velocity. And while the speed may be constant, the VELOCITY is NOT. Since velocity is a vector with BOTH magnitude AND direction, we see that the direction o the velocity is ALWAYS changing. We call this velocity, TANGENTIAL velocity as its direction is draw TANGENT to the circle.

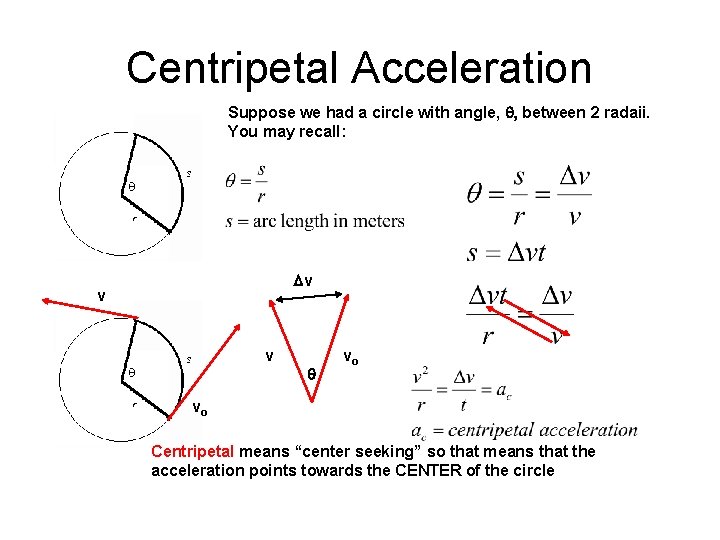
Centripetal Acceleration Suppose we had a circle with angle, q, between 2 radaii. You may recall: Dv v v q vo vo Centripetal means “center seeking” so that means that the acceleration points towards the CENTER of the circle

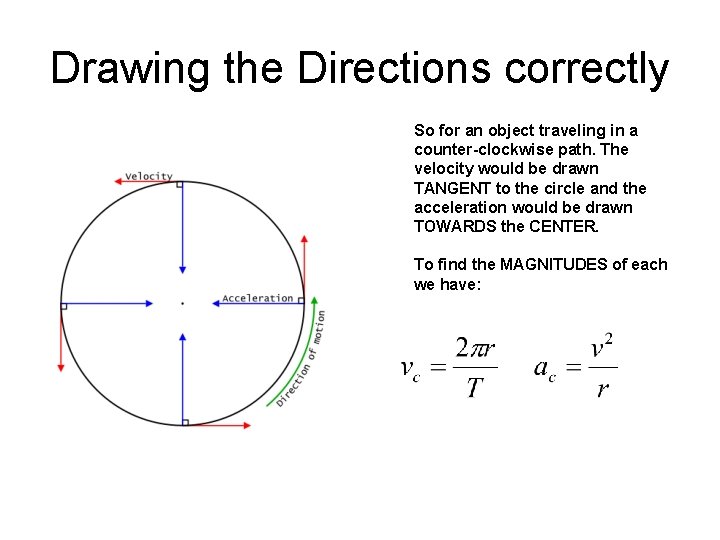
Drawing the Directions correctly So for an object traveling in a counter-clockwise path. The velocity would be drawn TANGENT to the circle and the acceleration would be drawn TOWARDS the CENTER. To find the MAGNITUDES of each we have:

Circular Motion and N. S. L Recall that according to Newton’s Second Law, the acceleration is directly proportional to the Force. If this is true: Since the acceleration and the force are directly related, the force must ALSO point towards the center. This is called CENTRIPETAL FORCE. NOTE: The centripetal force is a NET FORCE. It could be represented by one or more forces. So NEVER draw it in an F. B. D.

Tuesday (1/20) • Take out your ws “ Equations for circular motion”. Has equation bank at top. • Complete Problem Set #1 I will finish getting recommendations this period for next year – if you did not give it to me on Friday.

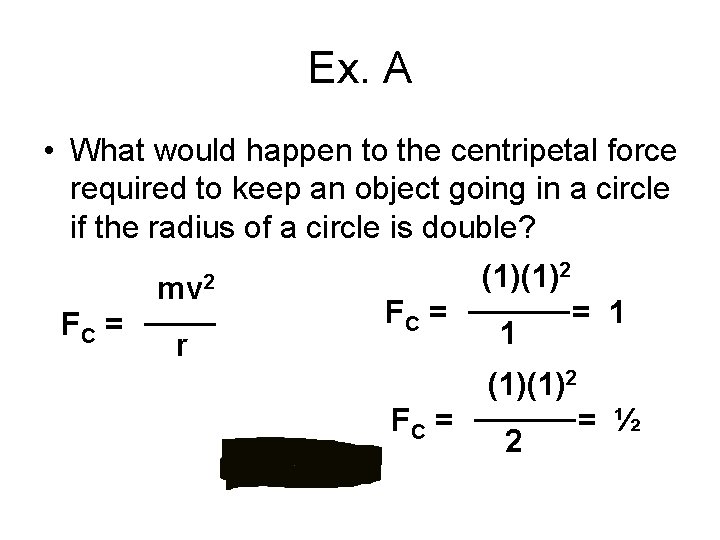
Ex. A • What would happen to the centripetal force required to keep an object going in a circle if the radius of a circle is double?

Ex. A • What would happen to the centripetal force required to keep an object going in a circle if the radius of a circle is double? mv 2 FC = r (1)(1)2 FC = 1 (1)(1)2 FC = 2 = ½

Ex. B • How much more or less centripetal force would you have if a car slowed from 60 mph to 20 mph going around a curve? – Start by figuring out how much of your initial velocity you are going
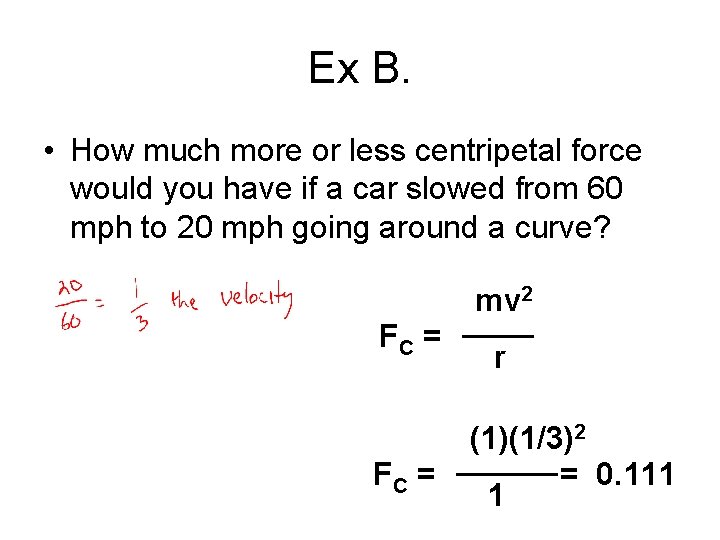
Ex B. • How much more or less centripetal force would you have if a car slowed from 60 mph to 20 mph going around a curve? mv 2 FC = r (1)(1/3)2 = 0. 111 1

Ex. C • Kent spins in his chair with a frequency of 0. 5 Hz. What is the period of his spin? • Hint: you will need to go back to notes to find the equation for period.

Ex. C • Kent spins in his chair with a frequency of 0. 5 Hz. What is the period of his spin?

Ex. D • A record takes 1. 3 s to make one complete rotation. An object on this record is 0. 12 m from the center. What is its velocity?

Ex. D • A record takes 1. 3 s to make one complete rotation. An object on this record is 0. 12 m from the center. What is its linear velocity?

Ex. E • The pilot of a 60, 500 kg jet plane is flying in circles whose radius is 5. 00 x 104 m. It takes 1. 8 x 103 s to make one rotation. a. What is the velocity of the plane? b. What would be the centripetal force?

Ex. E • The pilot of a 60, 500 kg jet plane is flying in circles whose radius is 5. 00 x 104 m. It takes 1. 8 x 103 s to make one rotation. a. What is the velocity of the plane? b. What would be the centripetal force?

Ex. F • What is the centripetal acceleration of an bike traveling a tangential speed of 8 meters per second in a circle that has a radius of 5 meters?

Ex. F • What is the centripetal acceleration of an bike traveling a tangential speed of 8 meters per second in a circle that has a radius of 5 meters?

Problem Set 1 What will happen to the centripetal force required to keep an object going in a circle if: 1. The mass of the object is doubled and the radius of the circle is cut in half 2. Mass, radius, and velocity are all doubled

Problem Set 1 What will happen to the centripetal force required to keep an object going in a circle if: 1. The mass of the object is doubled and the radius of the circle is cut in half

Problem Set 1 What will happen to the centripetal force required to keep an object going in a circle if: 2. Mass, radius, and velocity are all doubled

Problem Set 1 3. A of a 50 kg girl is bicycling in circles with a radius of 5. 00 m. It takes 12 s to make one rotation. a. What is the velocity of the girl? b. What would be the centripetal force?

Problem Set 1 3. A of a 50 kg girl is bicycling in circles with a radius of 5. 00 m. It takes 12 s to make one rotation. a. What is the velocity of the girl? b. What would be the centripetal force?

Problem Set 1 3. A of a 50 kg girl is bicycling in circles with a radius of 5. 00 m. It takes 12 s to make one rotation. a. What is the velocity of the girl? b. What would be the centripetal force?

Thought to ponder and recap: • If you were to put a bubble in a bag of water on the international space station and spin in in a circle…which way would the bubble travel? (inward, outward, stay random throughout liquid) Explain your reasoning Let’s find out! PLICKERS!

Friday Warm-up: Circular Motion 1. Take out “Flying pig / plane Lab” Use this time to compare data and complete post lab analysis. Paper clip your lab group together – make sure the # of your pig or plane is on front of all papers. Turn in to top tray.

Uniform Circular Motion Answers • 1. 2. 3. 4. 5. ac = 3. 09 m/s 2 agent exerting force = friction. 32 Newtons Min. coefficient = 0. 88 8. 1 km The force toward center of tub. The walls of drum exert the normal force (centripetal force)

Circular Motion Answers continued… 6) 18 m/s

Tue. Agenda • • Review any questions from lab Review questions from ws#1 Horizontal vs Vertical circular motion Practice Webassign #12 Review for quiz Re-read 109 -111 Lab Thur. will deal with page 112