Radial Acceleration Radial Centripetal Acceleration An object moving

Radial Acceleration

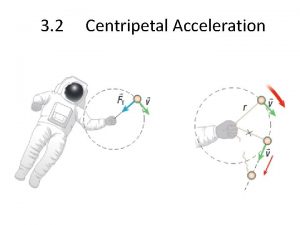
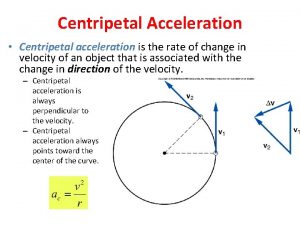
Radial (Centripetal) Acceleration An object moving in a circle at constant speed is always accelerating, since its direction is always changing. This acceleration acts towards the centre of the circle. As it is accelerating there must be an unbalanced force acting to change the direction. This force also acts towards the centre of the circle.
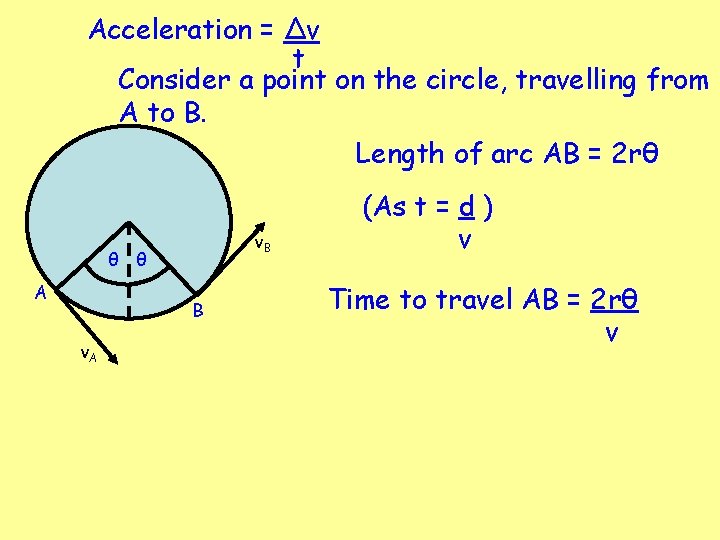
Acceleration = Δv t Consider a point on the circle, travelling from A to B. Length of arc AB = 2 rθ v. B θ θ A B v. A (As t = d ) v Time to travel AB = 2 rθ v
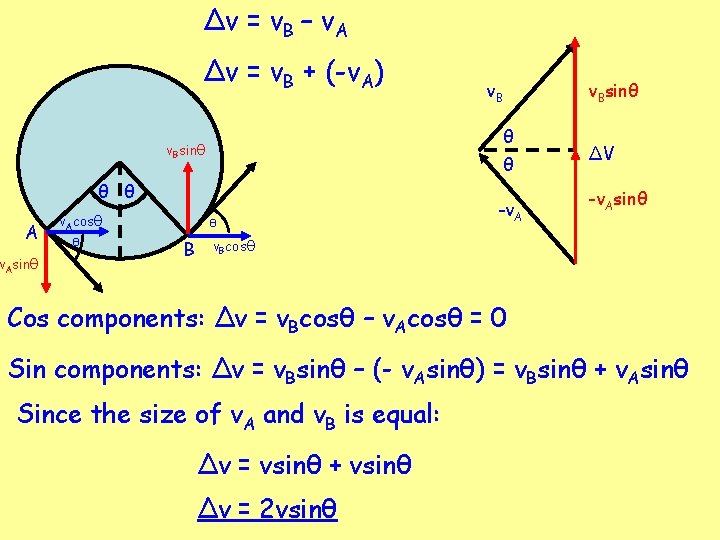
Δv = v. B – v. A Δv = v. B + (-v. A) θ θ θ v. Asinθ v. Acosθ θ θ B v. Bsinθ θ v. Bsinθ A v. B -v. A ΔV -v. Asinθ v. Bcosθ Cos components: Δv = v. Bcosθ – v. Acosθ = 0 Sin components: Δv = v. Bsinθ – (- v. Asinθ) = v. Bsinθ + v. Asinθ Since the size of v. A and v. B is equal: Δv = vsinθ + vsinθ Δv = 2 vsinθ

As: acceleration = Δv t a = 2 vsinθ 2 rθ v a = 2 v 2 sinθ (2 rθ) a = v 2 sinθ r θ As t 0, θ 0. As θ 0, sinθ 1 θ Radial Acceleration a r = v 2 r
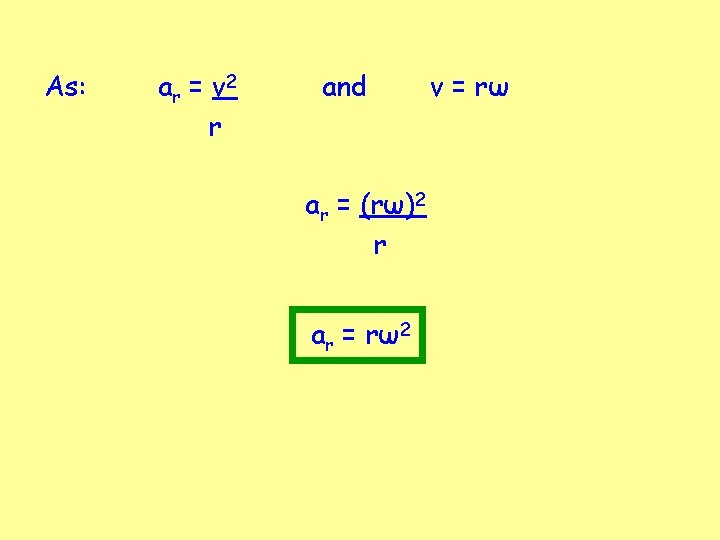
As: a r = v 2 r and ar = (rω)2 r ar = rω2 v = rω

The direction of this acceleration is always towards the centre of the circle, Centripetal, or radial acceleration, and is perpendicular to the velocity. This acceleration is provided by a centripetal or central force. All objects moving in a circular path experience a central force: e. g. Planetary Motion, electrons ‘orbiting’ nuclei and charged particles moving at right angles to a uniform magnetic field.
- Slides: 7