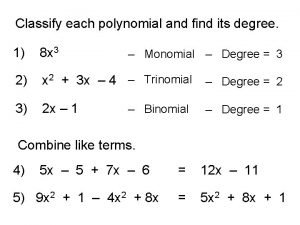4 2 Classifying Triangles Warm Up Classify each





















- Slides: 37

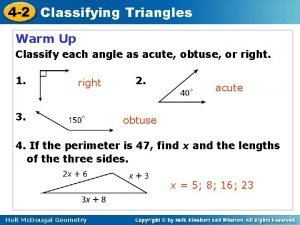
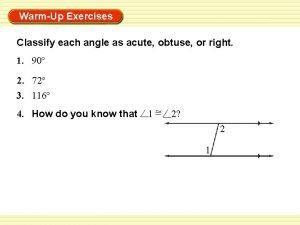
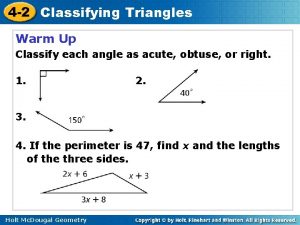
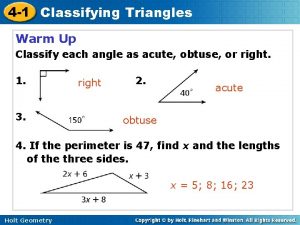
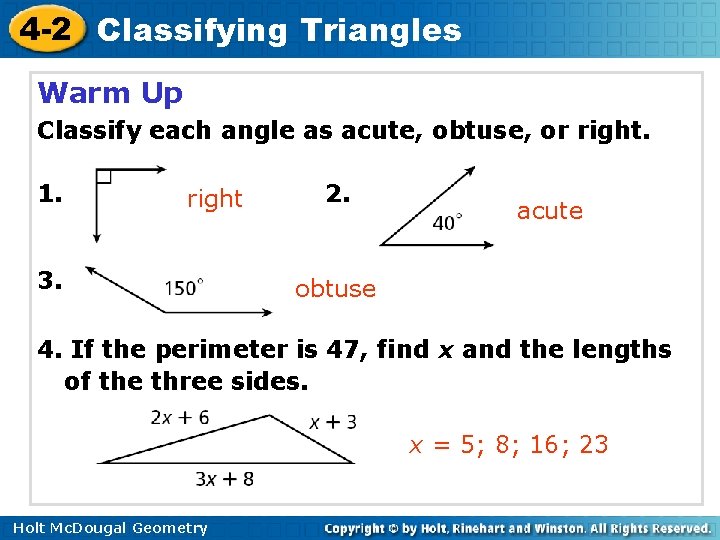
4 -2 Classifying Triangles Warm Up Classify each angle as acute, obtuse, or right. 1. right 3. 2. acute obtuse 4. If the perimeter is 47, find x and the lengths of the three sides. x = 5; 8; 16; 23 Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Recall that a triangle ( ) is a polygon with three sides. Triangles can be classified in two ways: by their angle measures or by their side lengths. Holt Mc. Dougal Geometry

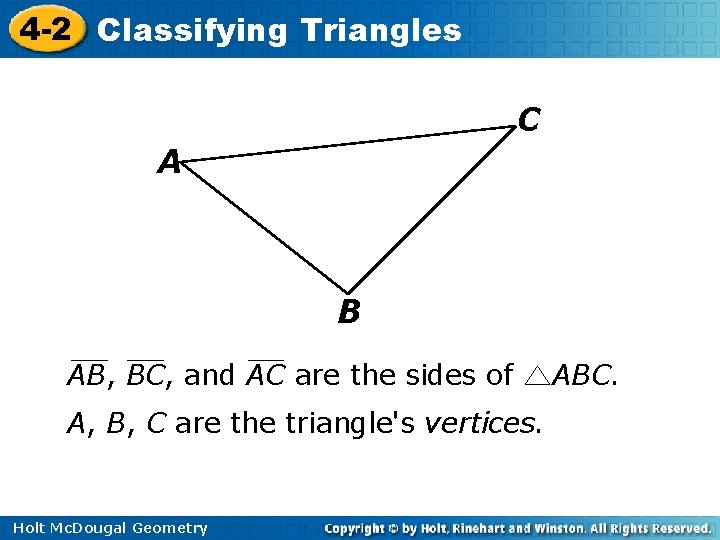
4 -2 Classifying Triangles C A B AB, BC, and AC are the sides of A, B, C are the triangle's vertices. Holt Mc. Dougal Geometry ABC.

*The angle formed by the three angles is a straight angle. 2. Make a conjecture about the sum of the measures of the angles of a triangle *The sum of the measures of the angles of a triangle is 180.

4 -2 Classifying Triangles Holt Mc. Dougal Geometry

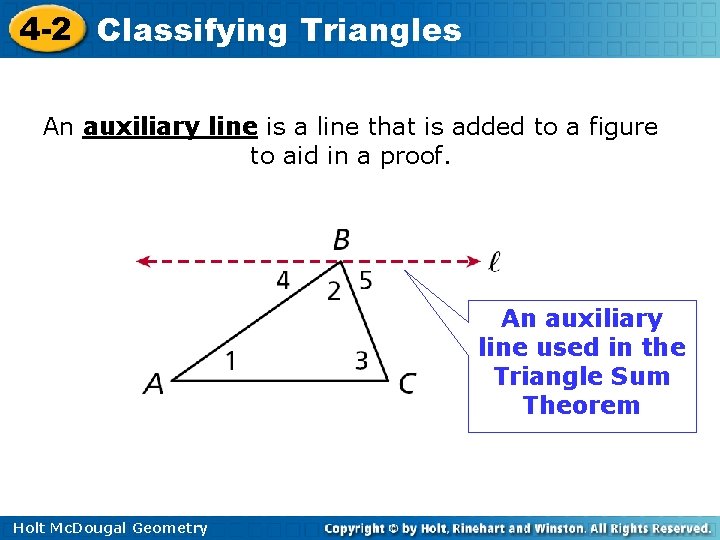
4 -2 Classifying Triangles An auxiliary line is a line that is added to a figure to aid in a proof. An auxiliary line used in the Triangle Sum Theorem Holt Mc. Dougal Geometry

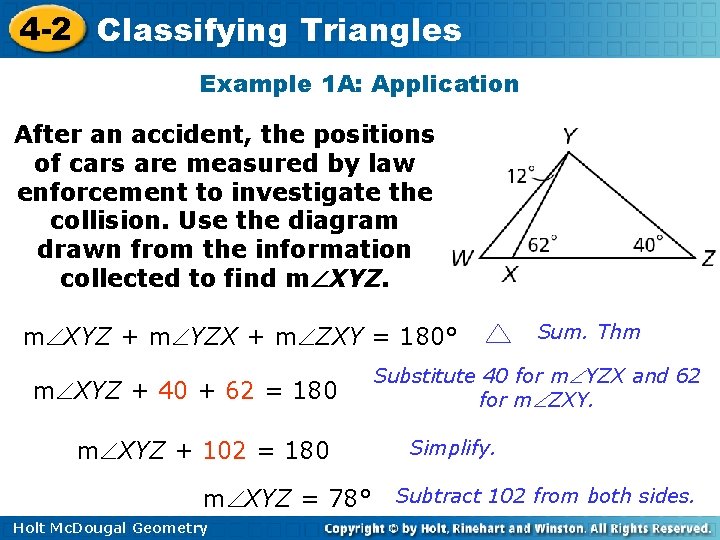
4 -2 Classifying Triangles Example 1 A: Application After an accident, the positions of cars are measured by law enforcement to investigate the collision. Use the diagram drawn from the information collected to find m XYZ + m YZX + m ZXY = 180° m XYZ + 40 + 62 = 180 m XYZ + 102 = 180 Sum. Thm Substitute 40 for m YZX and 62 for m ZXY. Simplify. m XYZ = 78° Subtract 102 from both sides. Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Proof Triangle Sum Theorem Prove: m 1 +m 2 + m 3 = 180 Holt Mc. Dougal Geometry

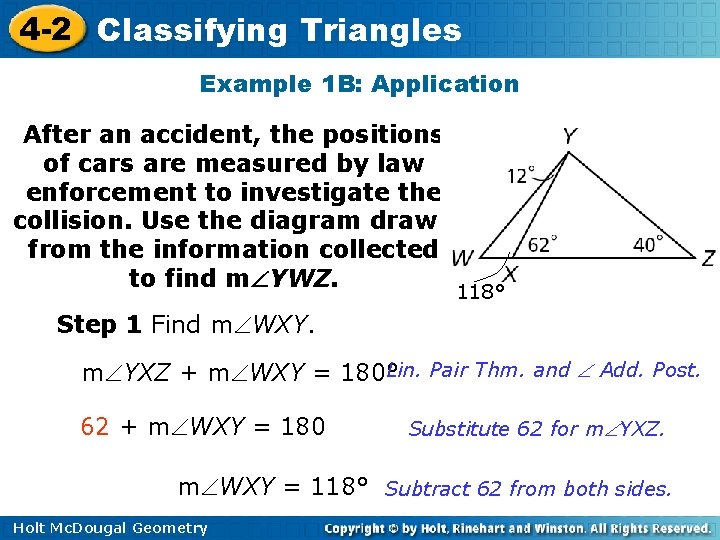
4 -2 Classifying Triangles Example 1 B: Application After an accident, the positions of cars are measured by law enforcement to investigate the collision. Use the diagram drawn from the information collected to find m YWZ. 118° Step 1 Find m WXY. Lin. Pair Thm. and Add. Post. m YXZ + m WXY = 180° 62 + m WXY = 180 Substitute 62 for m YXZ. m WXY = 118° Subtract 62 from both sides. Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Example 1 B: Application Continued After an accident, the positions of cars are measured by law enforcement to investigate the collision. Use the diagram drawn from the information collected to find m YWZ. 118° Step 2 Find m YWZ. m YWX + m WXY + m XYW = 180° Sum. Thm m YWX + 118 + 12 = 180 Substitute 118 for m WXY and 12 for m XYW. m YWX + 130 = 180 Simplify. m YWX = 50° Subtract 130 from both sides. Holt Mc. Dougal Geometry

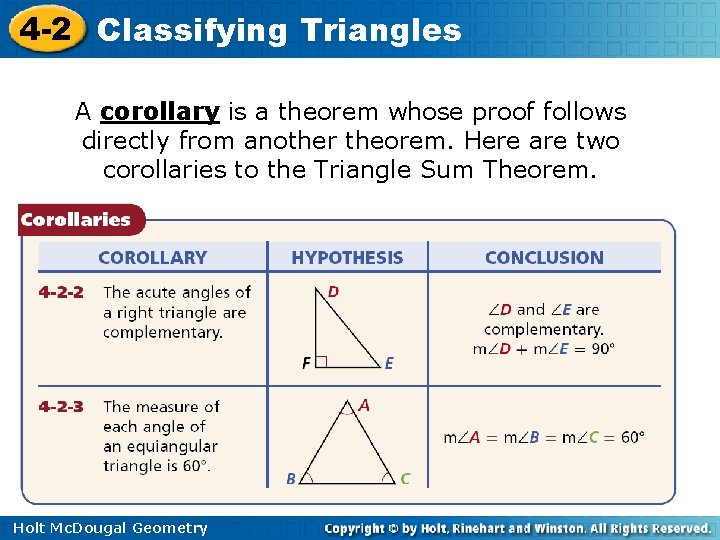
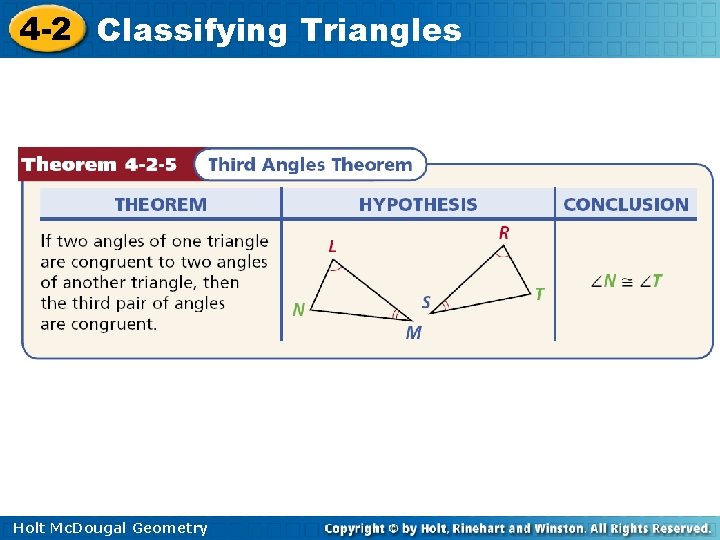
4 -2 Classifying Triangles A corollary is a theorem whose proof follows directly from another theorem. Here are two corollaries to the Triangle Sum Theorem. Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Holt Mc. Dougal Geometry

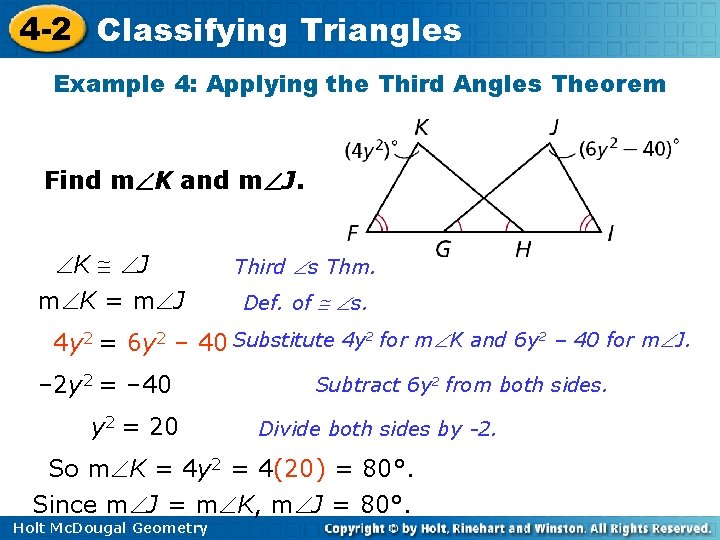
4 -2 Classifying Triangles Example 4: Applying the Third Angles Theorem Find m K and m J. K J m K = m J Third s Thm. Def. of s. 4 y 2 = 6 y 2 – 40 Substitute 4 y 2 for m K and 6 y 2 – 40 for m J. – 2 y 2 = – 40 y 2 = 20 Subtract 6 y 2 from both sides. Divide both sides by -2. So m K = 4 y 2 = 4(20) = 80°. Since m J = m K, m J = 80°. Holt Mc. Dougal Geometry

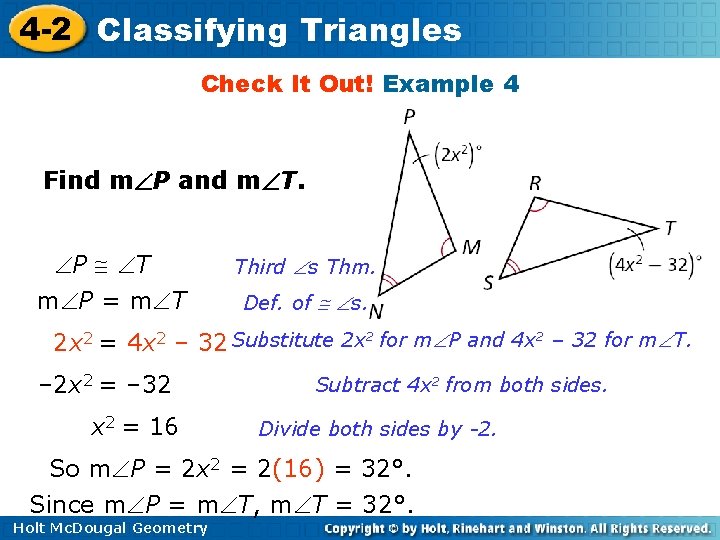
4 -2 Classifying Triangles Check It Out! Example 4 Find m P and m T. P T m P = m T Third s Thm. Def. of s. 2 x 2 = 4 x 2 – 32 Substitute 2 x 2 for m P and 4 x 2 – 32 for m T. – 2 x 2 = – 32 x 2 = 16 Subtract 4 x 2 from both sides. Divide both sides by -2. So m P = 2 x 2 = 2(16) = 32°. Since m P = m T, m T = 32°. Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Congruent Triangles Congruence Triangle by Side Angle Side (SAS) Side(SSS) Angle Side Angle (ASA) Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Objectives Apply SSS, ASA, and SAS to construct triangles and solve problems. Prove triangles congruent by using SSS, ASA, and SAS. Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Congruent Figures • Congruent Polygons – Have matching/congruent angles and sides • Name congruent polygons by listing corresponding vertices in the same order Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Triangle Congruence • Side-Side Postulate • Side-Angle-Side Postulate • Angle-Side-Angle Postulate • Angle-Side Theorem • Hypotenuse-Leg Theorem • CPCTC Holt Mc. Dougal Geometry

4 -2 Classifying Triangles INVESTIGATIONS: Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Side-Side Postulate • Referred to as SSS • If the three sides of one triangle are congruent to the three sides of another triangle, then the two triangles are congruent Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Remember! Adjacent triangles share a side, so you can apply the Reflexive Property to get a pair of congruent parts. Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Example 1: Using SSS to Prove Triangle Congruence Use SSS to explain why ∆ABC ∆DBC. It is given that AC DC and that AB DB. By the Reflexive Property of Congruence, BC BC. Therefore ∆ABC ∆DBC by SSS. Holt Mc. Dougal Geometry

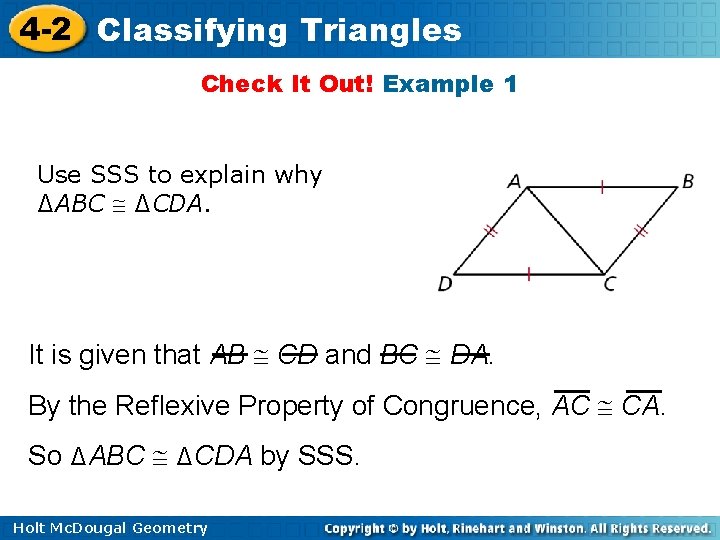
4 -2 Classifying Triangles Check It Out! Example 1 Use SSS to explain why ∆ABC ∆CDA. It is given that AB CD and BC DA. By the Reflexive Property of Congruence, AC CA. So ∆ABC ∆CDA by SSS. Holt Mc. Dougal Geometry

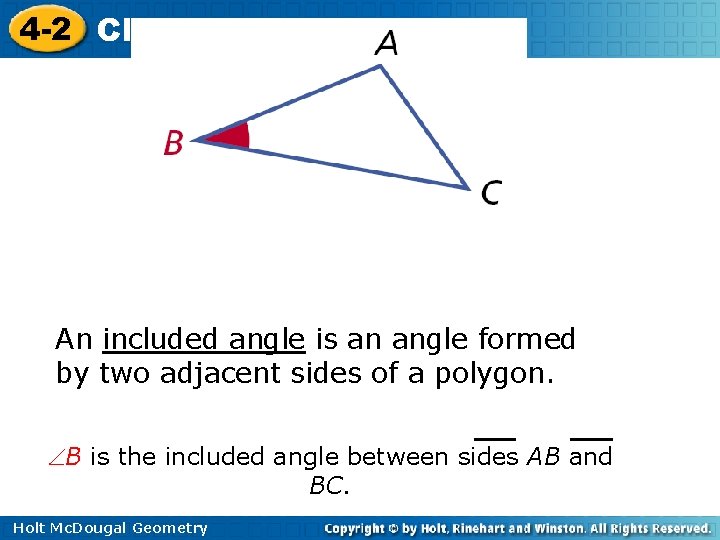
4 -2 Classifying Triangles An included angle is an angle formed by two adjacent sides of a polygon. B is the included angle between sides AB and BC. Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Side-Angle-Side Postulate • Referred to as SAS • If two sides and the included angle of one triangle are congruent to two Q sides and the E angle of another included P D Holt Mc. Dougal Geometry F R

4 -2 Classifying Triangles Check It Out! Example 2 Use SAS to explain why ∆ABC ∆DBC. It is given that BA BD and ABC DBC. By the Reflexive Property of , BC BC. So ∆ABC ∆DBC by SAS. Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Example 3 A: Verifying Triangle Congruence Show that the triangles are congruent for the given value of the variable. ∆MNO ∆PQR, when x = 5. PQ = x + 2 =5+2=7 QR = x = 5 PQ MN, QR NO, PR MO ∆MNO ∆PQR by SSS. Holt Mc. Dougal Geometry PR = 3 x – 9 = 3(5) – 9 = 6

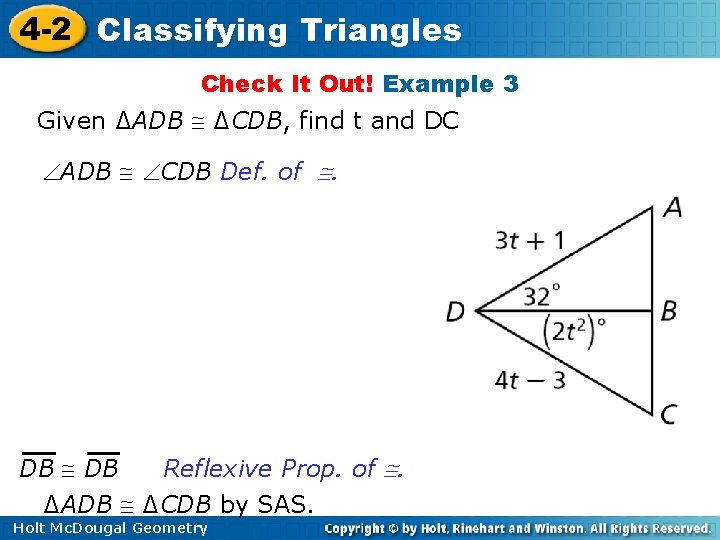
4 -2 Classifying Triangles Check It Out! Example 3 Given ∆ADB ∆CDB, find t and DC ADB CDB Def. of . DB Reflexive Prop. of . ∆ADB ∆CDB by SAS. Holt Mc. Dougal Geometry

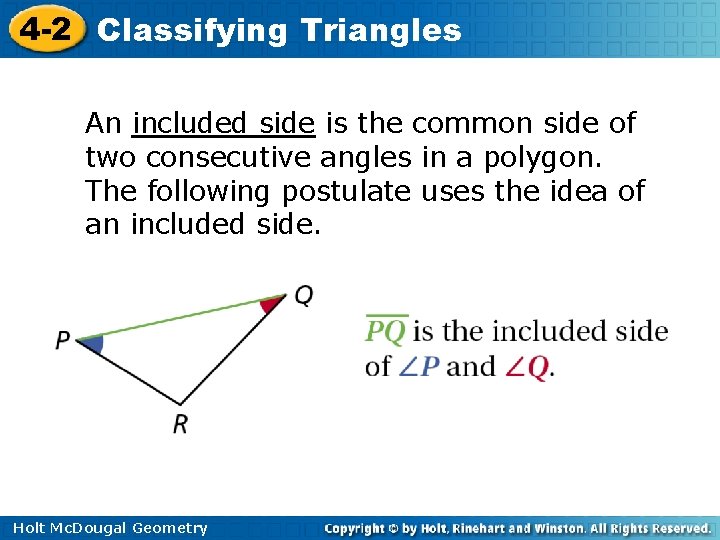
4 -2 Classifying Triangles An included side is the common side of two consecutive angles in a polygon. The following postulate uses the idea of an included side. Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Angle-Side-Angle Postulate • Referred to as ASA • If two angles and the included side of one triangle are congruent to two angles and the R M the included side of another triangle, then two triangles are congruent. T Holt Mc. Dougal Geometry S O N

4 -2 Classifying Triangles Example: Applying ASA Congruence Determine if you can use ASA to prove the triangles congruent. Explain. Two congruent angle pairs are give, but the included sides are not given as congruent. Therefore ASA cannot be used to prove the triangles congruent. Holt Mc. Dougal Geometry

4 -2 Classifying Triangles Angle-Side (AAS) Theorem • Referred to as AAS • If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the triangles are congruent. Holt Mc. Dougal Geometry

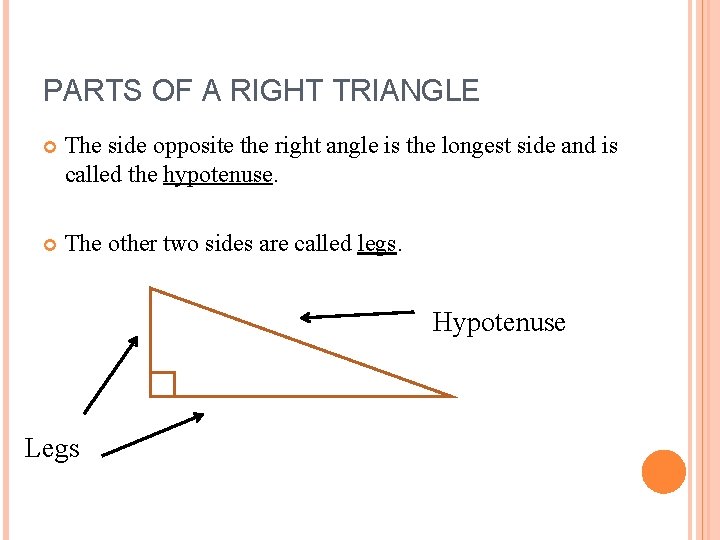
PARTS OF A RIGHT TRIANGLE The side opposite the right angle is the longest side and is called the hypotenuse. The other two sides are called legs. Hypotenuse Legs

HYPOTENUSE-LEG THEOREM Refer to as HL If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent

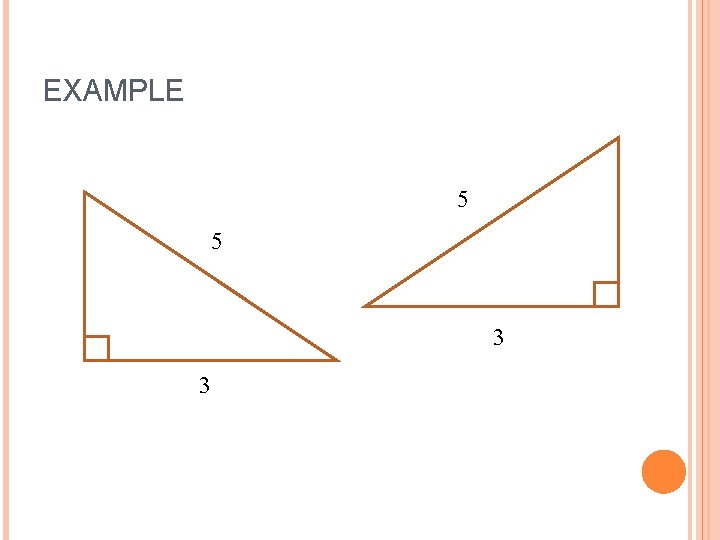
EXAMPLE 5 5 3 3

Example 4 A: Applying HL Congruence Determine if you can use the HL Congruence Theorem to prove the triangles congruent. If not, tell what else you need to know. According to the diagram, the triangles are right triangles that share one leg. It is given that the hypotenuses are congruent, therefore the triangles are congruent by HL.
 4-2 classifying triangles
4-2 classifying triangles Triangles classified by angles
Triangles classified by angles 4-2 classifying triangles
4-2 classifying triangles Classifying triangles by sides
Classifying triangles by sides How to classify a triangle by its sides with coordinates
How to classify a triangle by its sides with coordinates Lesson 4-1 classifying triangles answer key
Lesson 4-1 classifying triangles answer key 4-2 classifying triangles
4-2 classifying triangles Classifying triangles lesson plan
Classifying triangles lesson plan 4-2 classifying triangles
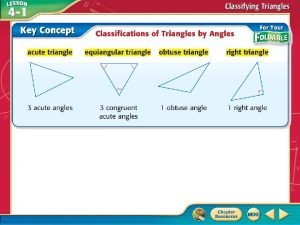
4-2 classifying triangles Classifying triangles by angle measures
Classifying triangles by angle measures Geometry classifying triangles
Geometry classifying triangles Trigonometry maze answer
Trigonometry maze answer Classifying triangles in the coordinate plane
Classifying triangles in the coordinate plane Classifying triangles 4-1
Classifying triangles 4-1 Lesson 4-1 classifying triangles
Lesson 4-1 classifying triangles Classifying triangles jeopardy game
Classifying triangles jeopardy game Classify the following triangle as acute obtuse or right
Classify the following triangle as acute obtuse or right Lesson 3 classify triangles
Lesson 3 classify triangles How to classify triangles
How to classify triangles Geometry
Geometry Two ways to classify triangles
Two ways to classify triangles Classify each molecule as an aldehyde, ketone, or neither.
Classify each molecule as an aldehyde, ketone, or neither. Classify each as carbohydrate protein or lipid
Classify each as carbohydrate protein or lipid Statically determinate truss
Statically determinate truss Chapter 6 review geometry
Chapter 6 review geometry Find the sum and then classify it.
Find the sum and then classify it. Continuous data vs discrete
Continuous data vs discrete Polynomial
Polynomial Classify each polynomial based on number of terms
Classify each polynomial based on number of terms Classify each process as spontaneous or nonspontaneous.
Classify each process as spontaneous or nonspontaneous. 10-1 solid geometry
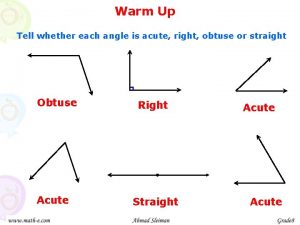
10-1 solid geometry Classify the angle as acute right obtuse or straight
Classify the angle as acute right obtuse or straight Classify each polynomial by its degree and number of terms
Classify each polynomial by its degree and number of terms Classify each decreasing function as having a slope
Classify each decreasing function as having a slope 6 quadrilaterals
6 quadrilaterals Tell whether each kind of angle is right acute or obtuse
Tell whether each kind of angle is right acute or obtuse Classify each as carbohydrate protein or lipid
Classify each as carbohydrate protein or lipid Classify each polynomial and determine its degree
Classify each polynomial and determine its degree