Classifying Triangles Angle Measures of Triangles Triangle A

Classifying Triangles Angle Measures of Triangles

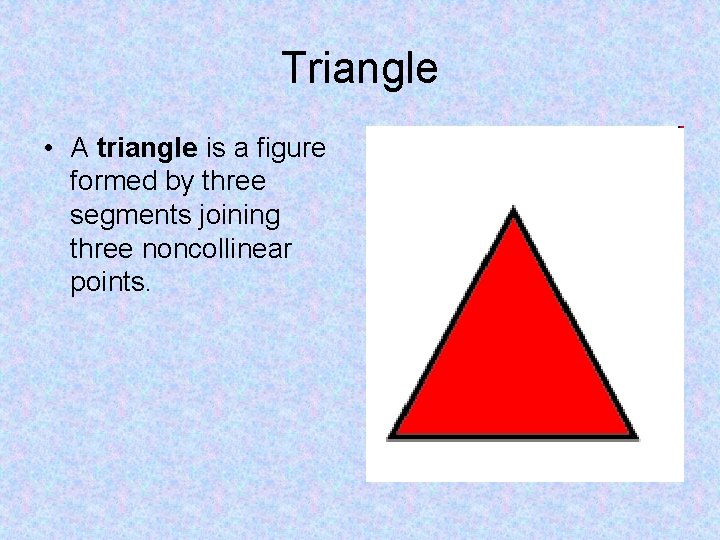
Triangle • A triangle is a figure formed by three segments joining three noncollinear points.

Classifying Triangles by Sides • Equilateral Triangle • Isosceles Triangle • Scalene Triangle

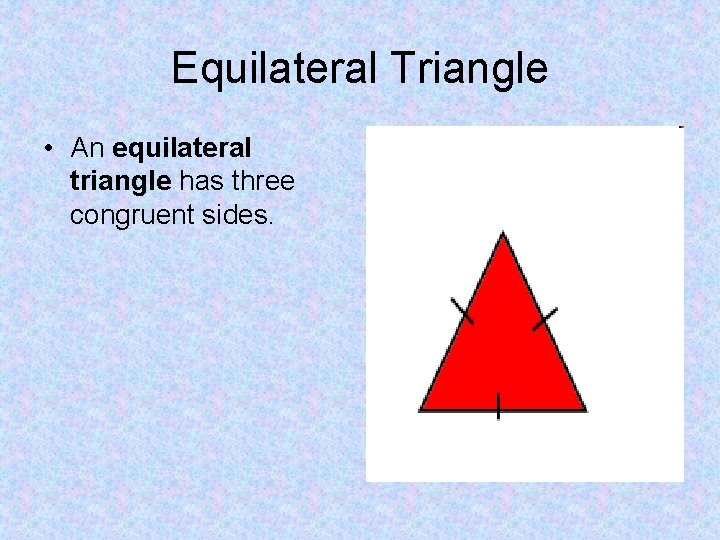
Equilateral Triangle • An equilateral triangle has three congruent sides.

Isosceles Triangle • An isosceles triangle has at least two congruent sides.

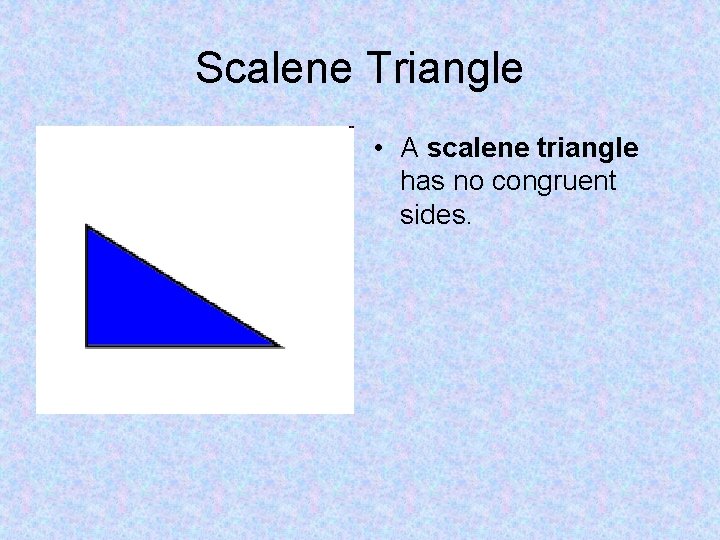
Scalene Triangle • A scalene triangle has no congruent sides.

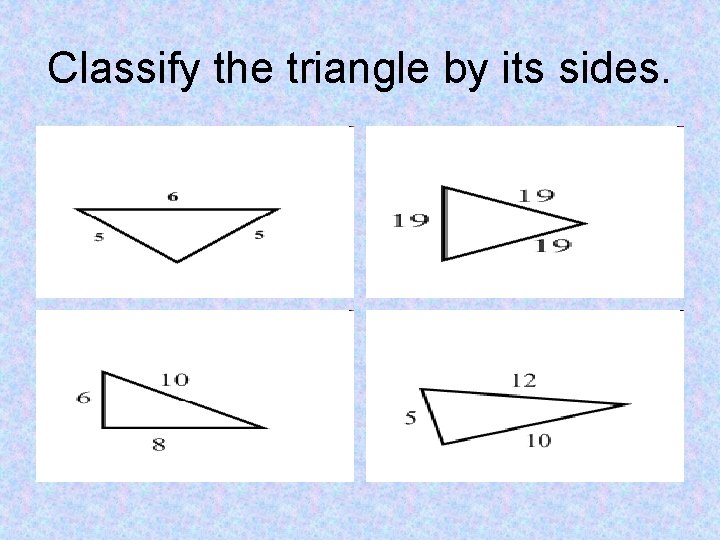
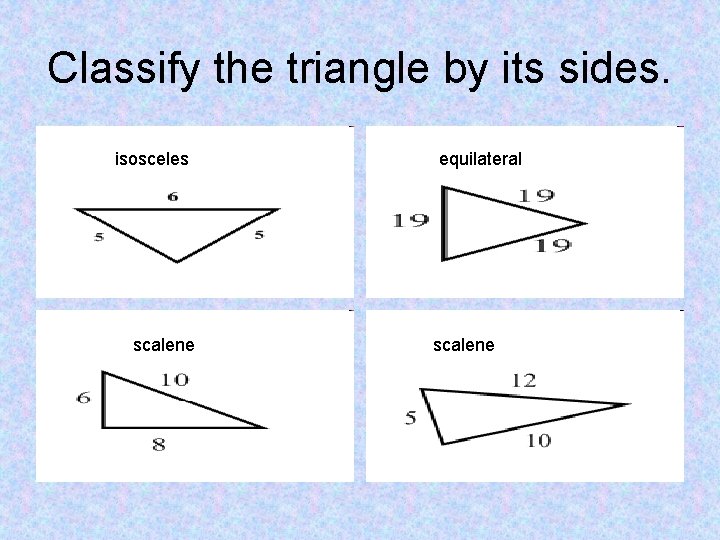
Classify the triangle by its sides.

Classify the triangle by its sides. isosceles scalene equilateral scalene

Classification of Triangles by Angles • • Equiangular triangle Acute triangle Right triangle Obtuse triangle

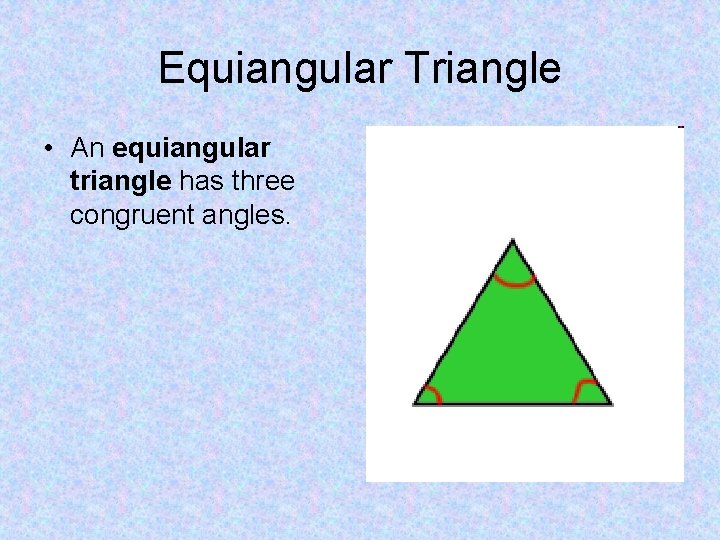
Equiangular Triangle • An equiangular triangle has three congruent angles.

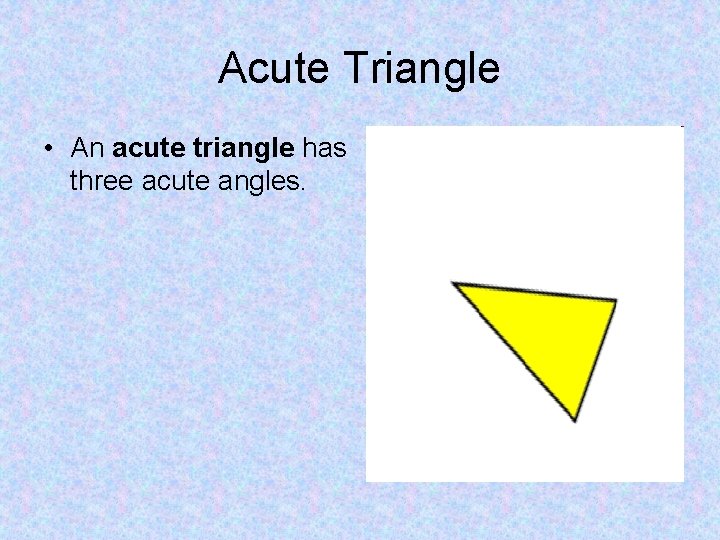
Acute Triangle • An acute triangle has three acute angles.

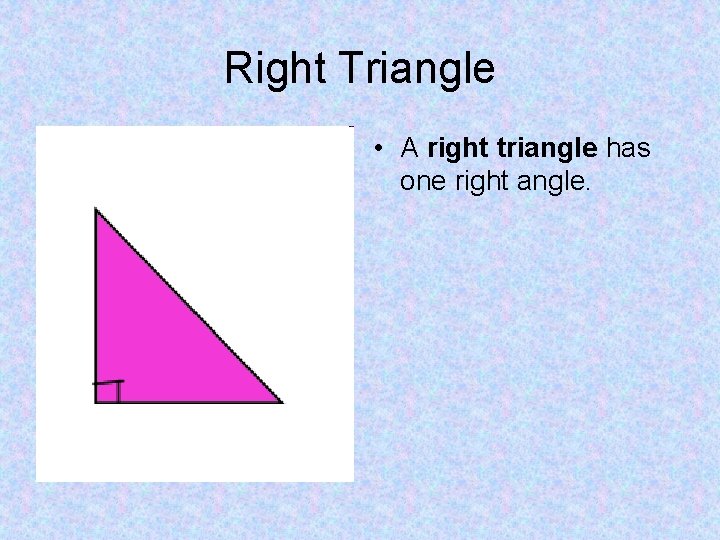
Right Triangle • A right triangle has one right angle.

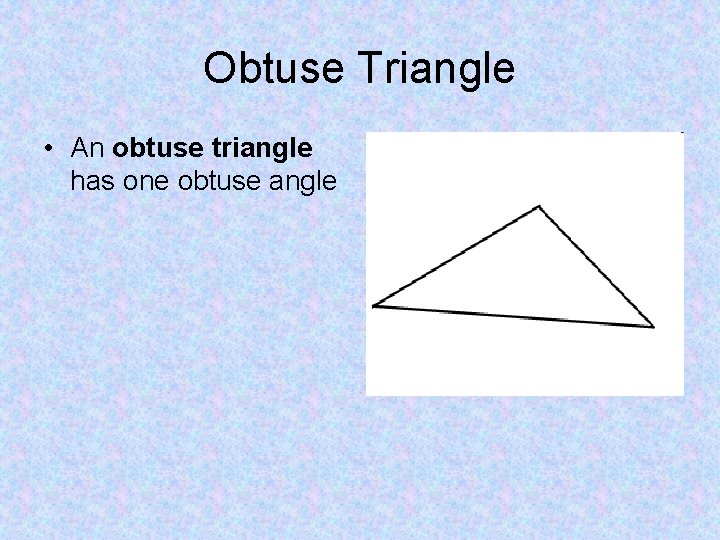
Obtuse Triangle • An obtuse triangle has one obtuse angle

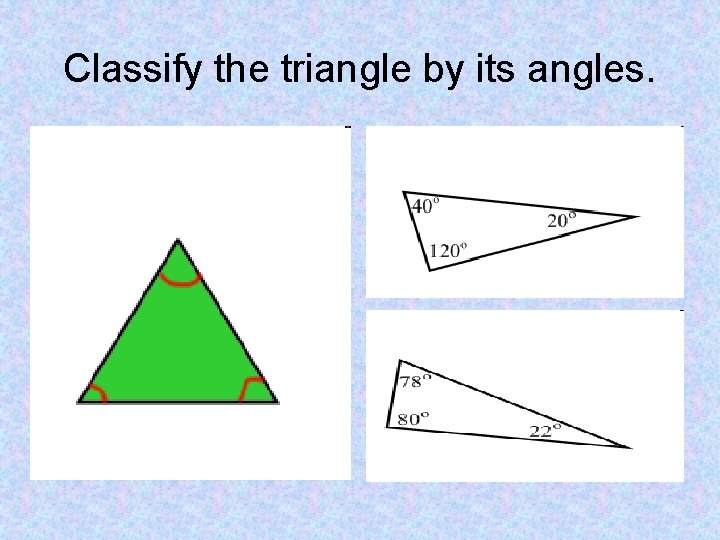
Classify the triangle by its angles.

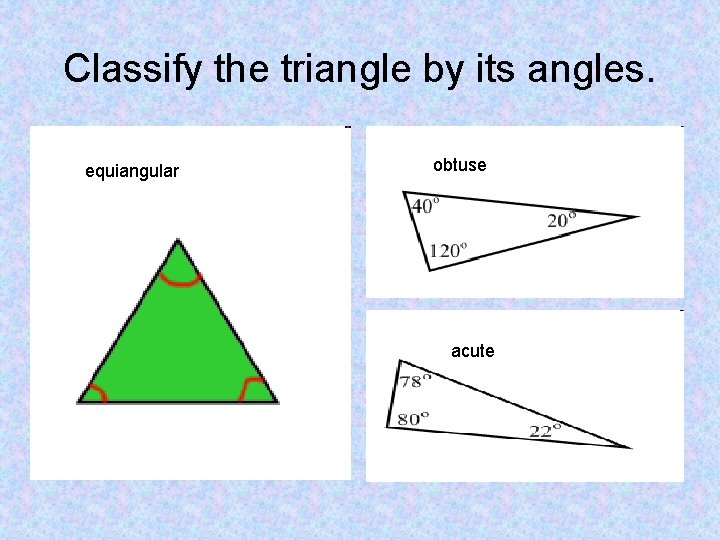
Classify the triangle by its angles. equiangular obtuse acute

Name that Triangle 1

Name that Triangle Sorry, this is not a triangle. 1

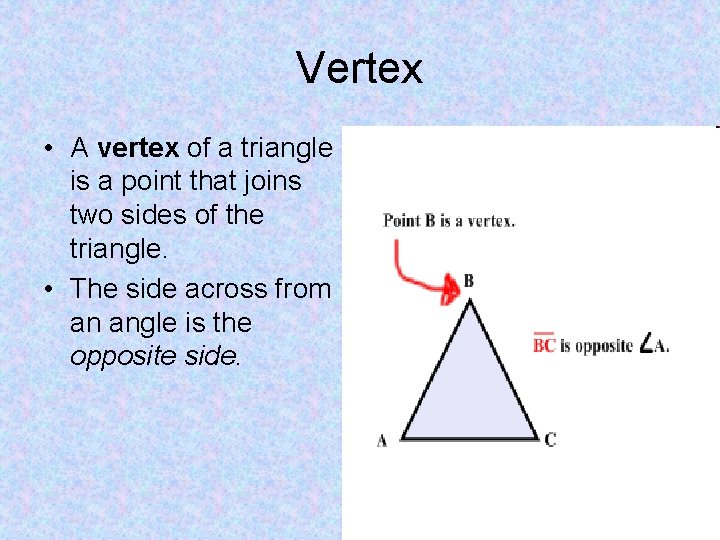
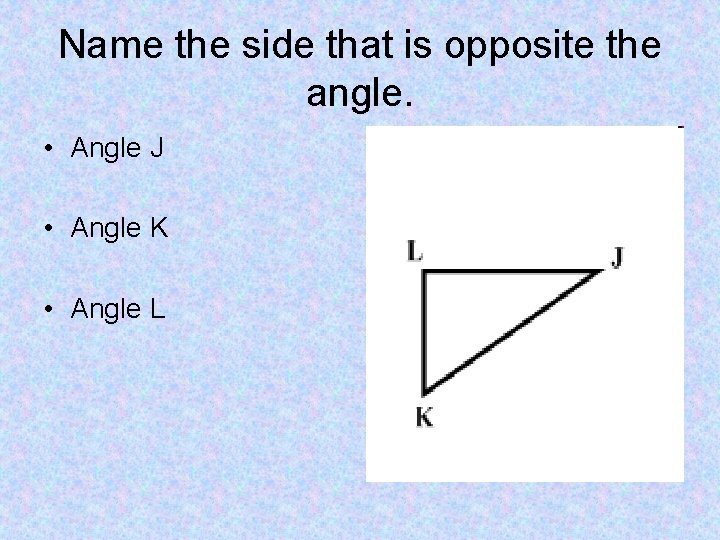
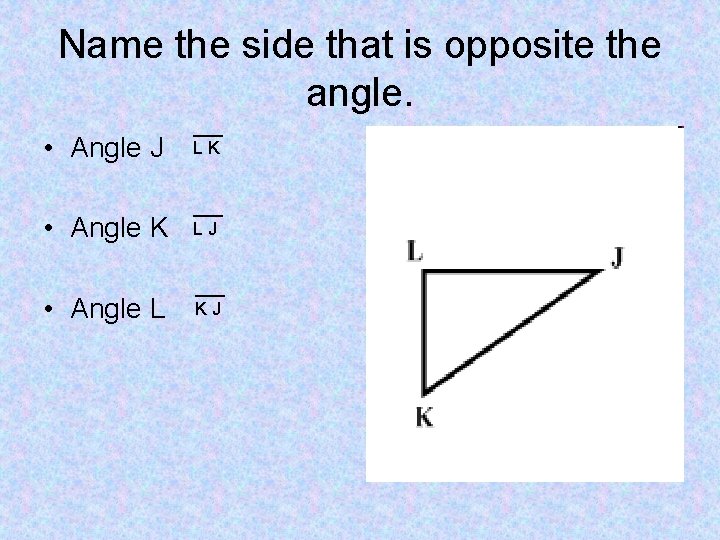
Vertex • A vertex of a triangle is a point that joins two sides of the triangle. • The side across from an angle is the opposite side.

Name the side that is opposite the angle. • Angle J • Angle K • Angle L

Name the side that is opposite the angle. • Angle J ___ LK • Angle K ___ LJ • Angle L ___ KJ

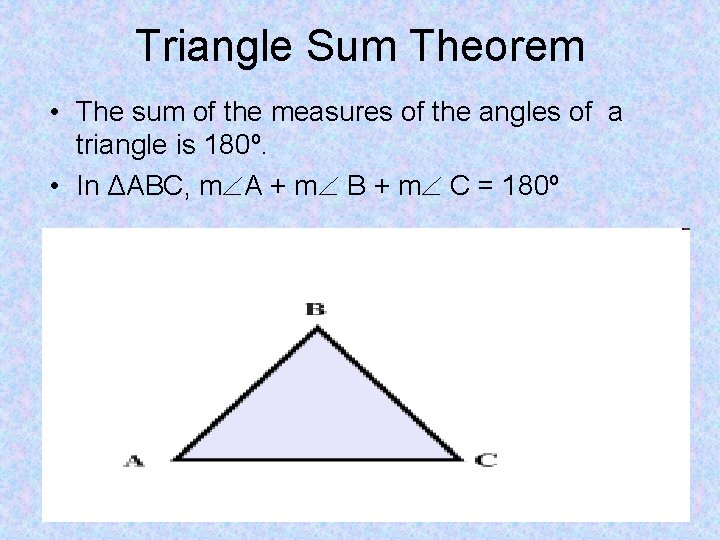
Triangle Sum Theorem • The sum of the measures of the angles of a triangle is 180º. • In ΔABC, m A + m B + m C = 180º

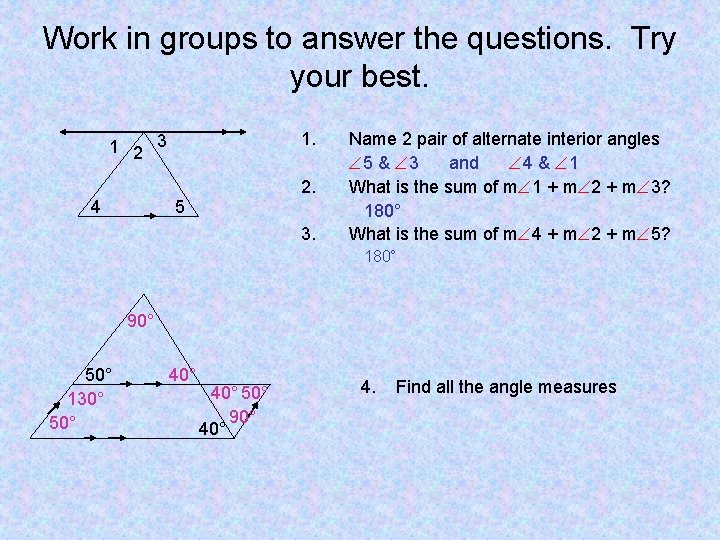
Work in groups to answer the questions. Try your best. 1. 1 2 3 2. 4 5 3. Name 2 pair of alternate interior angles 5 & 3 and 4 & 1 What is the sum of m 1 + m 2 + m 3? 180° What is the sum of m 4 + m 2 + m 5? 180° 90° 50° 130° 50° 40° 50° 90° 4. Find all the angle measures

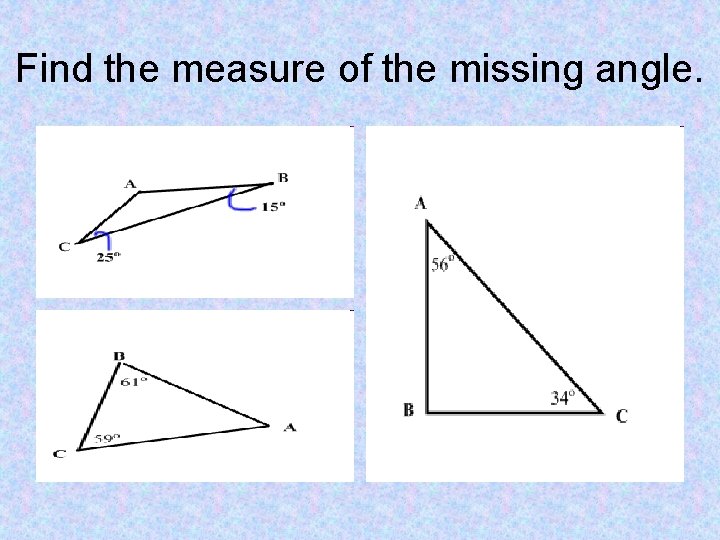
Find the measure of the missing angle.

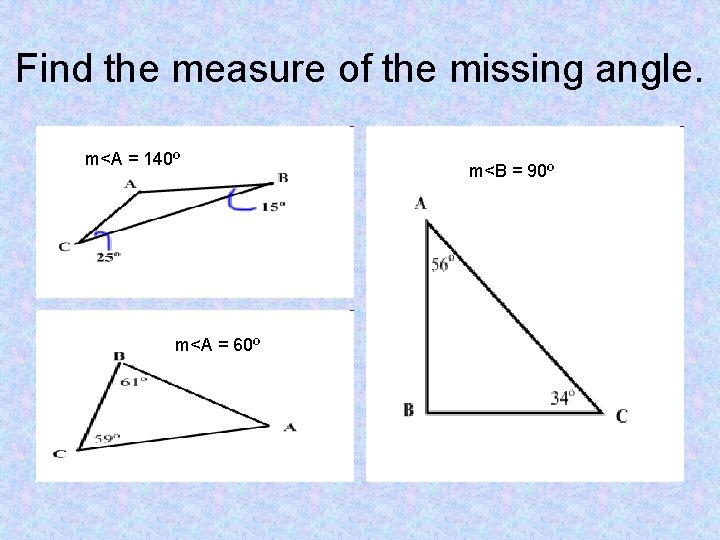
Find the measure of the missing angle. m<A = 140º m<A = 60º m<B = 90º

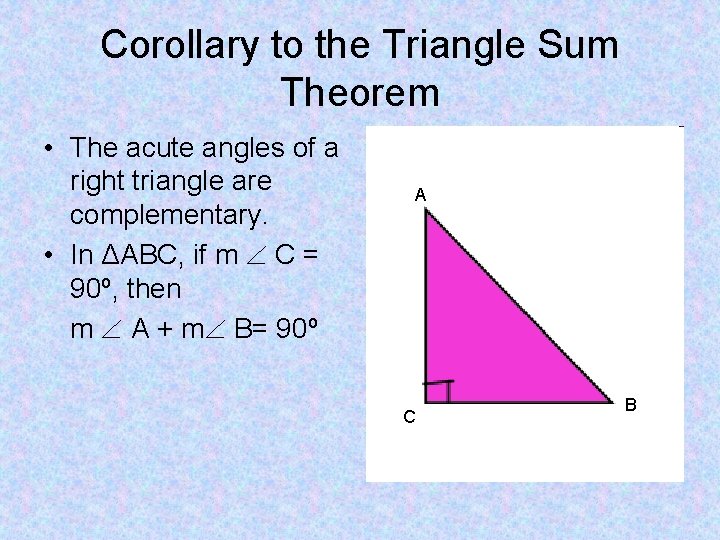
Corollary to the Triangle Sum Theorem • The acute angles of a right triangle are complementary. • In ΔABC, if m C = 90º, then m A + m B= 90º A C B

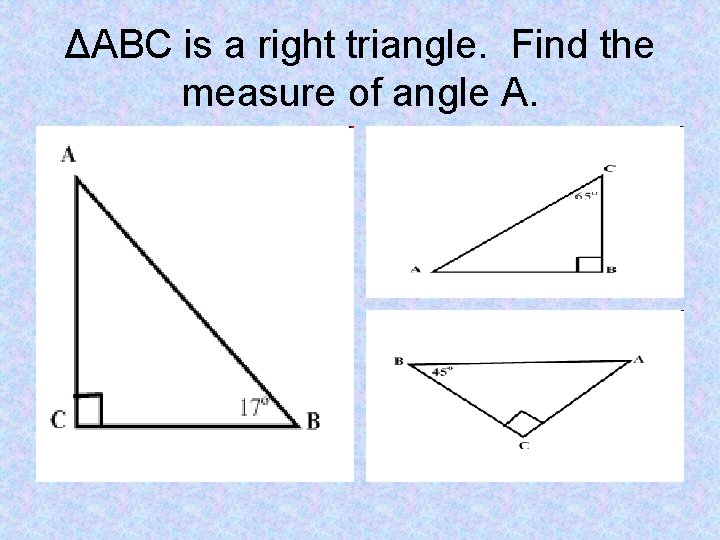
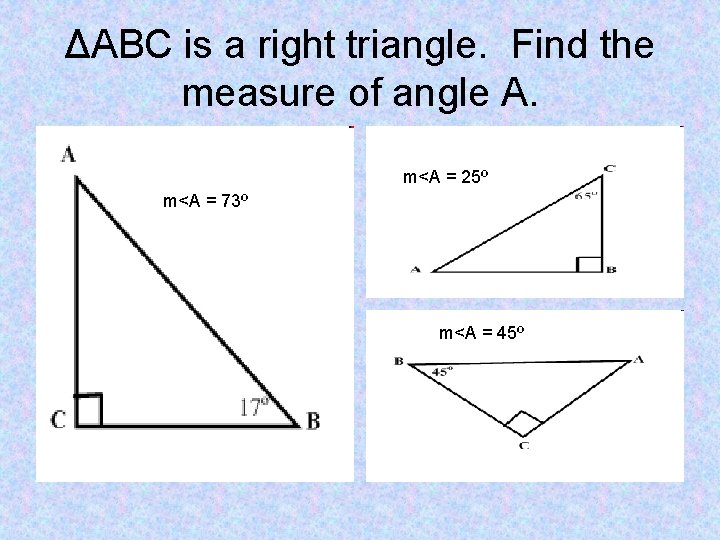
ΔABC is a right triangle. Find the measure of angle A.

ΔABC is a right triangle. Find the measure of angle A. m<A = 25º m<A = 73º m<A = 45º

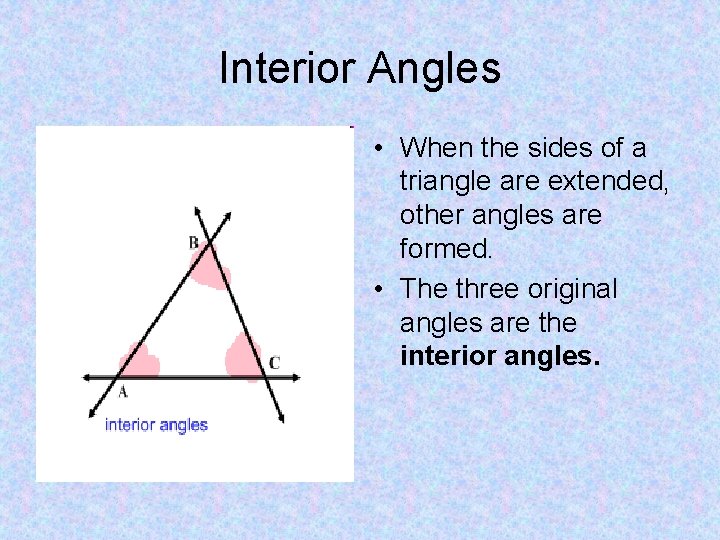
Interior Angles • When the sides of a triangle are extended, other angles are formed. • The three original angles are the interior angles.

Exterior Angles • The angles that are adjacent to the interior angles are the exterior angles. • It is common to show only one exterior angle at a vertex.

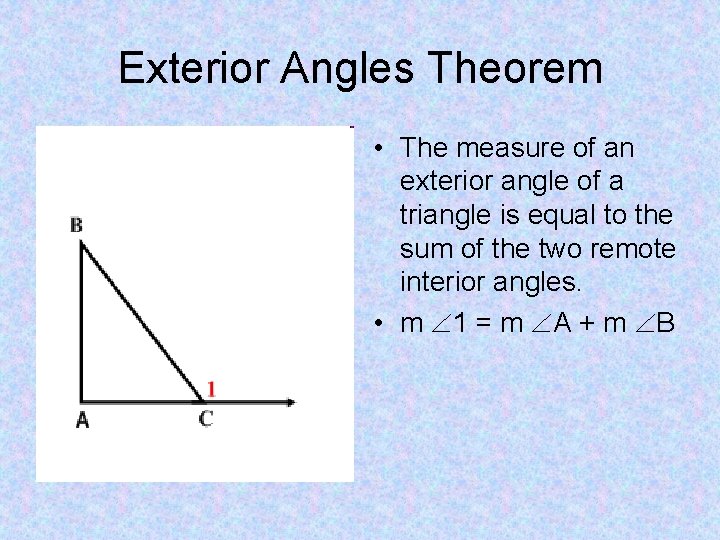
Exterior Angles Theorem • The measure of an exterior angle of a triangle is equal to the sum of the two remote interior angles. • m 1 = m A + m B

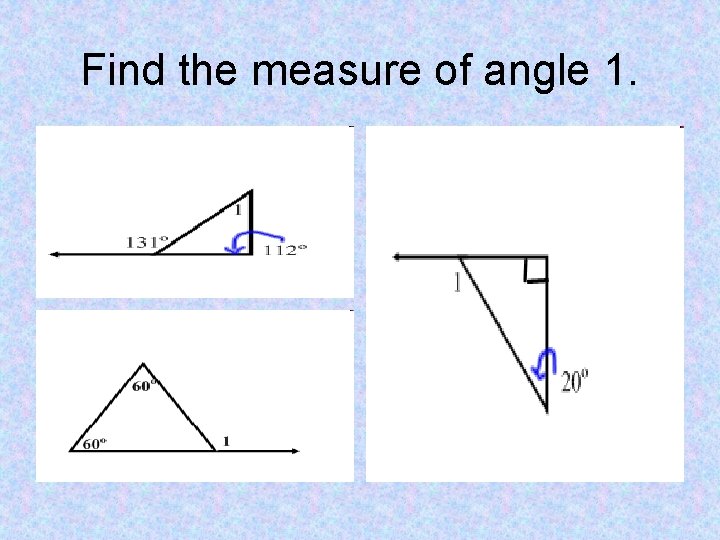
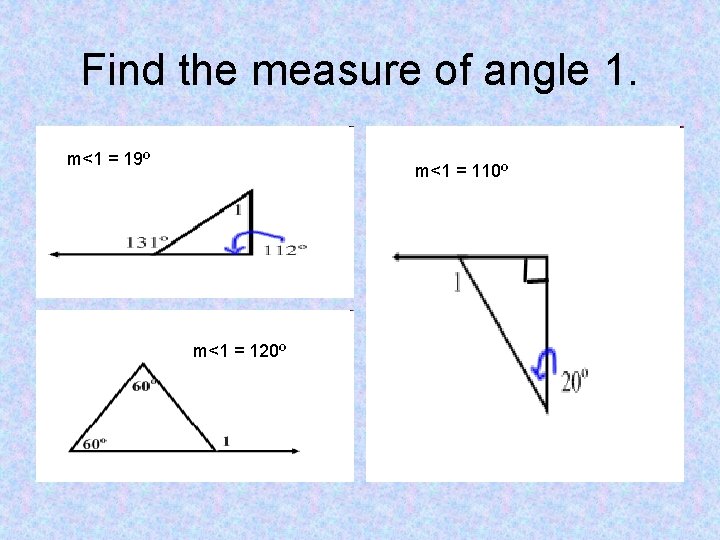
Find the measure of angle 1.

Find the measure of angle 1. m<1 = 19º m<1 = 110º m<1 = 120º