12 6 Segment Relationshipsinin Circles Holt Mc Dougal

12 -6 Segment. Relationshipsinin. Circles Holt. Mc. Dougal Geometry Holt

12 -6 Segment Relationships in Circles Learning Targets I will find the lengths of segments formed by lines that intersect circles. I will use the lengths of segments in circles to solve problems. Holt Mc. Dougal Geometry

12 -6 Segment Relationships in Circles Vocabulary secant segment external secant segment tangent segment Holt Mc. Dougal Geometry

12 -6 Segment Relationships in Circles Holt Mc. Dougal Geometry

12 -6 Segment Relationships in Circles Example 1: Applying the Chord-Chord Product Theorem Find the value of x and the length of each chord. EJ JF = GJ JH 10(7) = 14(x) 70 = 14 x 5=x EF = 10 + 7 = 17 GH = 14 + 5 = 19 Holt Mc. Dougal Geometry J

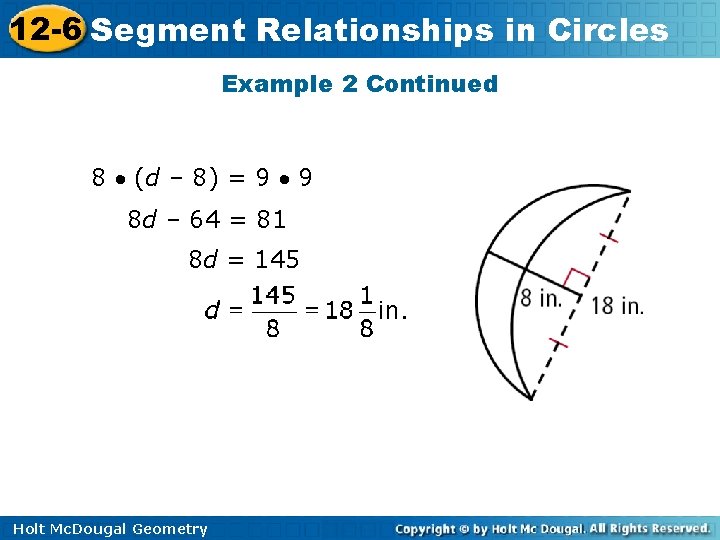
12 -6 Segment Relationships in Circles Example 2: Art Application The art department is contracted to construct a wooden moon for a play. One of the artists creates a sketch of what it needs to look like by drawing a chord and its perpendicular bisector. Find the diameter of the circle used to draw the outer edge of the moon. Holt Mc. Dougal Geometry

12 -6 Segment Relationships in Circles Example 2 Continued 8 (d – 8) = 9 9 8 d – 64 = 81 8 d = 145 Holt Mc. Dougal Geometry

12 -6 Segment Relationships in Circles A secant segment is a segment of a secant with at least one endpoint on the circle. An external secant segment is a secant segment that lies in the exterior of the circle with one endpoint on the circle. Holt Mc. Dougal Geometry

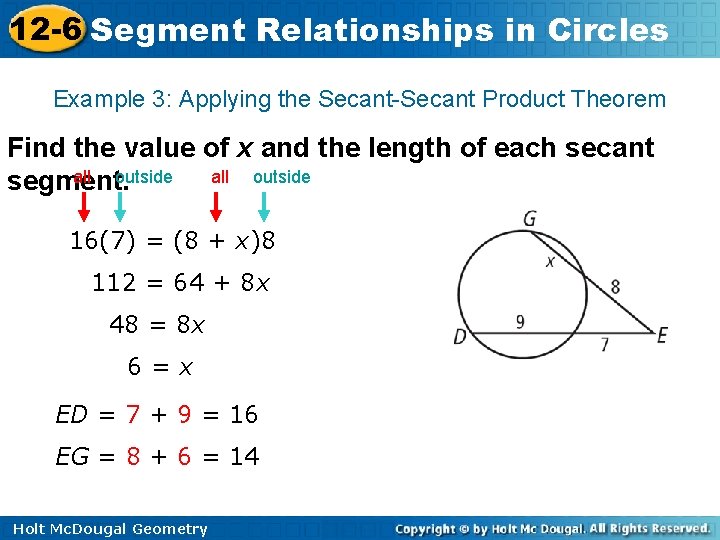
12 -6 Segment Relationships in Circles In words: ALL times OUTSIDE equals ALL times OUTSIDE Holt Mc. Dougal Geometry

12 -6 Segment Relationships in Circles Example 3: Applying the Secant-Secant Product Theorem Find the value of x and the length of each secant all outside segment. 16(7) = (8 + x)8 112 = 64 + 8 x 48 = 8 x 6=x ED = 7 + 9 = 16 EG = 8 + 6 = 14 Holt Mc. Dougal Geometry

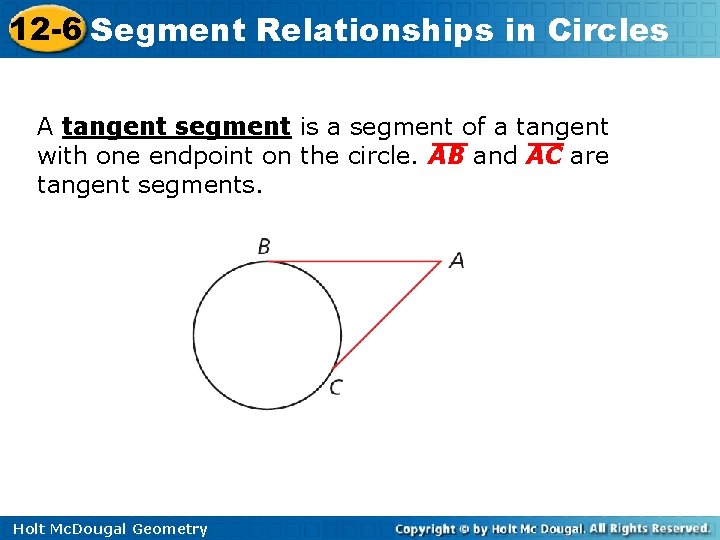
12 -6 Segment Relationships in Circles A tangent segment is a segment of a tangent with one endpoint on the circle. AB and AC are tangent segments. Holt Mc. Dougal Geometry

12 -6 Segment Relationships in Circles The words ALL times OUTSIDE equals ALL times OUTSIDE still apply, as the entire tangent segment is outside the circle. Holt Mc. Dougal Geometry

12 -6 Segment Relationships in Circles Example 4: Applying the Secant-Tangent Product Theorem Find the value of x. ML JL = KL 2 20(5) = x 2 100 = x 2 ± 10 = x The value of x must be 10 since it represents a length. Holt Mc. Dougal Geometry

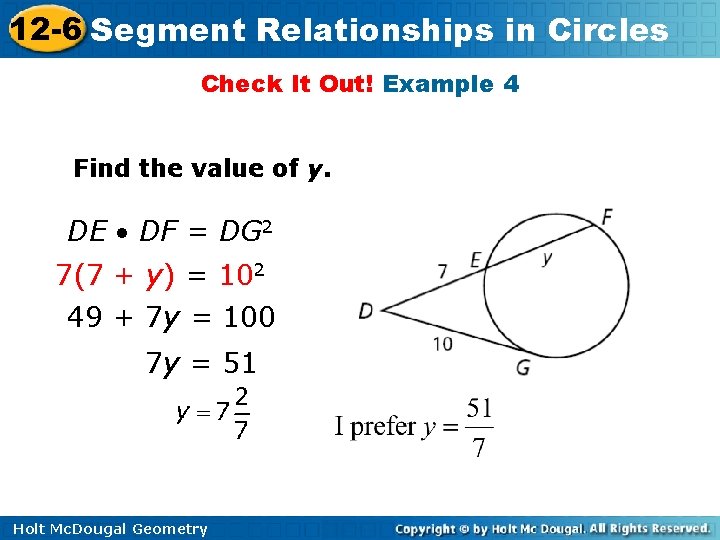
12 -6 Segment Relationships in Circles Check It Out! Example 4 Find the value of y. DE DF = DG 2 7(7 + y) = 102 49 + 7 y = 100 7 y = 51 Holt Mc. Dougal Geometry

12 -6 Segment Relationships in Circles HOMEWORK: Pages 843 – 844, #6 – 14, 16 - 23 Holt Mc. Dougal Geometry