1 Strain and Strain Displacement relations Cauchys Equations

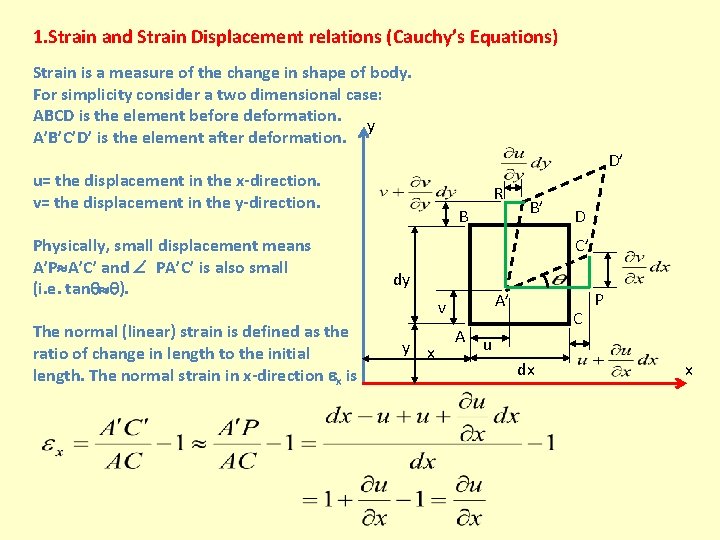
1. Strain and Strain Displacement relations (Cauchy’s Equations) Strain is a measure of the change in shape of body. For simplicity consider a two dimensional case: ABCD is the element before deformation. y A’B’C’D’ is the element after deformation. D’ u= the displacement in the x-direction. v= the displacement in the y-direction. Physically, small displacement means A’P A’C’ and PA’C’ is also small (i. e. tan ). The normal (linear) strain is defined as the ratio of change in length to the initial length. The normal strain in x-direction x is R B B’ D C’ dy A’ v y x A C P u dx x

Similarly Shear strain is defined as the change in angle between two lines originally at right angle. The shear strain is ( RA’B’ + PA’C’) Since 1

(engineering shear strain) Mathematical shear strain is equal to half engineering shear strain. In the case of three dimensions, is the displacement in the z-direction, then These relationships are called Cauchy’s equations.

The full expressions for the strain components at a point could be defined by the strain matrix, that is Where,

2. Strain Transformations Transformation of strain from one set of reference axes to another set follows a development identical to that of stresses. The resulting expressions take the following forms, and, (1) (2) In the above equations the mathematical definition of shear strain is used since these are tensor transformation,

The equivalent transformation in terms of , became, (3) (4) As with stresses, there exists a set of axes along which the shear strains are zero. These are the principal strain axes and these normal strains are principal strains.

Where one axis common to both sets of axes (i. e. , z and z’ coincide), strain transformations take the form, (5) (6) (7) In terms of principal strains several useful relations are, (8) (9) (10)

Note; eq. (1) can be written in the following form, Example(1): The sketch below shows three wire resistance strain gages attached to the surface of a part. Under load, the gages give the following indications of strains, Gage(a) = 0. 002 cm/cm Gage(b) = 0. 0025 cm/cm Gage(c) = 0. 0005 cm/cm Find the magnitude of xy and of y principal strains in the x-y plane. (c) x’ (b) 300 (a) x

Solution: Using eq. (3), where lx’x = cos 30 o and lx’y =cos 60 o 0. 0025 = 0. 002 (0. 866)2 + 0. 0005(0. 5)2 + xy (0. 866)(0. 5) xy = 0. 00202 cm/cm To find the principal strains, eqs. (3) and (4) can be rearranged in a manner that to give, Therefore,

3. Relationships between stress an strain (Generalized Hooke’s Low) Hooke’s Low: For an elastic material the strain produced is proportional to the applied stress. For a linear elastic material the principle of superposition applies. The effect of normal stress is to produce normal strains. The normal strains are unaffected by the shear stresses but shear strains are produced by shear stresses. The complete stress-strain relationships are: (11) (12) (13)

Where, E = Young’s modulus of elasticity = Poisson’s ratio G = Modulus of rigidity The elastic constants E, , G are related by:

4. Compatibility Equations (Saint-Venant’s Equations) If u(x, y, z), v(x, y, z) and w(x, y, z) are given, then the whole six strain components can be derived by differentiation. Compatibility is satisfied automatically. If the six strains x(x, y, z), y(x, y, z), z(x, y, z), xy(x, y, z), yz(x, y, z), and zx(x, y, z) are given, the three displacement components u(x, y, z), v(x, y, z), and w(x, y, z) can be determined uniquely if and only if relations exist among the strains. (14) (15) But since (16) (17)

(18) (19) Also from Cauchy’s equations

(20) Similarly (21) and (22) In terms of stresses, if there are no body forces or if the forces are constants, the compatibility equation 17 to 22 become

Laplacian operator