Week 3 Values and Types Types of values

Week 3 Values and Types § Types of values. § Primitive, composite, recursive types. § Type systems: static vs dynamic typing, type completeness. § Expressions. § Implementation notes. © 2004, D. A. Watt, University of Glasgow 2 -1

Composite types § A composite value is one that is composed from simpler values. § A composite type is a type whose values are composite. § PLs support a huge variety of composite types. § All these can be understood in terms of a few concepts: • Cartesian products (tuples, structures, records) • mappings (arrays) • disjoint unions (algebraic data types, discriminated records, objects) • recursive types (lists, trees, etc. ) 2 -2

Mappings (1) § We write m : S T to state that m is a mapping from set S to set T. In other words, m maps every value in S to some value in T. § If m maps value x to value y, we write y = m(x). The value y is called the image of x under m. § Some of the mappings in {u, v} {a, b, c}: m 1 = {u a, v c} m 2 = {u c, v c} m 3 = {u c, v b} image of u is c, image of v is b 2 -3

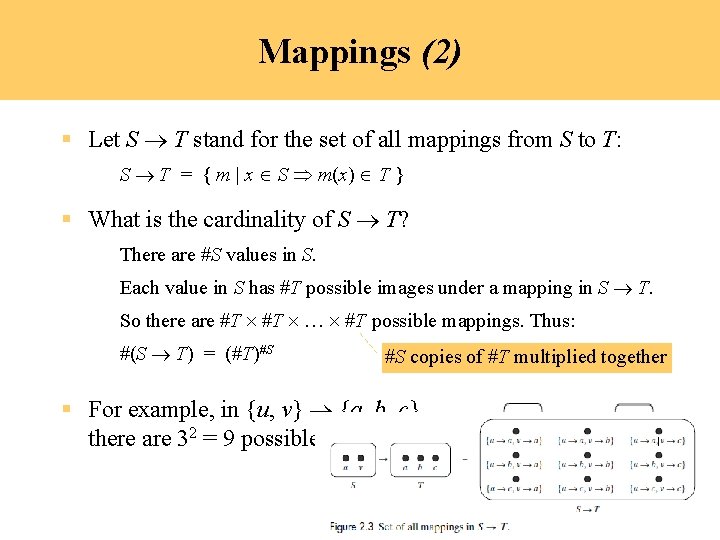
Mappings (2) § Let S T stand for the set of all mappings from S to T: S T = { m | x Î S Þ m(x) Î T } § What is the cardinality of S T? There are #S values in S. Each value in S has #T possible images under a mapping in S T. So there are #T … #T possible mappings. Thus: #(S T) = (#T)#S #S copies of #T multiplied together § For example, in {u, v} {a, b, c} there are 32 = 9 possible mappings. 2 -4

Arrays (1) § Arrays (found in all imperative and OO PLs) can be understood as mappings. § If an array’s components are of type T and its index values are of type S, the array has one component of type T for each value in type S. Thus the array’s type is S T. § An array’s length is the number of components, #S. § Basic operations on arrays: • construction of an array from its components • indexing – using a computed index value to select a component. so we can select the ith component 2 -5

Arrays (1) § Arrays (found in all imperative and object oriented PLs) can be understood as mappings. § If an array’s components are of type T and its index values are of type S • the array has one component of type T for each value in type S. • Thus the array’s type is S T. § An array’s length is the number of components, #S. § Basic operations on arrays: • construction of an array from its components • indexing – using a computed index value to select a component. so we can select the ith component 2 -6

Cardinality of Mappings(example) § Consider the C++ declaration: bool p[3]; § The set of all possible values of this array is {0, 1, 2} → {false, true} 2 -7

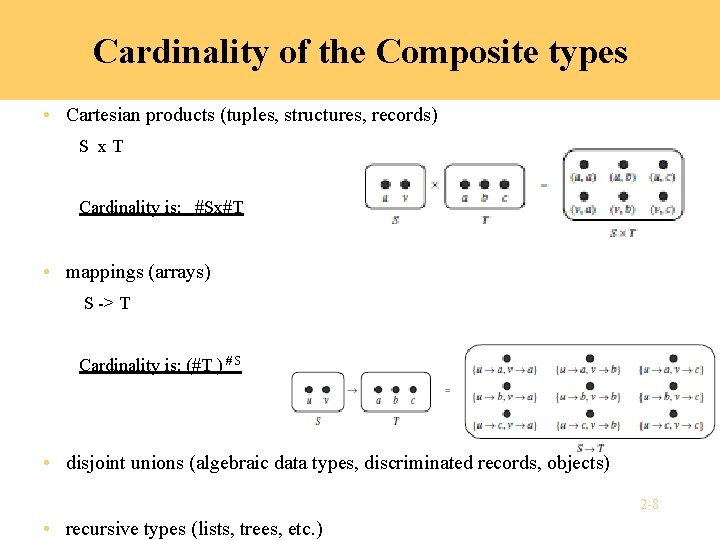
Cardinality of the Composite types • Cartesian products (tuples, structures, records) S x. T Cardinality is: #Sx#T • mappings (arrays) S -> T Cardinality is: (#T ) # S • disjoint unions (algebraic data types, discriminated records, objects) 2 -8 • recursive types (lists, trees, etc. )

Arrays (2) § An array of type S T is a finite mapping. § Here S is nearly always a finite range of consecutive values {l, l+1, …, u}. This is called the array’s index range. lower bound upper bound § In C and Java, the index range must be integers {0, 1, …, n– 1}. § How about multi-dimensional arrays? • If an array has index ranges of types S 1, …, Sn, the array’s type is S 1 … Sn T. 2 -9

Example: C++ arrays § Type declarations: bool Has. Employment[3]; § Application code: Has. Employment[1]=false; indexing int c=0; Has. Employment[c] = !Has. Employment[c]; bool Has. Employment[] = {true, false, true}; indexing array construction 2 -10

Example: Perl arrays § No type declarations in Perl and Python! § Perl’s Array construction: @mycolors = (‘red’, ‘green’, ‘blue’); § $mycolors[1] = ‘blue’; array construction indexing 2 -11

A special array type in Perl: Hash (also called Associative Arrays) § For set of values Color Boolean = {red, green, blue} {0, 1} § Define Hash type in Perl: %Pixel= ( “red”=> 0, “green”=>1, ”blue”=>0); This is same as: $Pixel{“red”}=0 $Pixel{“green”}=1 $Pixel{“blue”}=0 § Cardinality of Pixel : #Pixel = (#Boolean)#Color = 23 = 8 2 -12

Example: Perl multi-dimensional arrays § A 3 -dimensional Perl array $My. Window[0][2]{“red”}=1; § Set of values: %Pixel= ( “red”=> 0, “green”=>1, ”blue”=>0); Window = Yrange Xrange Pixel = {0, 1, …, 255} {0, 1, …, 511} Pixel § Cardinality: #Window = (2) 256 x 512 x 3 =(#Pixel)#Yrange #Xrange = 8256 512 2 -13

Functions are also mappings § Functions (found in all PLs) can also be understood as mappings. A function maps its argument(s) to its result. § If a function has a single argument of type S and its result is of type T, the function’s type is S T. § Basic operations on functions: • construction (or definition) of a function • application – calling the function with a computed argument. § We can generalize to functions with n arguments. • If a function has arguments of types S 1, …, Sn and its result type is T • The function’s type is S 1 … Sn T. 2 -14

Mathematical Function or Function Procedure? § A function procedure that inspects or modifies global variables does not correspond to any mathematical function. • i. e. a function procedure that returns the current time of day – this is function procedure • i. e. a function that computes and returns a random number – this is mathematical function § When using the term function in the context of programming languages, we must be very clear whether • Do we mean a mathematical function (mapping)? • Do we mean a function procedure? 2 -15

Example: C++ functions § Definition: bool is. Even (int n) { return (n % 2 == 0); } This function implements one particular mapping in Integer→Boolean, namely: {. . . , 0 → true, 1 → false, 2 → true, 3 → false, . . . } § Type: Integer Boolean § Value: {…, 0 true, 1 false, 2 true, 3 false, …} § Other functions of same type: is. Odd, is. Prime, etc. 2 -16

Finally… Some Discussion… Quiz : Which of these constitute plagiarism? 1. Copying your friend’s introduction/code, changing a few lines and Yes variables? 2. Copying a figure from your previous paper? No 3. Watching your classmate write a program, then going Yes home and writing your own program from memory? Yes 4. Reusing terms defined in a paper you reviewed and 5. rejected? Submitting a paper to two different journals at the same Yes time? 6. Forgetting where you read something, so omitting the Yes reference? 7. Adding additional material to your conference paper and No submitting the expanded paper to a journal? 8. Copying background paragraphs from your advisor’s paper 17 -Sep-20 into your dissertation? © Offutt 2003 -2014 Yes 17