Vertex Form of Quadratics We already know We

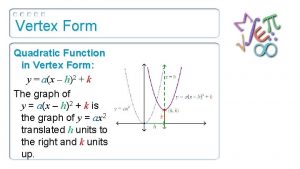
Vertex Form of Quadratics

We already know: We are learning today:

Why is knowing vertex form important if we already know standard form? ? If an equation is in vertex form you should be able to state the axis of symmetry & vertex form with no work.

This is a HIGHLY questioned area of the EOC we will take in may. It will typically appear on the NO CALCULATOR section.

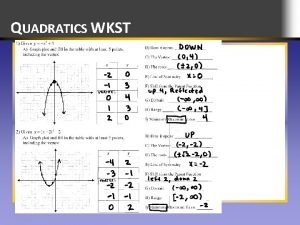
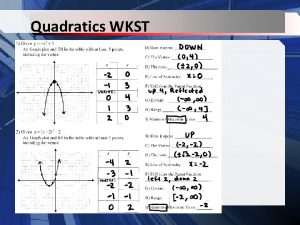
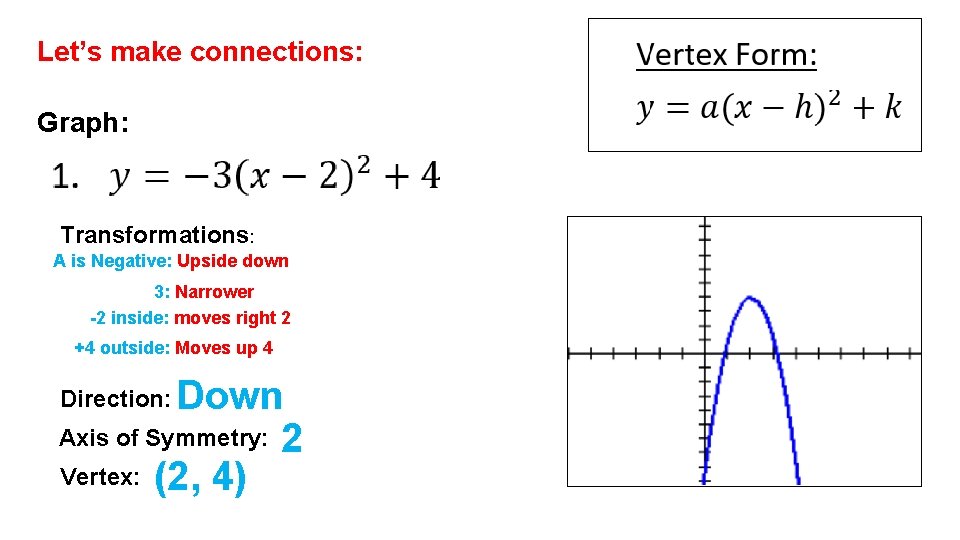
Let’s make connections: Graph: Transformations: A is Negative: Upside down 3: Narrower -2 inside: moves right 2 +4 outside: Moves up 4 Down Axis of Symmetry: 2 Vertex: (2, 4) Direction:

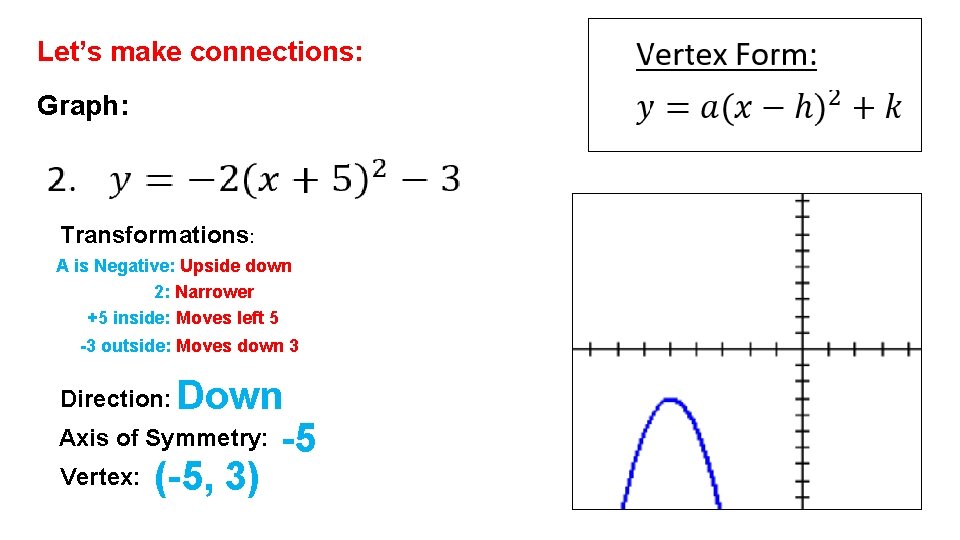
Let’s make connections: Graph: Transformations: A is Negative: Upside down 2: Narrower +5 inside: Moves left 5 -3 outside: Moves down 3 Down Axis of Symmetry: -5 Vertex: (-5, 3) Direction:

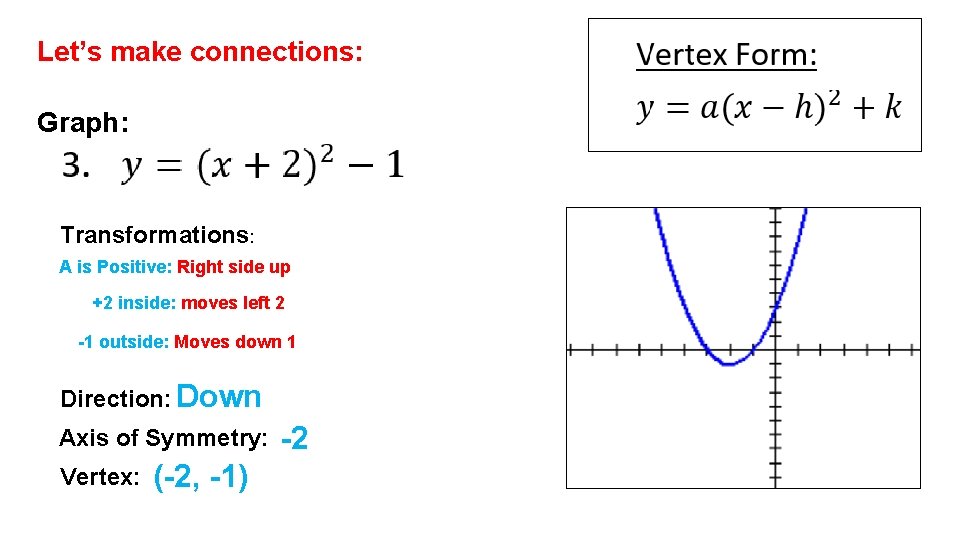
Let’s make connections: Graph: Transformations: A is Positive: Right side up +2 inside: moves left 2 -1 outside: Moves down 1 Direction: Down Axis of Symmetry: Vertex: (-2, -1) -2

Let’s make connections: Based off our answer for the last three questions what does each part of vertex form mean? a: Direction (up or down – positive or negative) Axis of Sym. is OPPOSITE h: of that number k: Vertex is (-h, k)

A FUN way to remember what “h” does is…. The HOP-posite! H is the OPPOSITE of the axis of symmetry.

Name the direction, axis of symmetry and vertex of each equation. WITHOUT A CALCULATOR. Direction: UP Axis of Sym. : Vertex: -1 (-1, 4) Direction: DOWN Axis of Sym. : Vertex: 7 (7, -2)

Name the direction, axis of symmetry and vertex of each equation. WITHOUT A CALCULATOR. Direction: DOWN Axis of Sym. : Vertex: -4 (-4, 1) Direction: UP Axis of Sym. : Vertex: 2 (2, 0)

Name the direction, axis of symmetry and vertex of each equation. WITHOUT A CALCULATOR. Direction: UP Axis of Sym. : Vertex: -8 (-8, -2) Direction: UP Axis of Sym. : Vertex: -4 (-4, -9)