VERTEX FORM OF QUADRATICS WE ALREADY KNOW WE

VERTEX FORM OF QUADRATICS

WE ALREADY KNOW: WE ARE LEARNING TODAY: VERTEX FORM (VERTICAL PARABOLA): OR SOMETIMES WRITTEN AS: *THE ONLY DIFFERENCE BETWEEN THE TWO IS WHICH SIDE K IS *THE MOST IMPORTANT THING TO PAY ATTENTION TO IS THE SIGNS FOR H AND K

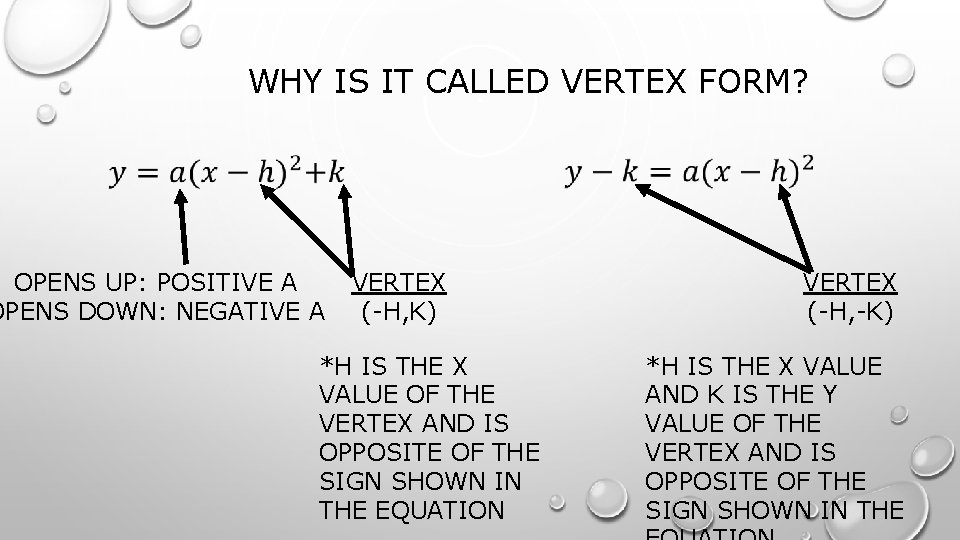
WHY IS IT CALLED VERTEX FORM? OPENS UP: POSITIVE A OPENS DOWN: NEGATIVE A VERTEX (-H, K) *H IS THE X VALUE OF THE VERTEX AND IS OPPOSITE OF THE SIGN SHOWN IN THE EQUATION VERTEX (-H, -K) *H IS THE X VALUE AND K IS THE Y VALUE OF THE VERTEX AND IS OPPOSITE OF THE SIGN SHOWN IN THE

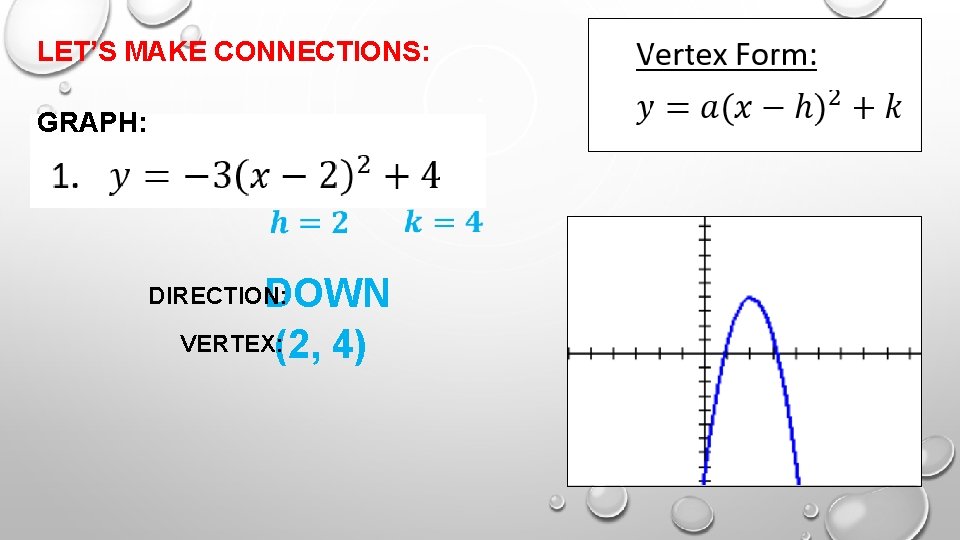
LET’S MAKE CONNECTIONS: GRAPH: DOWN VERTEX: (2, 4) DIRECTION:

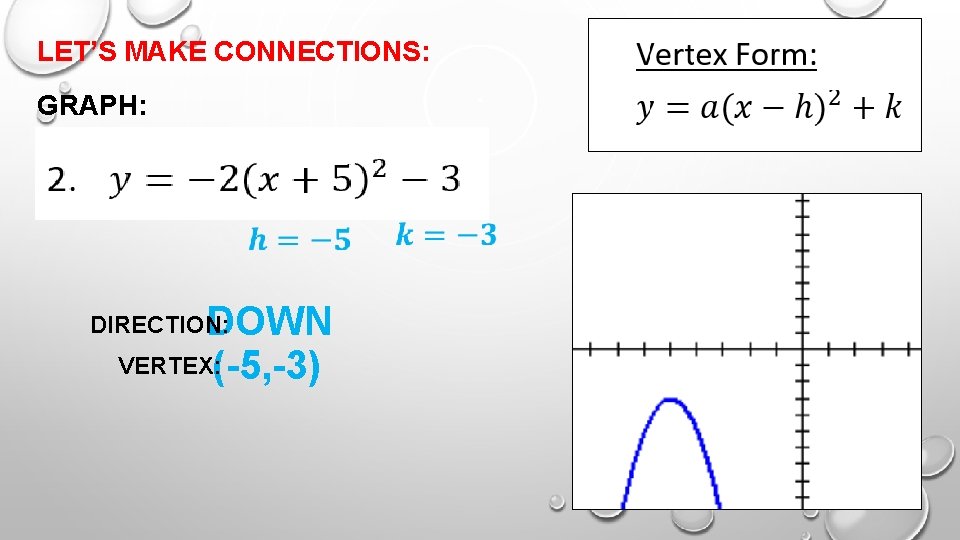
LET’S MAKE CONNECTIONS: GRAPH: DOWN VERTEX: (-5, -3) DIRECTION:

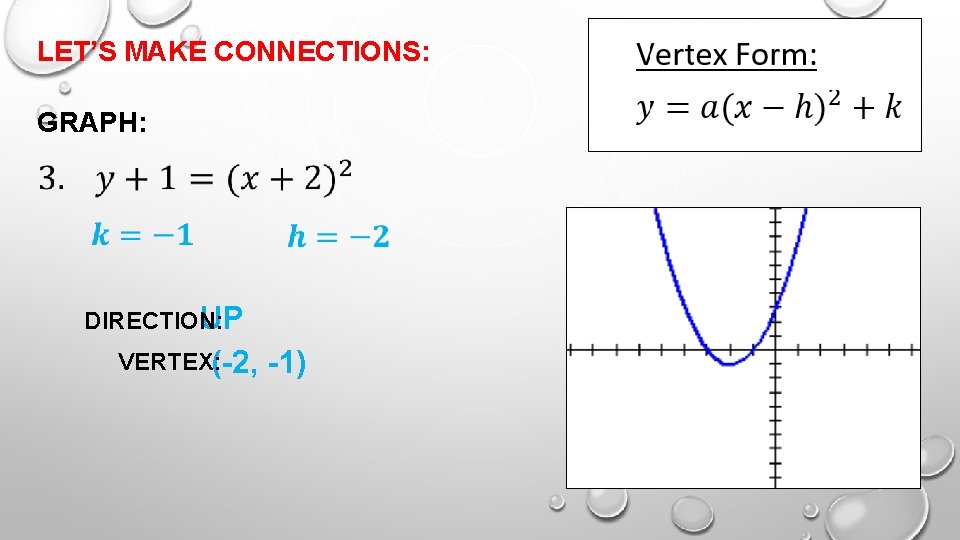
LET’S MAKE CONNECTIONS: GRAPH: DIRECTION: UP VERTEX: (-2, -1)

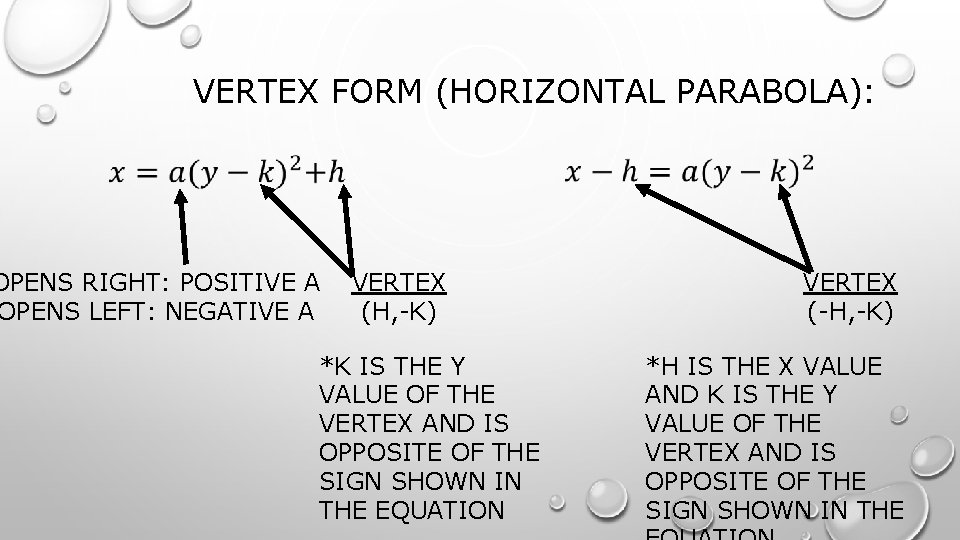
VERTEX FORM (HORIZONTAL PARABOLA): OR SOMETIMES WRITTEN AS: *THE DIFFERENCE BETWEEN VERTICAL AND HORIZONTAL PARABOLA IS: • X AND Y ARE SWITCHED • H AND K ARE SWITCHED o H STILL CORRESPONDS WITH X, AND K STILL CORRESPONDS WITH Y

VERTEX FORM (HORIZONTAL PARABOLA): OPENS RIGHT: POSITIVE A OPENS LEFT: NEGATIVE A VERTEX (H, -K) *K IS THE Y VALUE OF THE VERTEX AND IS OPPOSITE OF THE SIGN SHOWN IN THE EQUATION VERTEX (-H, -K) *H IS THE X VALUE AND K IS THE Y VALUE OF THE VERTEX AND IS OPPOSITE OF THE SIGN SHOWN IN THE

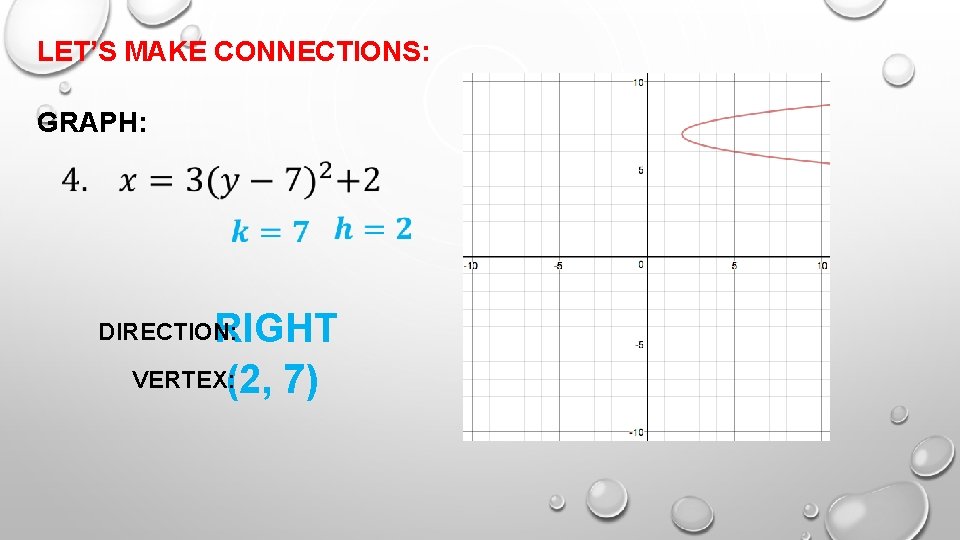
LET’S MAKE CONNECTIONS: GRAPH: RIGHT VERTEX: (2, 7) DIRECTION:

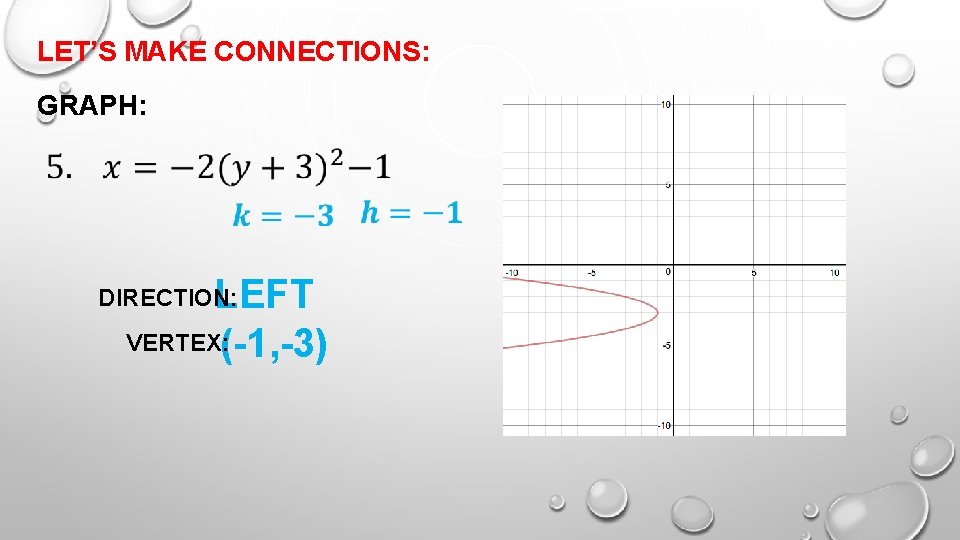
LET’S MAKE CONNECTIONS: GRAPH: LEFT VERTEX: (-1, -3) DIRECTION:

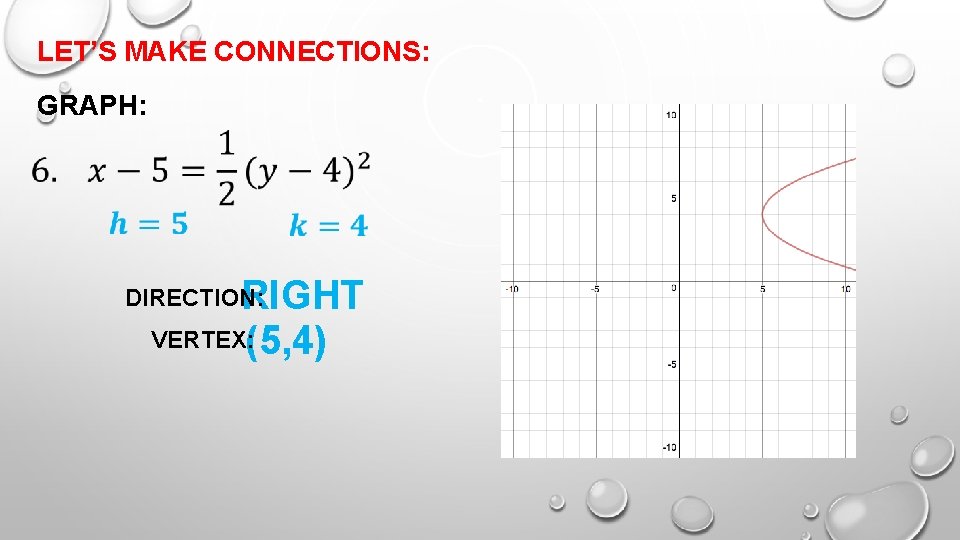
LET’S MAKE CONNECTIONS: GRAPH: RIGHT VERTEX: (5, 4) DIRECTION:

DETERMINE WHICH WAY THE PARABOLA OPENS AND WHERE THE VERTEX IS. OPENS: UP VERTEX: OPENS: RIGHT VERTEX: OPENS: LEFT VERTEX: OPENS: UP OPENS: RIGHT VERTEX: OPENS: DOWN VERTEX:

WARM UP DETERMINE WHICH WAY THE PARABOLA OPENS AND FIND THE VERTEX. Direction: Vertex:

Objectives WRITE THE STANDARD EQUATION OF A PARABOLA AND ITS AXIS OF SYMMETRY. GRAPH A PARABOLA AND IDENTIFY ITS FOCUS, DIRECTRIX, AND AXIS OF SYMMETRY.

Vocabulary FOCUS OF A PARABOLA DIRECTRIX

In Chapter 5, you learned that the graph of a quadratic function is a parabola. Because a parabola is a conic section, it can also be defined in terms of distance.

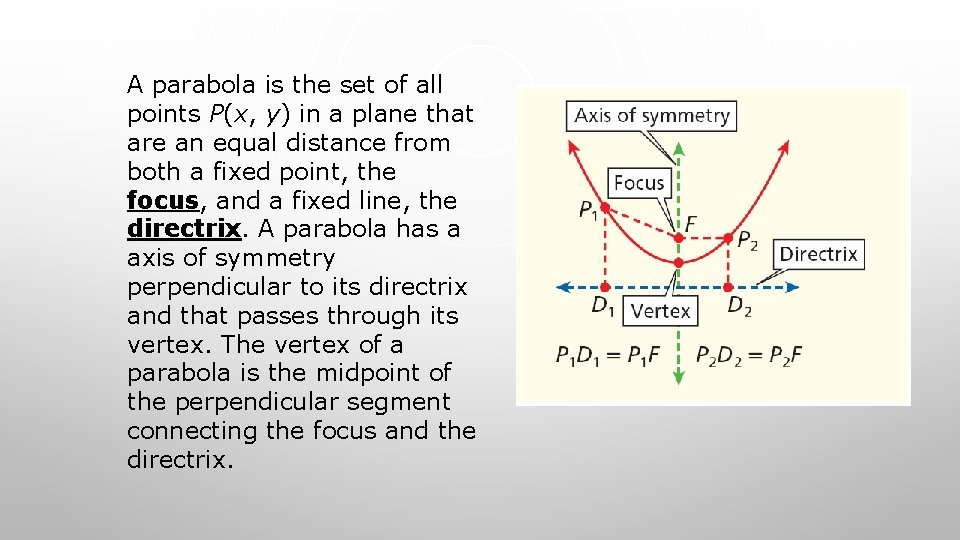
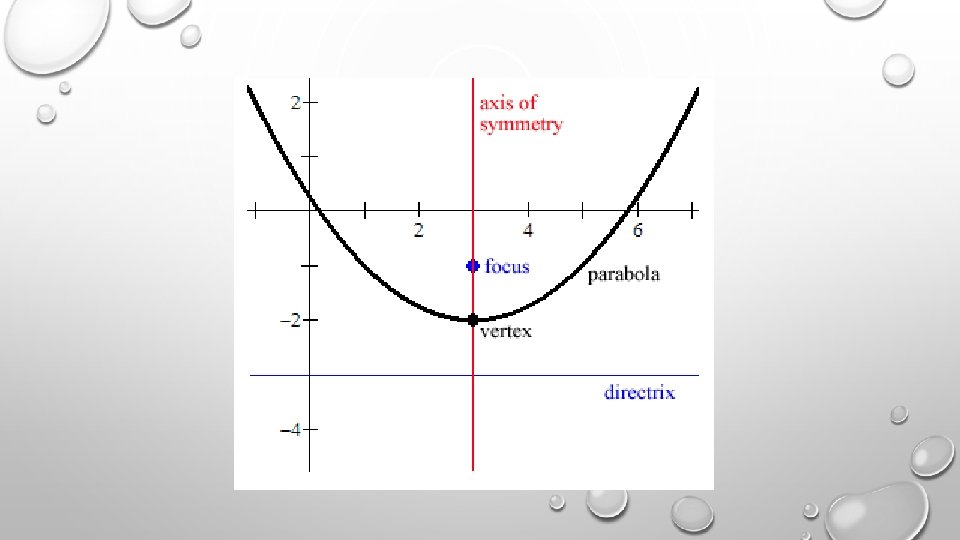
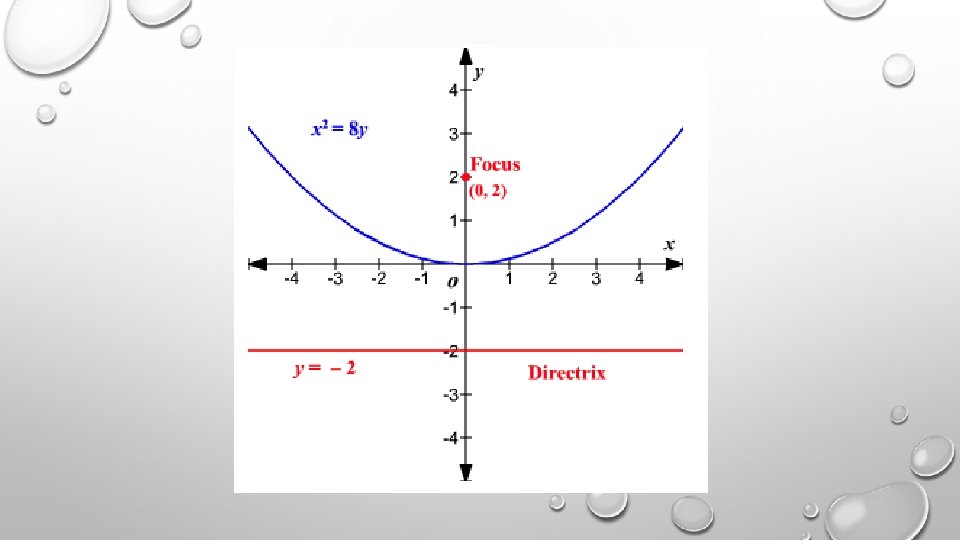
A parabola is the set of all points P(x, y) in a plane that are an equal distance from both a fixed point, the focus, and a fixed line, the directrix. A parabola has a axis of symmetry perpendicular to its directrix and that passes through its vertex. The vertex of a parabola is the midpoint of the perpendicular segment connecting the focus and the directrix.

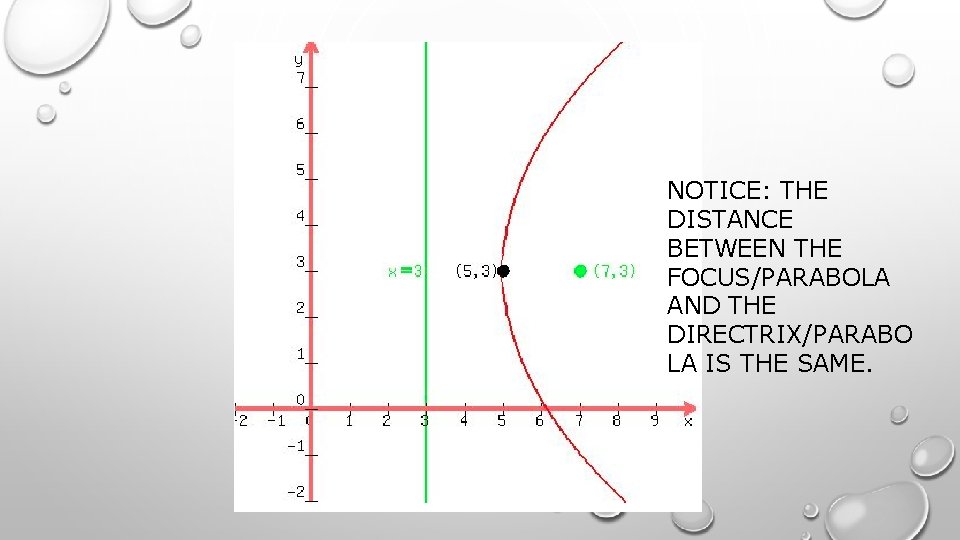
Remember! The distance from a point to a line is defined as the length of the line segment from the point perpendicular to the line.

NOTICE: THE DISTANCE BETWEEN THE FOCUS/PARABOLA AND THE DIRECTRIX/PARABO LA IS THE SAME.

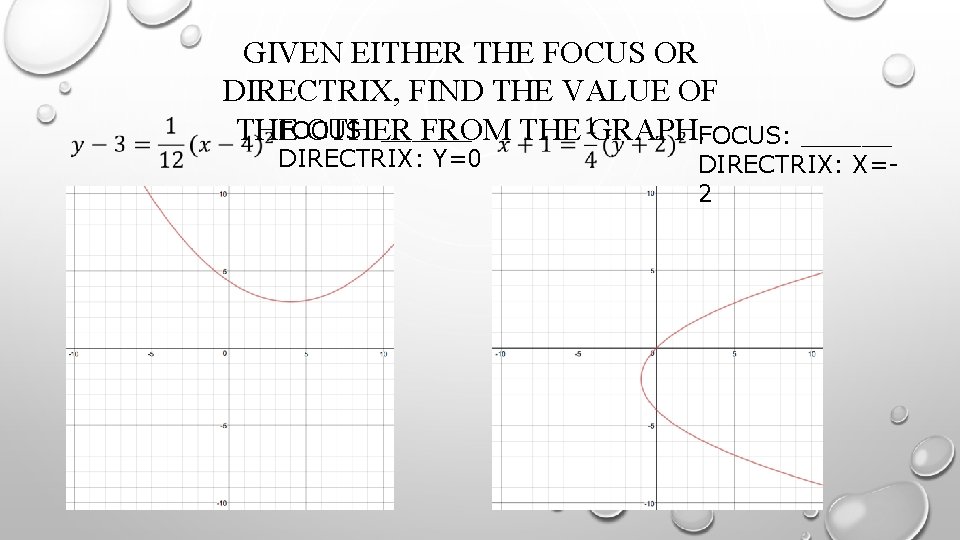
GIVEN EITHER THE FOCUS OR DIRECTRIX, FIND THE VALUE OF THE OTHER FROM THE GRAPH. FOCUS: (0, 2) FOCUS: (4, 0) DIRECTRIX: ______

GIVEN EITHER THE FOCUS OR DIRECTRIX, FIND THE VALUE OF FOCUS: ______ THE OTHER FROM THE GRAPH. FOCUS: ______ DIRECTRIX: Y=0 DIRECTRIX: X=2

Example 1: Using the Distance Formula to Write the Equation of a Parabola Use the Distance Formula to find the equation of a parabola with focus F(2, 4) and directrix y = – 4. PF = PD Definition of a parabola. Distance Formula. Substitute (2, 4) for (x 1, y 1) and (x, – 4) for (x 2, y 2).

Example 1 Continued Simplify. (x – 2)2 + (y – 4)2 = (y + 4)2 Square both sides. (x – 2)2 + y 2 – 8 y + 16 = y 2 + 8 y + 16 Expand. 2 Subtract y and 16 2 (x – 2) – 8 y = 8 y from both sides. (x – 2)2 = 16 y Add 8 y to both sides. Solve for y.

Example 2 Use the Distance Formula to find the equation of a parabola with focus F(0, 4) and directrix y = – 4. PF = PD Definition of a parabola. Distance Formula Substitute (0, 4) for (x 1, y 1) and (x, – 4) for (x 2, y 2).

Check It Out! Example 1 Continued Simplify. x 2 + (y – 4)2 = (y + 4)2 Square both sides. x 2 + y 2 – 8 y + 16 = y 2 + 8 y +16 Expand. 2 x – 8 y = 8 y x 2 = 16 y Subtract y 2 and 16 from both sides. Add 8 y to both sides. Solve for y.

Previously, you have graphed parabolas with vertical axes of symmetry that open upward or downward. Parabolas may also have horizontal axes of symmetry and may open to the left or right. The equations of parabolas use the parameter p. The |p| gives the distance from the vertex to both the focus and the directrix.

Example 3: Writing Equations of Parabolas Write the equation in standard form for the parabola. Step 1 Because the axis of symmetry is vertical and the parabola opens downward, the equation is in the form y= 1 4 p x 2 with p < 0.

Example 3 Continued Step 2 The distance from the focus (0, – 5) to the vertex (0, 0), is 5, so p = – 5 and 4 p = – 20. Step 3 The equation of the parabola is y = – Check Use your graphing calculator. The graph of the equation appears to match. 1 20 x 2.

Example 4: Writing Equations of Parabolas Write the equation in standard form for the parabola. vertex (0, 0), directrix x = – 6 Step 1 Because the directrix is a vertical line, the equation is in the form . The vertex is to the right of the directrix, so the graph will open to the right.

Example 4 Continued Step 2 Because the directrix is x = – 6, p = 6 and 4 p = 24. Step 3 The equation of the parabola is x = Check Use your graphing calculator. 1 24 y. 2

Example 5 Write the equation in standard form for the parabola. vertex (0, 0), directrix x = 1. 25 Step 1 Because the directrix is a vertical line, the equation is in the form of . The vertex is to the left of the directrix, so the graph will open to the left.

Example 5 Continued Step 2 Because the directrix is x = 1. 25, p = – 1. 25 and 4 p = – 5. Step 3 The equation of the parabola is Check Use your graphing calculator.

The vertex of a parabola may not always be the origin. Adding or subtracting a value from x or y translates the graph of a parabola. Also notice that the values of p stretch or compress the graph.

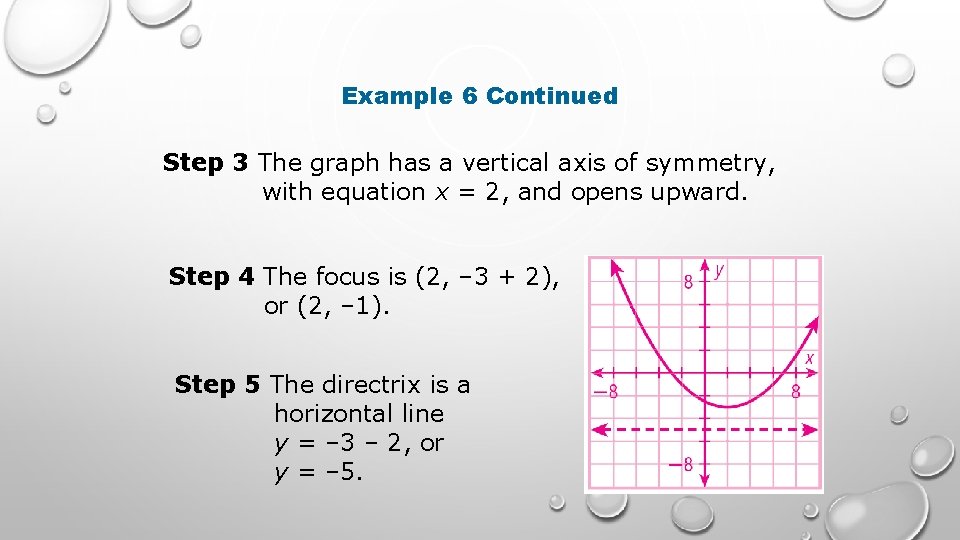
Example 6: Graphing Parabolas Find the vertex, value of p, axis of symmetry, focus, and directrix of the parabola y + 3 = 1 (x – 2)2. Then graph. 8 Step 1 The vertex is (2, – 3). Step 2 1 4 p = 1 , so 4 p = 8 and p = 2. 8

Example 6 Continued Step 3 The graph has a vertical axis of symmetry, with equation x = 2, and opens upward. Step 4 The focus is (2, – 3 + 2), or (2, – 1). Step 5 The directrix is a horizontal line y = – 3 – 2, or y = – 5.

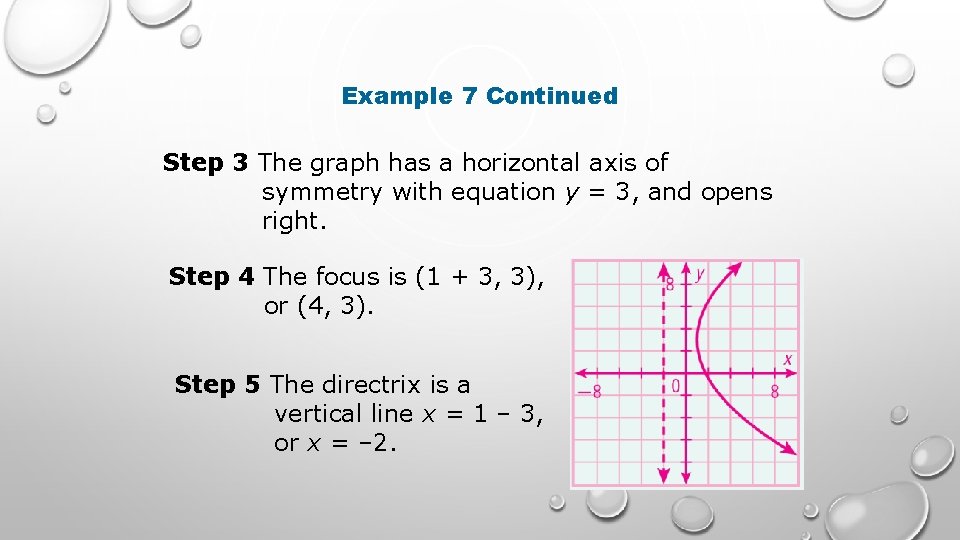
Example 7 Find the vertex, value of p, axis of symmetry, focus, and directrix of the parabola. Then graph. Step 1 The vertex is (1, 3). Step 2 1 4 p = 1 , so 4 p = 12 and p = 3. 12

Example 7 Continued Step 3 The graph has a horizontal axis of symmetry with equation y = 3, and opens right. Step 4 The focus is (1 + 3, 3), or (4, 3). Step 5 The directrix is a vertical line x = 1 – 3, or x = – 2.

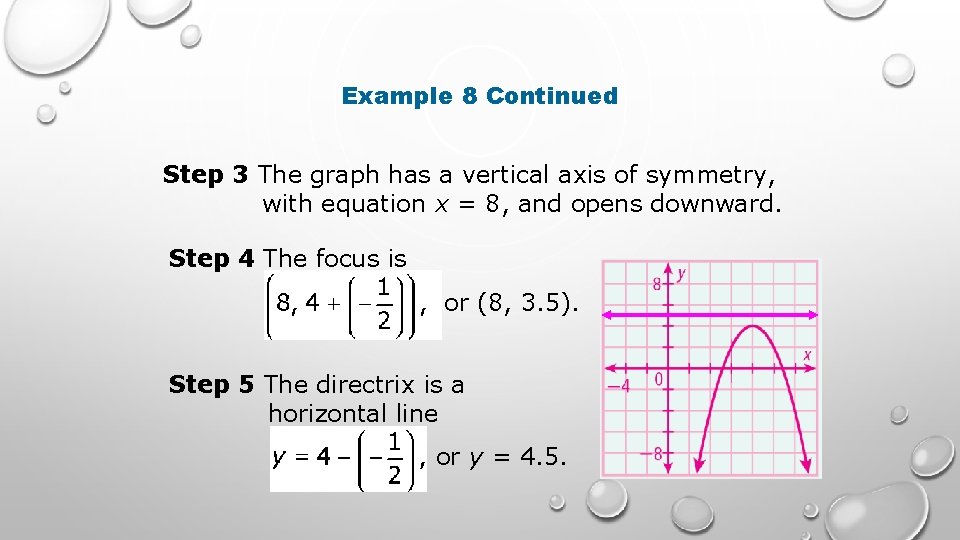
Example 8 Find the vertex, value of p axis of symmetry, focus, and directrix of the parabola. Then graph. Step 1 The vertex is (8, 4). Step 2 1 4 p 1 = – 1 , so 4 p = – 2 and p = –. 2 2

Example 8 Continued Step 3 The graph has a vertical axis of symmetry, with equation x = 8, and opens downward. Step 4 The focus is or (8, 3. 5). Step 5 The directrix is a horizontal line or y = 4. 5.

Light or sound waves collected by a parabola will be reflected by the curve through the focus of the parabola, as shown in the figure. Waves emitted from the focus will be reflected out parallel to the axis of symmetry of a parabola. This property is used in communications technology.

Example 4: Using the Equation of a Parabola The cross section of a larger parabolic microphone can be modeled by the equation 1 2 What is the length yof x=. the feedhorn? 132 The equation for the cross section is in the form x= 1 4 p y 2, so 4 p = 132 and p = 33. The focus should be 33 inches from the vertex of the cross section. Therefore, the feedhorn should be 33 inches long.

Check It Out! Example 4 Find the length of the feedhorn for a microphone with a cross section equation x = 1 y 2. 44 The equation for the cross section is in the form x= 1 4 p y 2, so 4 p = 44 and p = 11. The focus should be 11 inches from the vertex of the cross section. Therefore, the feedhorn should be 11 inches long.

Lesson Quiz 1. Write an equation for the parabola with focus F(0, 0) and directrix y = 1. 2. Find the vertex, value of p, axis of symmetry, focus, 1 and directrix of the parabola y – 2 = (x – 4)2, 12 then graph. vertex: (4, 2); focus: (4, 5); directrix: y = – 1; p = 3; axis of symmetry: x = 4