Variants of HMMs Higherorder HMMs How do we

Variants of HMMs

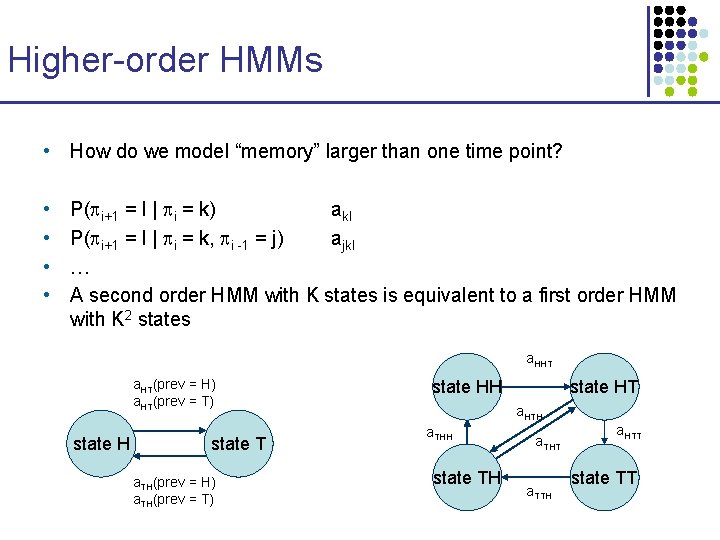
Higher-order HMMs • How do we model “memory” larger than one time point? • • P( i+1 = l | i = k) akl P( i+1 = l | i = k, i -1 = j) ajkl … A second order HMM with K states is equivalent to a first order HMM with K 2 states a. HHT a. HT(prev = H) a. HT(prev = T) state H state T a. TH(prev = H) a. TH(prev = T) state HH state HT a. HTH a. THH state TH a. THT a. TTH a. HTT state TT

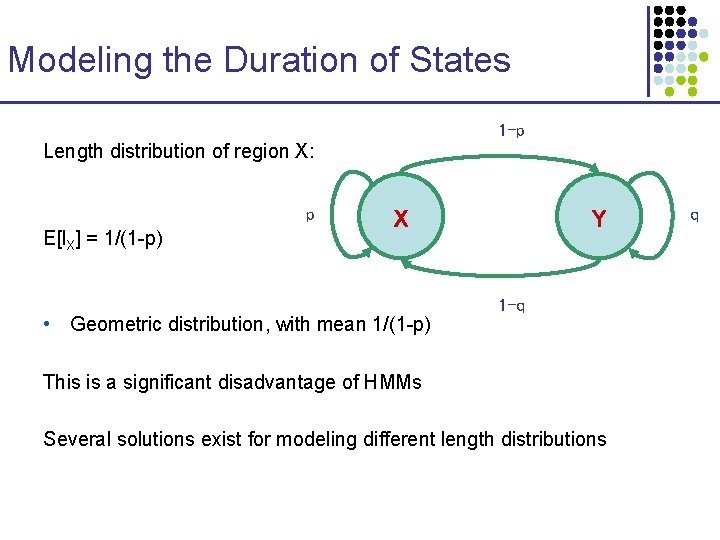
Modeling the Duration of States 1 -p Length distribution of region X: p E[l. X] = 1/(1 -p) X • Geometric distribution, with mean 1/(1 -p) Y 1 -q This is a significant disadvantage of HMMs Several solutions exist for modeling different length distributions q

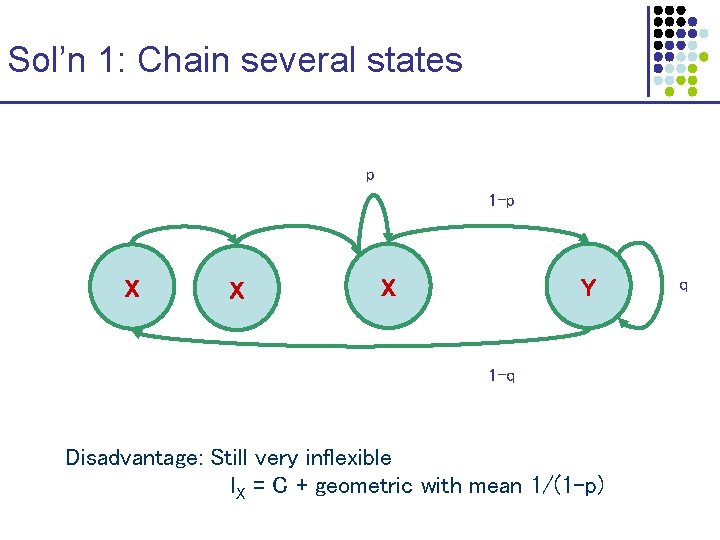
Sol’n 1: Chain several states p 1 -p X X X Y 1 -q Disadvantage: Still very inflexible l. X = C + geometric with mean 1/(1 -p) q

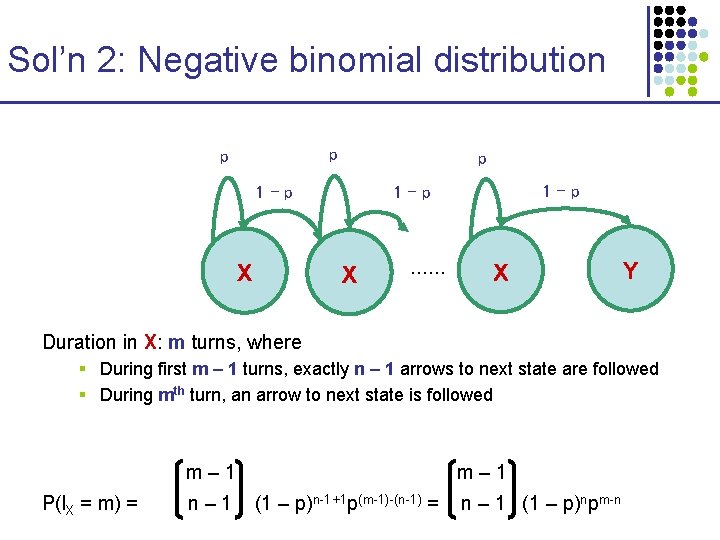
Sol’n 2: Negative binomial distribution p p p 1–p X …… X Y Duration in X: m turns, where § During first m – 1 turns, exactly n – 1 arrows to next state are followed § During mth turn, an arrow to next state is followed m– 1 P(l. X = m) = n– 1 m– 1 (1 – p)n-1+1 p(m-1)-(n-1) = n – 1 (1 – p)npm-n

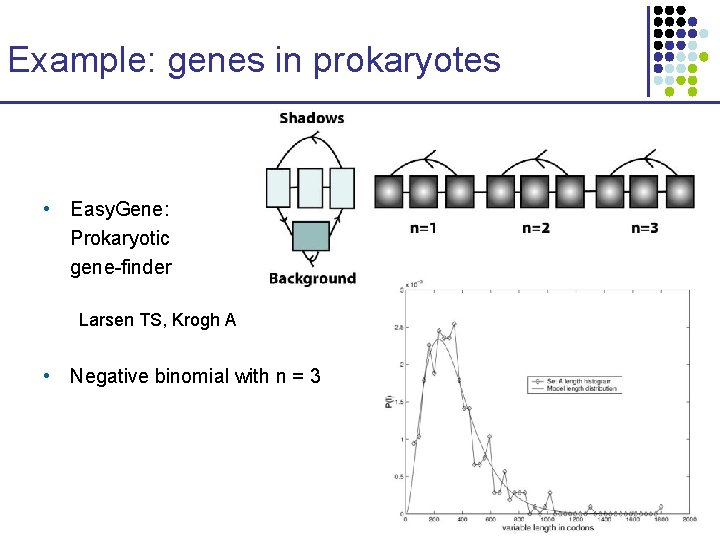
Example: genes in prokaryotes • Easy. Gene: Prokaryotic gene-finder Larsen TS, Krogh A • Negative binomial with n = 3

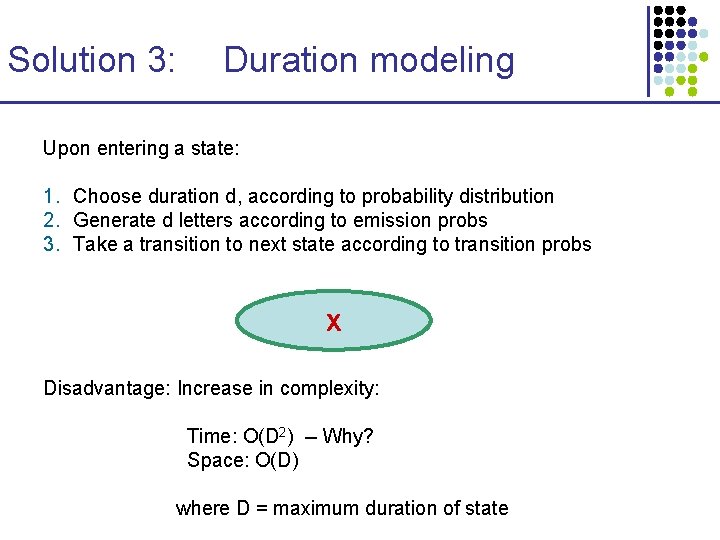
Solution 3: Duration modeling Upon entering a state: 1. Choose duration d, according to probability distribution 2. Generate d letters according to emission probs 3. Take a transition to next state according to transition probs X Disadvantage: Increase in complexity: Time: O(D 2) -- Why? Space: O(D) where D = maximum duration of state

Connection Between Alignment and HMMs

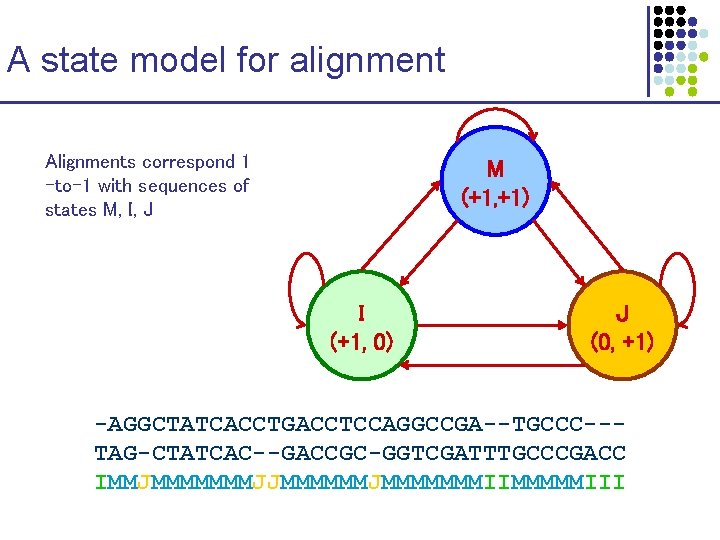
A state model for alignment Alignments correspond 1 -to-1 with sequences of states M, I, J M (+1, +1) I (+1, 0) J (0, +1) -AGGCTATCACCTGACCTCCAGGCCGA--TGCCC--TAG-CTATCAC--GACCGC-GGTCGATTTGCCCGACC IMMJMMMMMMMJJMMMMMMMIIMMMMMIII

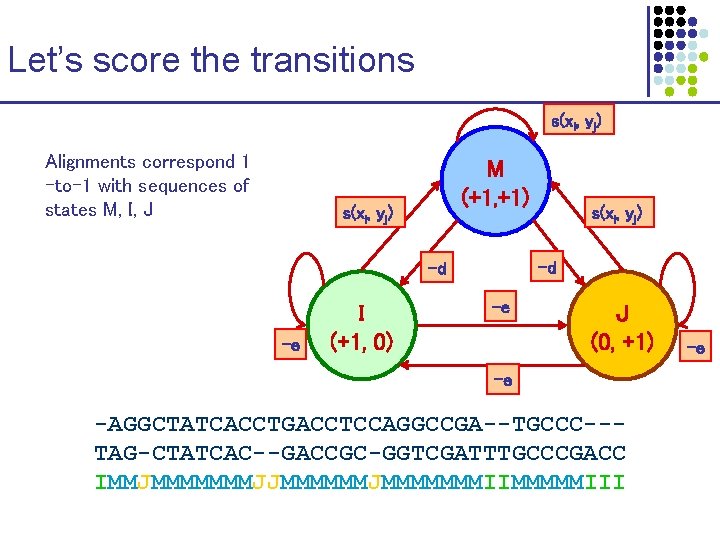
Let’s score the transitions s(xi, yj) Alignments correspond 1 -to-1 with sequences of states M, I, J M (+1, +1) s(xi, yj) -d -d -e I (+1, 0) s(xi, yj) -e J (0, +1) -e -AGGCTATCACCTGACCTCCAGGCCGA--TGCCC--TAG-CTATCAC--GACCGC-GGTCGATTTGCCCGACC IMMJMMMMMMMJJMMMMMMMIIMMMMMIII -e

How do we find optimal alignment according to this model? Dynamic Programming: M(i, j): Optimal alignment of x 1…xi to y 1…yj ending in M I(i, j): Optimal alignment of x 1…xi to y 1…yj ending in I J(i, j): Optimal alignment of x 1…xi to y 1…yj ending in J The score is additive, therefore we can apply DP recurrence formulas

Needleman Wunsch with affine gaps – state version Initialization: M(0, 0) = 0; M(i, 0) = M(0, j) = - , for i, j > 0 I(i, 0) = d + i e; J(0, j) = d + j e Iteration: M(i, j) = s(xi, yj) + max M(i – 1, j – 1) I(i – 1, j – 1) J(i – 1, j – 1) I(i, j) = max e + I(i – 1, j) e + J(i, j – 1) d + M(i – 1, j – 1) J(i, j) = Termination: Optimal alignment given by max { M(m, n), I(m, n), J(m, n) }

Probabilistic interpretation of an alignment An alignment is a hypothesis that the two sequences are related by evolution Goal: Produce the most likely alignment Assert the likelihood that the sequences are indeed related

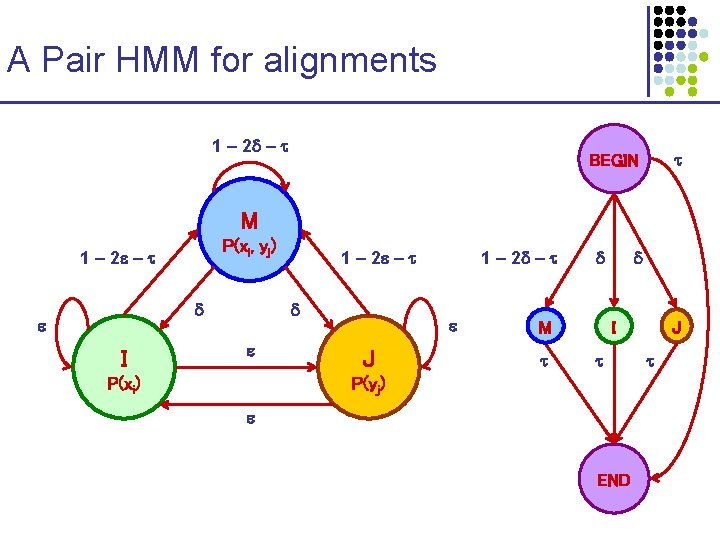
A Pair HMM for alignments 1 – 2 – BEGIN M P(xi, yj) 1 – 2 – I P(xi) 1 – 2 – J M I P(yj) END J

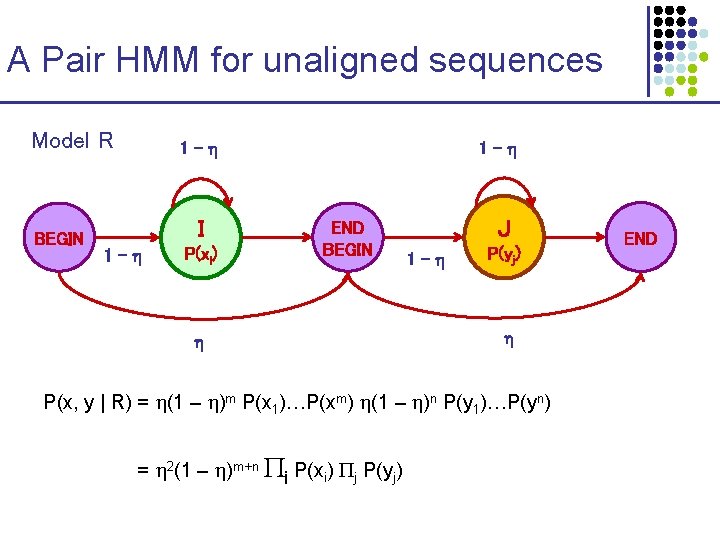
A Pair HMM for unaligned sequences Model R BEGIN 1 - I 1 - P(xi) 1 - END BEGIN J 1 - P(yj) P(x, y | R) = (1 – )m P(x 1)…P(xm) (1 – )n P(y 1)…P(yn) = 2(1 – )m+n i P(xi) j P(yj) END

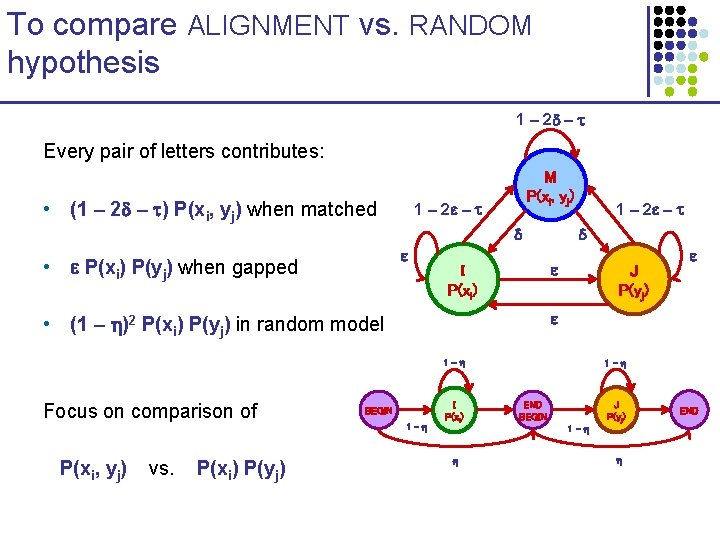
To compare ALIGNMENT vs. RANDOM hypothesis 1 – 2 – Every pair of letters contributes: • (1 – 2 – ) P(xi, yj) when matched 1 – 2 – • P(xi) P(yj) when gapped M P(xi, yj) 1 – 2 – I P(xi) J P(yj) • (1 – )2 P(xi) P(yj) in random model 1 - Focus on comparison of P(xi, yj) vs. P(xi) P(yj) BEGIN 1 - I P(xi) 1 - END BEGIN 1 - J P(yj) END

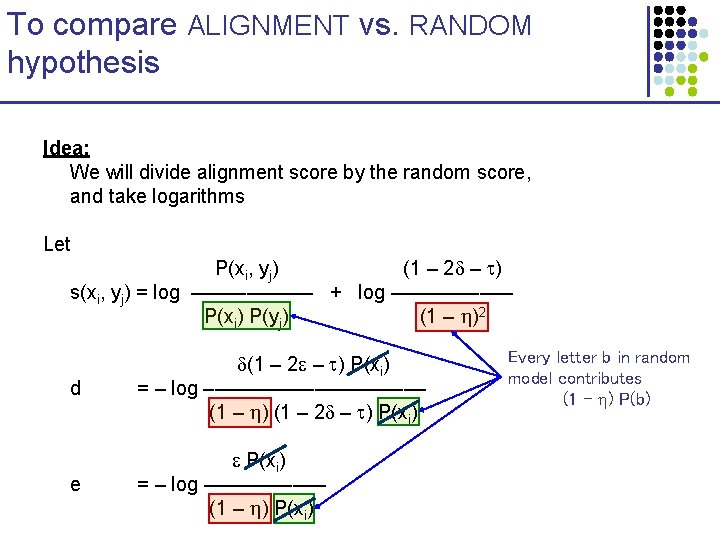
To compare ALIGNMENT vs. RANDOM hypothesis Idea: We will divide alignment score by the random score, and take logarithms Let P(xi, yj) (1 – 2 – ) s(xi, yj) = log –––––– + log –––––– P(xi) P(yj) (1 – )2 d (1 – 2 – ) P(xi) = – log –––––––––– (1 – ) (1 – 2 – ) P(xi) e P(xi) = – log –––––– (1 – ) P(xi) Every letter b in random model contributes (1 – ) P(b)

The meaning of alignment scores • The Viterbi algorithm for Pair HMMs corresponds exactly to the Needleman-Wunsch algorithm with affine gaps • However, now we need to score alignment with parameters that add up to probability distributions § § 1/mean length of next gap 1/mean arrival time of next gap § affine gaps decouple arrival time with length § § 1/mean length of aligned sequences 1/mean length of unaligned sequences (set to ~0)

The meaning of alignment scores Match/mismatch scores: P(xi, yj) s(a, b) log –––––– P(xi) P(yj) (let’s ignore log(1 – 2 ) for the moment – assume no gaps) Example: Say DNA regions between human and mouse have average conservation of 50% Then P(A, A) = P(C, C) = P(G, G) = P(T, T) = 1/8 P(A, C) = P(A, G) =……= P(T, G) = 1/24 (so they sum to ½) (24 mismatches, sum to ½) Say P(A) = P(C) = P(G) = P(T) = ¼ log [ (1/8) / (1/4 * 1/4) ] = log 2 = 1, for match Then, s(a, b) = log [ (1/24) / (1/4 * 1/4) ] = log 16/24 = -0. 585 Cutoff similarity that scores 0: s*1 – (1 – s)*0. 585 = 0 According to this model, a 37. 5%-conserved sequence with no gaps would score on average 0. 375 * 1 – 0. 725 * 0. 585 = 0 Why? 37. 5% is between the 50% conservation model, and the random 25% conservation model !

Substitution matrices A more meaningful way to assign match/mismatch scores For protein sequences, different substitutions have dramatically different frequencies! PAM Matrices: 1. Start from a curated set of very similar protein sequences 2. Construct ancestral sequences (using parsimony) 3. Calculate Aab: frequency of letters a and b interchanging 4. 5. Calculate Bab = P(b|a) = Aab/( c≤d Acd) Adjust matrix B so that a, b qa qb Bab = 0. 01 6. Let PAM(N) = [PAM(1)]N -- PAM(1) Common PAM(250)

Substitution Matrices BLOSUM matrices: 1. 2. 3. Start from BLOCKS database (curated, gap-free alignments) Cluster sequences according to > X% identity Calculate Aab: # of aligned a-b in distinct clusters, correcting by 1/mn, where m, n are the two cluster sizes 4. Estimate P(a) = ( b Aab)/( c≤d Acd); P(a, b) = Aab/( c≤d Acd)

BLOSUM matrices BLOSUM 50 BLOSUM 62 (The two are scaled differently)