HigherOrder Derivatives Position Velocity Acceleration HigherOrder Derivatives Notation

Higher-Order Derivatives Position, Velocity, & Acceleration

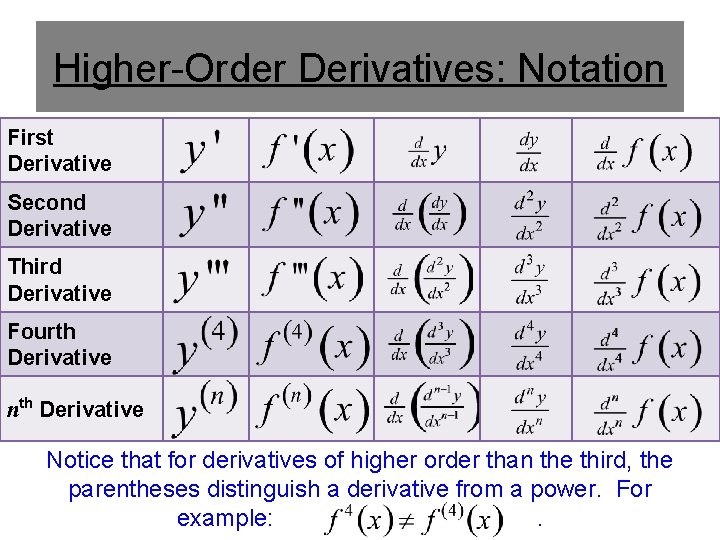
Higher-Order Derivatives: Notation First Derivative Second Derivative Third Derivative Fourth Derivative nth Derivative Notice that for derivatives of higher order than the third, the parentheses distinguish a derivative from a power. For example: .

Example 1 (Continued) Let f. Define the derivatives from (a-e) with the correct notation. You should note that all higher-order derivatives of a polynomial p(x) will also be polynomials, and if p has degree n, then p(n)(x) = 0 for k ≥ n+1.

Example 2 If , find . Will ever equal 0? Find the first derivative: Find the second derivative: Find the third derivative: No higher-order derivative will equal 0 since the power of the function will never be 0. It decreases by one each time.

Example 3 Find the second derivative of Find the first derivative: . Find the second derivative:

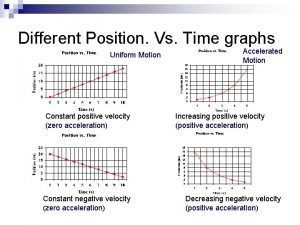
Graphs of a Function and its Derivatives What can we say about g, g'' for the segment of the graph of y = g(x)? As the graph increases, the tangent lines are getting steeper. g : Increasing g' : Positive, Increasing g'' : Positive Since the first derivative is increasing, the second derivative must be positive.

Graphs of a Function and its Derivatives What can we say about g, g'' for the segment of the graph of y = g(x)? As the graph decreases, the tangent lines are getting less steep. g : Decreasing g' : Negative, Decreasing g'' : Negative Since the first derivative is decreasing, the second derivative must be negative.

Graphs of a Function and its Derivatives What can we say about g, g'' for the segment of the graph of y = g(x)? g : Decreasing As the graph decreases, the tangent lines are steeper. g' : Negative, Increasing g'' : Positive Since the first derivative is increasing, the second derivative must be positive.

Graphs of a Function and its Derivatives What can we say about g, g'' for the segment of the graph of y = g(x)? g : Increasing As the graph increases, the tangent lines are getting less steep. g' : Positive, Decreasing g'' : Negative Since the first derivative is decreasing, the second derivative must be negative.

Graphs of a Function and its Derivatives What can we say about g, g'' for the segment of the graph of y = g(x)? On the left side : g : Decreasing g' : Negative, Decreasing g'' : Negative Find the pieces of this graph that compare to the previous graphs. On the right side : g : Decreasing g' : Negative, Increasing g'' : Positive

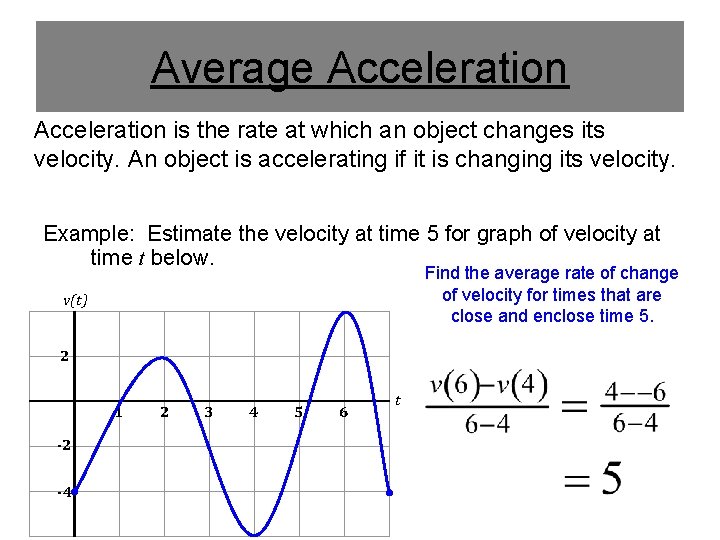
Average Acceleration is the rate at which an object changes its velocity. An object is accelerating if it is changing its velocity. Example: Estimate the velocity at time 5 for graph of velocity at time t below. Find the average rate of change of velocity for times that are close and enclose time 5. v(t) 2 1 -2 -4 2 3 4 5 6 t

Instantaneous Acceleration If s = s(t) is the position function of an object that moves in a straight line, we know that its first derivative represents the velocity v(t) of the object as a function of time. The instantaneous rate of change of velocity with respect to time is called the acceleration a(t) of an object. Thus, the acceleration function is the derivative of the velocity function and is therefore the second derivative of the position function.

Position, Velocity, and Acceleration are related in the following manner: Position: Velocity: Units = Measure of length (ft, m, km, etc) The object is… Moving right/up when v(t) > 0 Moving left/down when v(t) < 0 Still or changing directions when v(t) = 0 Units = Distance/Time (mph, m/s, ft/hr, etc) Speed = absolute value of v(t) Acceleration: Units = (Distance/Time)/Time (m/s 2)

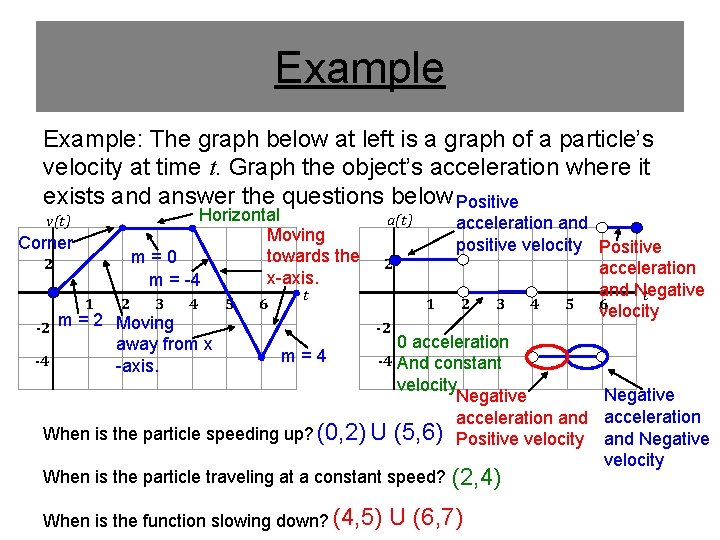
Example: The graph below at left is a graph of a particle’s velocity at time t. Graph the object’s acceleration where it exists and answer the questions below Positive Horizontal Moving towards the m=0 x-axis. m = -4 v(t) Corner 2 1 2 3 -2 m = 2 Moving 4 5 6 a(t) 2 t 1 -2 acceleration and positive velocity Positive acceleration and Negative t 2 3 4 5 6 velocity 0 acceleration m=4 -4 And constant -4 velocity Negative acceleration and acceleration When is the particle speeding up? (0, 2) U (5, 6) Positive velocity and Negative velocity When is the particle traveling at a constant speed? (2, 4) away from x -axis. When is the function slowing down? (4, 5) U (6, 7)

Speeding Up and Slowing Down An object is SPEEDING UP when the following occur: • Algebraic: If the velocity and the acceleration agree in sign • Graphical: If the velocitycurve is moving AWAY from the x-axis An object is traveling at a CONSTANT SPEED when the following occur: • Algebraic: Velocity is constant and acceleration is 0. • Graphically: The velocity curve is horizontal An object is SLOWING DOWN when the following occur: • Algebraic: Velocity and acceleration disagree in sign • Graphically: The velocity curve is moving towards the x-axis

Example 3 The position of a particle is given by the equation where t is measured in seconds and s in meters. (a) Find the acceleration at time t. The derivative of the velocity function is the acceleration function.

The position of a particle is given by the equation where t is measured in seconds and s in meters. (b) What is the acceleration after 4 seconds? (c) Is the particle speeding up, slowing down, or traveling at a constant speed at 4 seconds? Since the velocity and acceleration agree in signs, the particle is speeding up.

The position of a particle is given by the equation where t is measured in seconds and s in meters. (d) When is the particle speeding up? When is it slowing down?