Chapter 3 Accelerated Motion In this chapter you

Chapter 3 Accelerated Motion In this chapter you will: Develop descriptions of accelerated motions. Use graphs and equations to solve problems involving moving objects. Describe the motion of objects in free fall.

Chapter Table of Contents 3 Chapter 3: Accelerated Motion Section 3. 1: Acceleration Section 3. 2: Motion with Constant Acceleration Section 3. 3: Free Fall Homework Read Chapter 3. Complete Study Guide. Graphical Analysis Packet HW 3: handout

Section 3. 1 Warmup: Which Velocity Is It? Physics Daily Warmup # 16 There are two types of velocity that we encounter in our everyday lives. Instantaneous velocity refers to how fast something is moving at a particular point in time, while average velocity refers to the average speed something travels over a given period of time. For each use of velocity described below, identify whether it is instantaneous velocity or average velocity. 1. The speedometer on your car indicates you are going 65 mph. instantaneous 2. A race-car driver was listed as driving 120 mph for the entire race. average 3. A freely falling object has a speed of 19. 6 m/s after 2 seconds of fall in a vacuum. instantaneous 4. instantaneous The speed limit sign says 45 mph.

Section 3. 1 Acceleration In this section you will: Define acceleration. Relate velocity and acceleration to the motion of an object. Create velocity-time graphs.

Section Acceleration 3. 1 Changing Velocity You can feel a difference between uniform and nonuniform motion. When you move in nonuniform motion, you feel pushed or pulled. In contrast, when you are in uniform motion and your eyes are closed, you feel as though you are not moving at all.

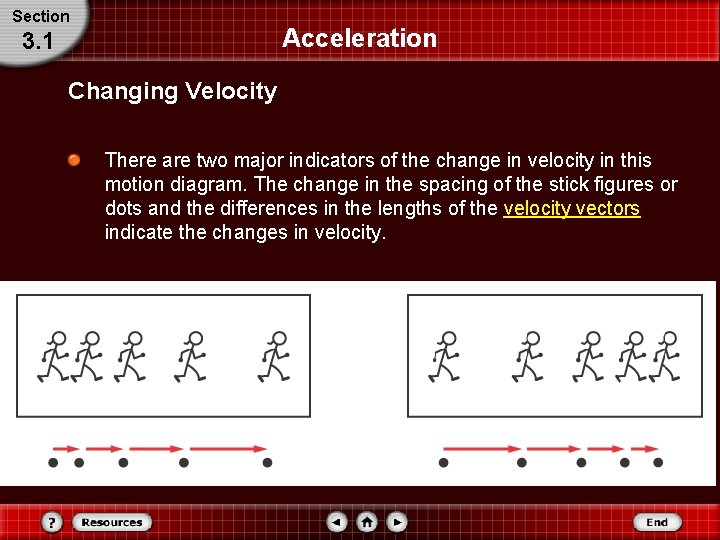
Section Acceleration 3. 1 Changing Velocity Consider the motion diagrams below showing the distance between successive positions.

Section Acceleration 3. 1 Changing Velocity There are two major indicators of the change in velocity in this motion diagram. The change in the spacing of the stick figures or dots and the differences in the lengths of the velocity vectors indicate the changes in velocity.

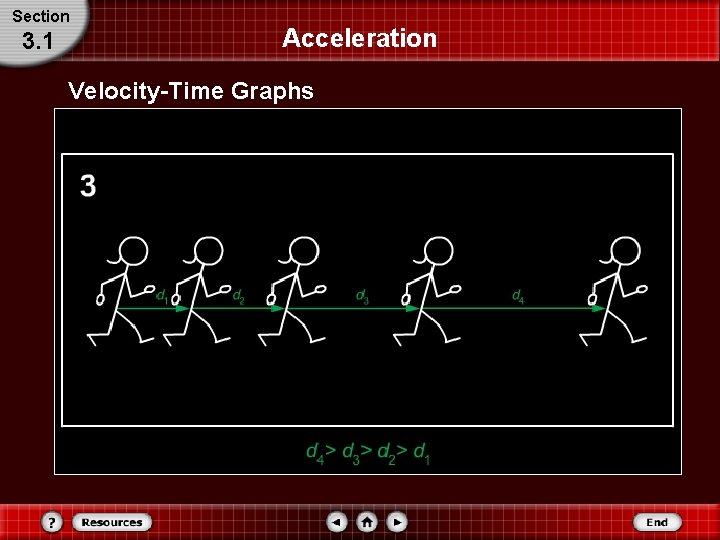
Section Acceleration 3. 1 Changing Velocity If an object speeds up, each subsequent velocity vector is longer. If the object slows down, each vector is shorter than the previous one. Both types of motion diagrams give an idea of how an object’s velocity is changing.

Section 3. 1 Acceleration Velocity-Time Graphs

Section 3. 1 Acceleration Average and Instantaneous Acceleration The rate at which an object’s velocity changes is called the acceleration of the object. When the velocity of an object changes at a constant rate, it has a constant acceleration. The average acceleration of an object is the change in velocity during some measurable time interval divided by that time interval. Average acceleration is measured in m/s 2. The change in velocity at an instant of time is called instantaneous acceleration.

Section 3. 1 Please Do Now Describe the part of a rollercoaster ride that would be uniform motion and the part that would be non-uniform motion. Write (3) lines.

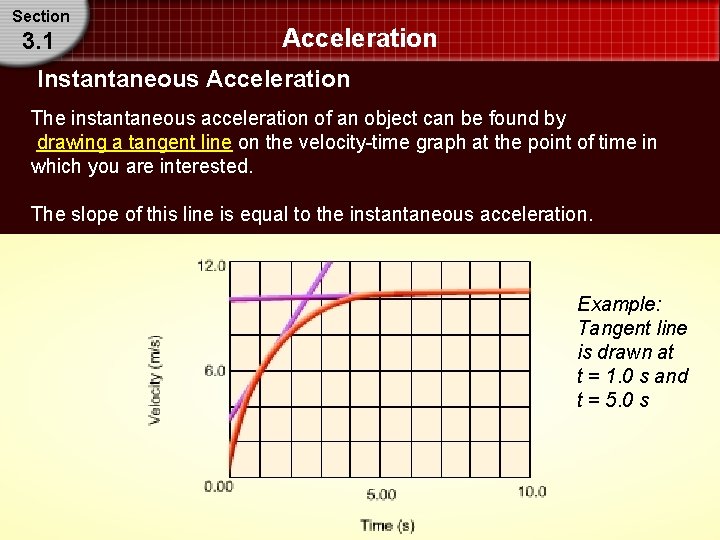
Section 3. 1 Acceleration Instantaneous Acceleration The instantaneous acceleration of an object can be found by drawing a tangent line on the velocity-time graph at the point of time in which you are interested. The slope of this line is equal to the instantaneous acceleration. Example: Tangent line is drawn at t = 1. 0 s and t = 5. 0 s

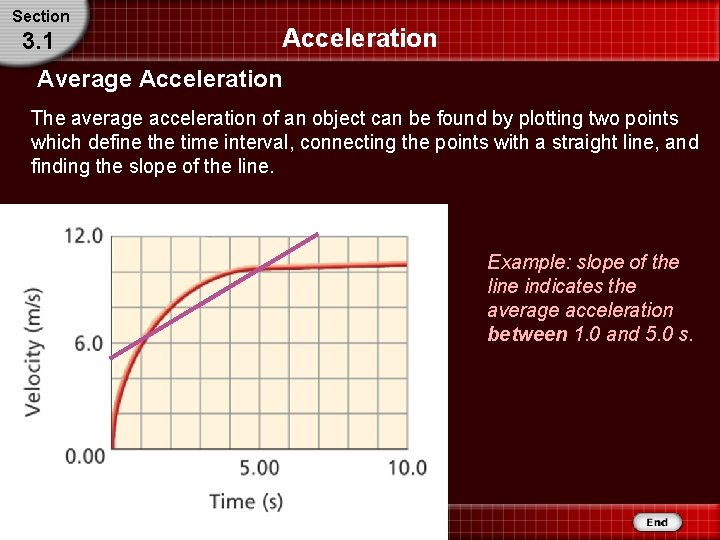
Section 3. 1 Acceleration Average Acceleration The average acceleration of an object can be found by plotting two points which define the time interval, connecting the points with a straight line, and finding the slope of the line. Example: slope of the line indicates the average acceleration between 1. 0 and 5. 0 s.

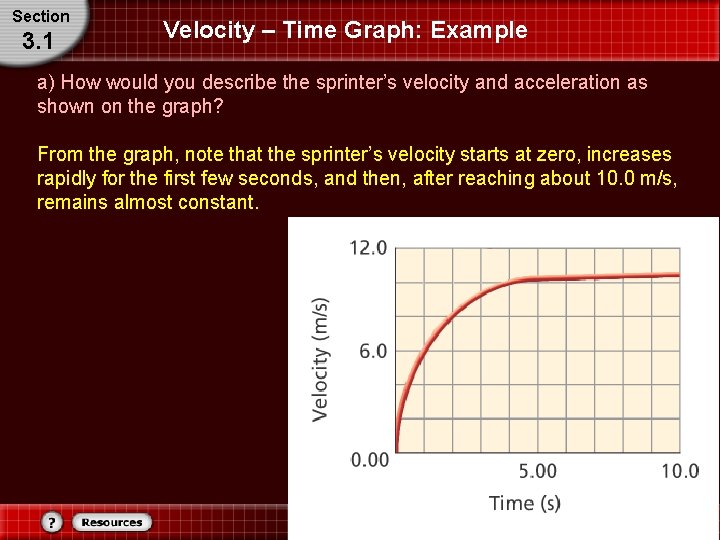
Section 3. 1 Velocity – Time Graph: Example a) How would you describe the sprinter’s velocity and acceleration as shown on the graph? From the graph, note that the sprinter’s velocity starts at zero, increases rapidly for the first few seconds, and then, after reaching about 10. 0 m/s, remains almost constant.

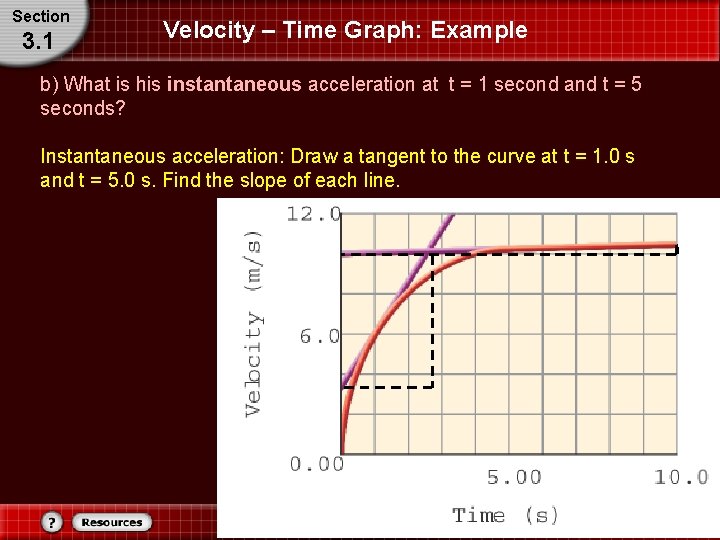
Section 3. 1 Velocity – Time Graph: Example b) What is his instantaneous acceleration at t = 1 second and t = 5 seconds? Instantaneous acceleration: Draw a tangent to the curve at t = 1. 0 s and t = 5. 0 s. Find the slope of each line.

Section 3. 1 Velocity – Time Graph: Example Solve for acceleration at 1. 0 s: Solve for acceleration at 5. 0 s: The acceleration is not constant because it changes from 3. 4 m/s 2 to 0. 03 m/s 2 at 5. 0 s. The acceleration is in the direction chosen to be positive because both values are positive.

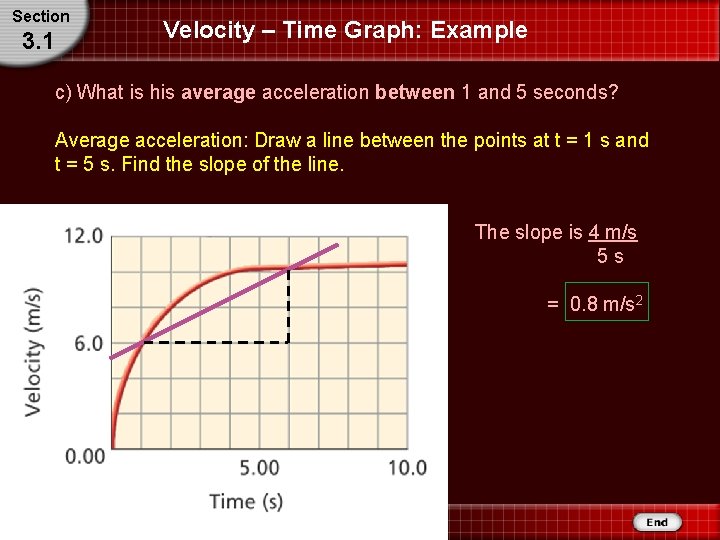
Section 3. 1 Velocity – Time Graph: Example c) What is his average acceleration between 1 and 5 seconds? Average acceleration: Draw a line between the points at t = 1 s and t = 5 s. Find the slope of the line. The slope is 4 m/s 5 s = 0. 8 m/s 2

Section 3. 1 Exit Ticket Write in your own words, what is the difference between velocity and acceleration?

Section Exit Ticket 3. 1 1. Is a ride on an escalator uniform or non-uniform motion? uniform 2. What does the slope of the line on a position-time graph indicate? velocity 3. What does the slope of the line on a velocity-time graph indicate? acceleration

Section 3. 1 Please Do Now Speed is how fast something is moving. Velocity is how fast AND in what direction. Acceleration is speeding up or slowing down AND in what direction. Write 1 -3 sentences using the words speed, velocity, and acceleration. Example: The rocket accelerated off the launch pad, gaining speed with each passing second. It reached a velocity of 25, 000 miles per hour as it left the earths’s atmosphere.

Section 3. 1 Acceleration Positive and Negative Acceleration These four motion diagrams represent the four different possible ways to move along a straight line with constant acceleration. Positive direction, speeding up Positive direction, slowing down Negative direction, speeding up Negative direction, slowing down

Section 3. 1 Acceleration Positive and Negative Acceleration v When the object is speeding up, the velocity and acceleration vectors point in the same direction. (case 1 and 3) a When the object is slowing down, the velocity and acceleration vectors point in opposite directions (case 2 and 4) a Both the direction of an object’s velocity and its direction of acceleration are needed to determine whether it is speeding up or slowing down. v v a

Section 3. 1 Acceleration Positive and Negative Acceleration An object has a positive acceleration when the acceleration vector points in the positive direction and a negative acceleration, when the acceleration vector points in the negative direction. The sign of acceleration does not indicate whether the object is speeding up or slowing down. v +a v -a v +a

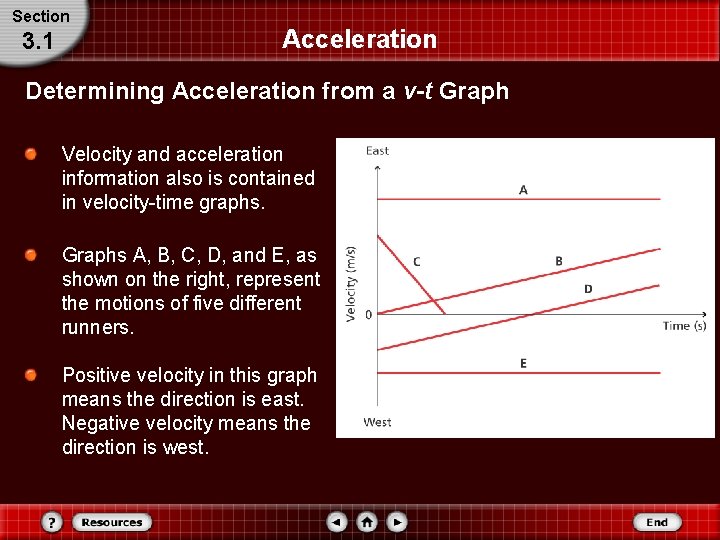
Section 3. 1 Acceleration Determining Acceleration from a v-t Graph Velocity and acceleration information also is contained in velocity-time graphs. Graphs A, B, C, D, and E, as shown on the right, represent the motions of five different runners. Positive velocity in this graph means the direction is east. Negative velocity means the direction is west.

Section 3. 1 Determining Acceleration from a v-t Graph Describe the direction of motion, velocity and acceleration for: Graph A: Zero slope means zero acceleration; constant velocity towards the east. Graph B: Starting with zero velocity, picking up speed, moving towards the east. The straight line indicates constant acceleration. Graph C: Moving towards the east while slowing down and eventually stopping. Slowing down with a constant negative acceleration.

Section 3. 1 Determining Acceleration from a v-t Graph D: Moving towards the west while slowing down, turns around, then moves east while speeding up. Graph E: Moving west with constant velocity, zero acceleration. Remember, for a velocity-time graph: - positive velocity occurs when the line is anywhere above the x-axis - positive velocity means the object is moving in the positive direction, which might be east, to the right, etc. - the slope of the line indicated the acceleration - a straight line means constant acceleration

Section 3. 1 Acceleration Determining Acceleration from a v-t Graph The following equation expresses average acceleration as the slope of the velocity-time graph. Average acceleration is equal to the change in velocity, divided by the time it takes to make that change.

Section 3. 1 Acceleration Example: Suppose you run a wind sprints back and forth across the gym. You run at a speed of 4. 0 m/s toward the wall, touch and run back at the same speed. The whole trip takes 10 seconds. What is your average acceleration if the positive direction is toward the wall? Givens: vi = 4 m/s; vf = -4 m/s; t = 10 s Unknown: a Equation: Substitute and Solve: Sense: The negative sign means the acceleration is away from the wall. Change in direction of motion results in acceleration.

Section Check 3. 1 Question 1 Which of the following statements correctly define acceleration? A. Acceleration is the rate of change of displacement of an object. B. Acceleration is the rate of change of velocity of an object. C. Acceleration is the amount of distance covered in unit time. D. Acceleration is the rate of change of speed of an object.

Section 3. 1 Section Check Answer 1 Answer: B Reason: The rate at which an object’s velocity changes is called acceleration of the object.

Section Check 3. 1 Question 2 What happens when the velocity vector and the acceleration vector of an object in motion are in same direction? A. The acceleration of the object increases. B. The speed of the object increases. C. The object comes to rest. D. The speed of the object decreases.

Section 3. 1 Section Check Answer 2 Answer: B Reason: When the velocity vector and the acceleration vector of an object in motion are in same direction, the speed of the object increases.

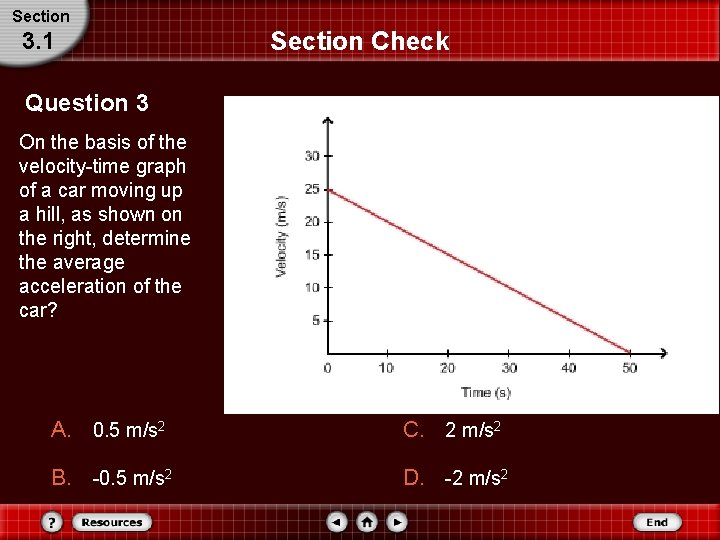
Section 3. 1 Section Check Question 3 On the basis of the velocity-time graph of a car moving up a hill, as shown on the right, determine the average acceleration of the car? A. 0. 5 m/s 2 C. 2 m/s 2 B. -0. 5 m/s 2 D. -2 m/s 2

Section Check 3. 1 Answer 3 Answer: B Reason: Average acceleration of an object is the slope of the velocity-time graph. vf = 0 vi = 25 m/s tf = 50 s ti = 0 a = vf – vi = 0 – 25 m/s tf – ti 50 s - 0 = - 0. 5 m/s 2

Section 3. 2 Please Do Now In full sentences, write (2) things that are the same and (1) thing that is different about velocity and acceleration.

Section 3. 2 Please Do Now Low Road / High Road In full sentences, state which steel ball win the race and explain why. Use the words displacement, velocity and acceleration.

Section 3. 2 3. 1 Practice Problems, p. 64: 6, 7, 9, 10. Motion with Constant Acceleration Low Road / High Road Demo

Section 3. 2 Motion with Constant Acceleration In this section you will: Interpret position-time graphs for motion with constant acceleration. Determine mathematical relationships among position, velocity, acceleration, and time. Apply graphical and mathematical relationships to solve problems related to constant acceleration.

Section 3. 2 Motion with Constant Acceleration Velocity with Average Acceleration If an object’s average acceleration during a time interval is known, then it can be used to determine how much the velocity changed during that time. The definition of average acceleration: can be rewritten as follows:

Section 3. 2 Motion with Constant Acceleration Velocity with Average Acceleration The equation for final velocity with average acceleration can be written as follows: The final velocity is equal to the initial velocity plus the product of the average acceleration and time interval. vi

Section 3. 2 Motion with Constant Acceleration Velocity with Average Acceleration In cases in which the acceleration is constant, the average acceleration, ā, is the same as the instantaneous acceleration, a. The equation for final velocity can be rearranged to find the time at which an object with constant acceleration has a given velocity. It also can be used to calculate the initial velocity of an object when both the velocity and the time at which it occurred are given.

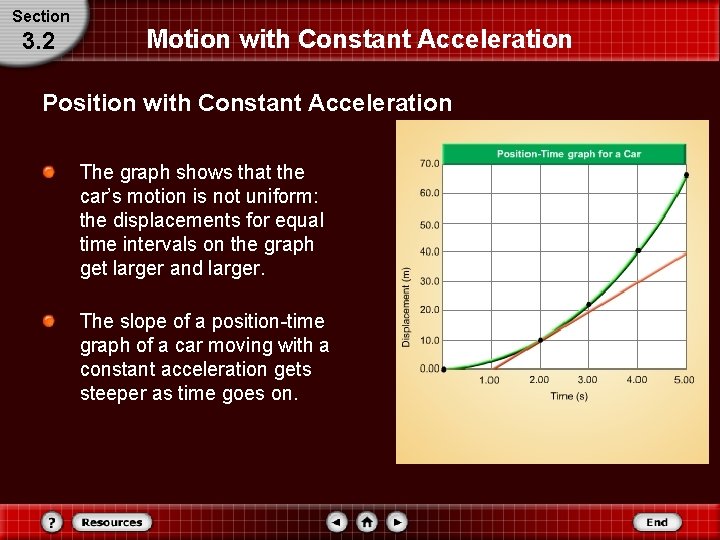
Section 3. 2 Motion with Constant Acceleration Position with Constant Acceleration The position data at different time intervals for a car with constant acceleration are shown in the table. The data from the table are graphed as shown on the next slide.

Section 3. 2 Motion with Constant Acceleration Position with Constant Acceleration The graph shows that the car’s motion is not uniform: the displacements for equal time intervals on the graph get larger and larger. The slope of a position-time graph of a car moving with a constant acceleration gets steeper as time goes on.

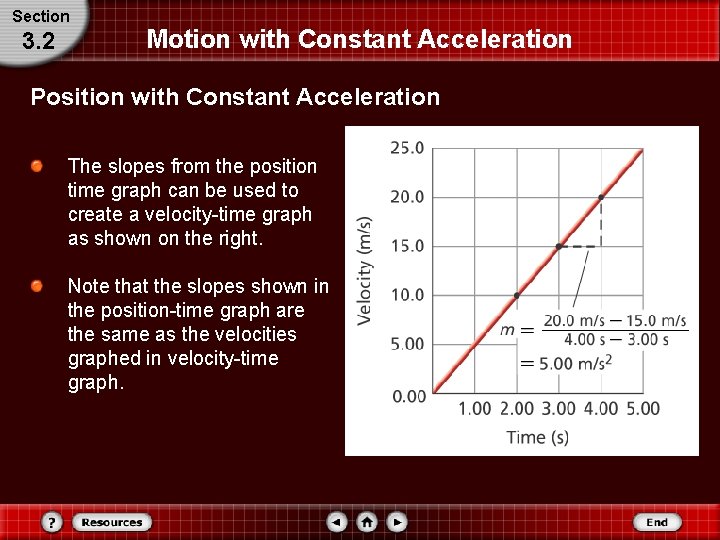
Section 3. 2 Motion with Constant Acceleration Position with Constant Acceleration The slopes from the position time graph can be used to create a velocity-time graph as shown on the right. Note that the slopes shown in the position-time graph are the same as the velocities graphed in velocity-time graph.

Section 3. 2 Motion with Constant Acceleration Position with Constant Acceleration A velocity-time graph does not contain any information about the object’s position. However, the velocity-time graph does contain information about the object’s displacement. Recall that for an object moving at a constant velocity,

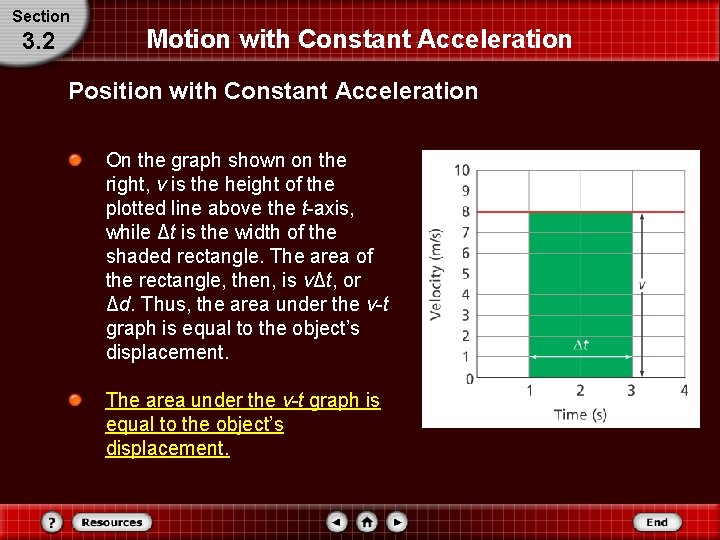
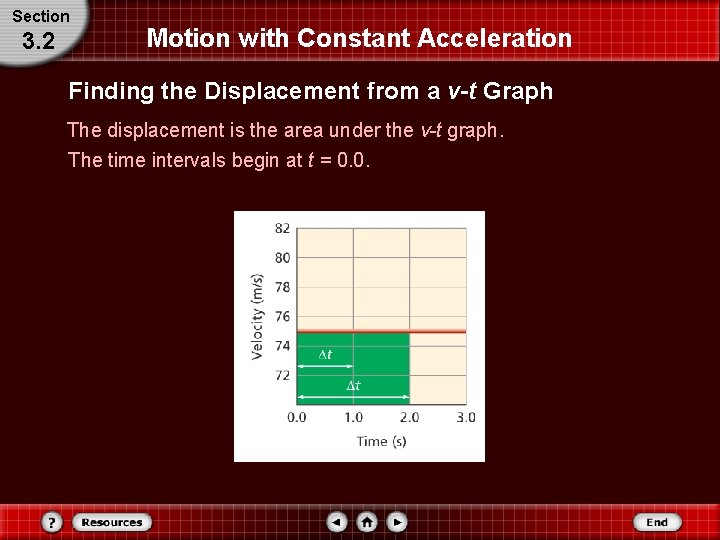
Section 3. 2 Motion with Constant Acceleration Position with Constant Acceleration On the graph shown on the right, v is the height of the plotted line above the t-axis, while Δt is the width of the shaded rectangle. The area of the rectangle, then, is vΔt, or Δd. Thus, the area under the v-t graph is equal to the object’s displacement. The area under the v-t graph is equal to the object’s displacement.

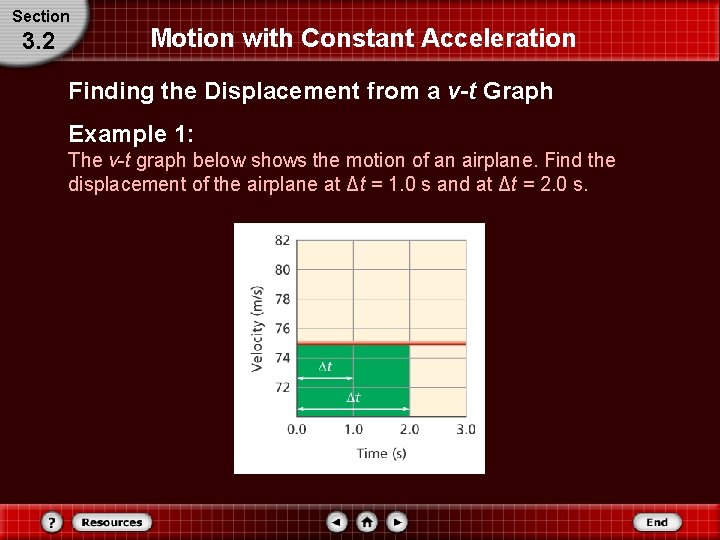
Section 3. 2 Motion with Constant Acceleration Finding the Displacement from a v-t Graph Example 1: The v-t graph below shows the motion of an airplane. Find the displacement of the airplane at Δt = 1. 0 s and at Δt = 2. 0 s.

Section 3. 2 Motion with Constant Acceleration Finding the Displacement from a v-t Graph The displacement is the area under the v-t graph. The time intervals begin at t = 0. 0.

Section 3. 2 Motion with Constant Acceleration Finding the Displacement from a v-t Graph Identify the given and unknown variables. Given: Unknown: v = +75 m/s Δd = ? Δt = 1. 0 s Δt = 2. 0 s

Section Motion with Constant Acceleration 3. 2 Finding the Displacement from a v-t Graph Solve for displacement during Δt = 1. 0 s. Equation: Substitute: v = +75 m/s, Δt = 1. 0 s Solve:

Section 3. 2 Motion with Constant Acceleration Finding the Displacement from a v-t Graph Solve for displacement during Δt = 2. 0 s. Substitute v = +75 m/s, Δt = 2. 0 s

Section Motion with Constant Acceleration 3. 2 Finding the Displacement from a v-t Graph Sense: Are the units correct? Displacement is measured in meters. Do the signs make sense? The positive sign agrees with the graph. Is the magnitude realistic? Moving a distance to about one football field is reasonable for an airplane.

Section 3. 2 Motion with Constant Acceleration An Alternative Expression Often, it is useful to relate position, velocity, and constant acceleration without including time. The three equations for motion with constant acceleration are summarized in the table.

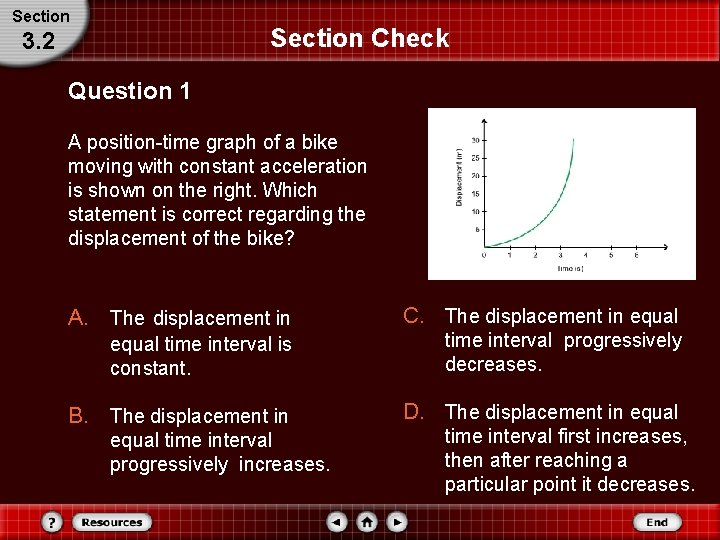
Section Check 3. 2 Question 1 A position-time graph of a bike moving with constant acceleration is shown on the right. Which statement is correct regarding the displacement of the bike? A. The displacement in C. The displacement in equal time interval is constant. time interval progressively decreases. B. The displacement in D. The displacement in equal time interval progressively increases. time interval first increases, then after reaching a particular point it decreases.

Section 3. 2 Section Check Answer 1 Answer: B Reason: You will see that the slope gets steeper as time goes, which means that the displacement in equal time interval progressively gets larger and larger.

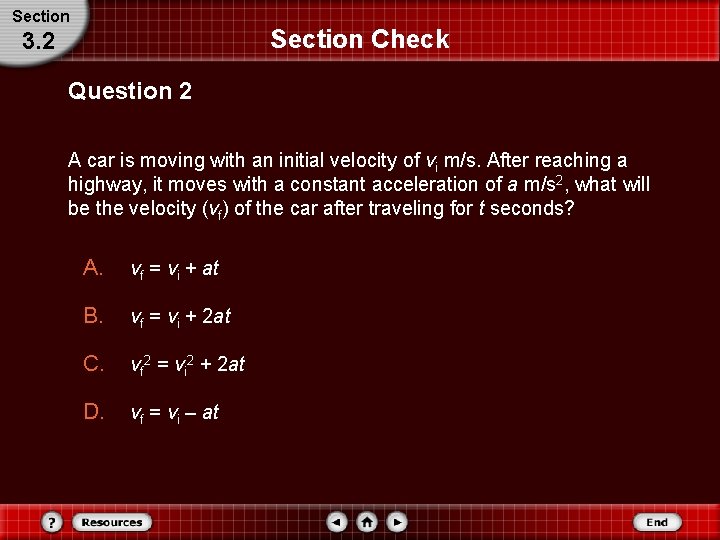
Section Check 3. 2 Question 2 A car is moving with an initial velocity of vi m/s. After reaching a highway, it moves with a constant acceleration of a m/s 2, what will be the velocity (vf) of the car after traveling for t seconds? A. vf = vi + at B. vf = vi + 2 at C. vf 2 = vi 2 + 2 at D. vf = vi – at

Section Check 3. 2 Answer: A Reason: Since a = Δv/Δt vf - vi = a (tf - ti) Also since car is starting from rest, ti = 0 Therefore vf = vi + at (where t is the total time)

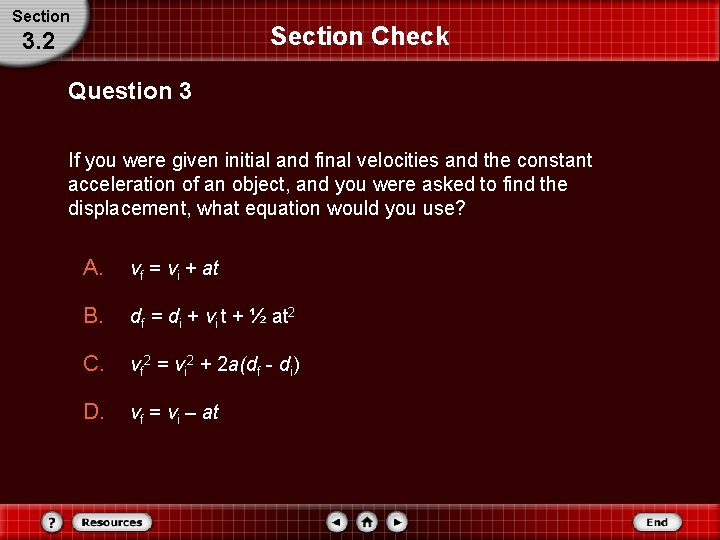
Section Check 3. 2 Question 3 If you were given initial and final velocities and the constant acceleration of an object, and you were asked to find the displacement, what equation would you use? A. vf = vi + at B. df = di + vi t + ½ at 2 C. vf 2 = vi 2 + 2 a(df - di) D. vf = vi – at

Section 3. 2 Section Check Answer 3 Answer: C Reason: Kinematics equation number 3 does not require time. You are not given time in the problem.

Section 3. 2 Please Do Now • Write a question or problem that might occur on the Chapter 3 test. • Pass it to your shoulder partner to answer. • Check their work!

Section 3. 2 Motion with Constant Acceleration Practice Problems p. 65: 20, 21. Section Review p. 71: 34, 39.

Section 3. 2 Please Do Now 1) What does the slope of the line indicate on a position vs. time graph? (Hint: don’t write rise over run) velocity 2) What does the slope of the line indicate on a velocity vs. time graph? acceleration 3) What is the average position between 3 meters and 10 meters? 6. 5 meters 4) How can I find displacement on a velocity vs. time graph? area under the curve

Section Free Fall 3. 3 Free Fall In this section you will: Define acceleration due to gravity. Solve problems involving objects in free fall.

Section 3. 3 Free Fall Acceleration Due to Gravity free fall – the motion of a body when air resistance is negligible and the motion can be considered due to the force of gravity alone. After a lot of observation, Galileo concluded that, neglecting the effect of the air, all objects in free fall had the same acceleration. It didn’t matter what they were made of, how much they weighed, what height they were dropped from, or whether they were dropped or thrown. The acceleration of falling objects, given a special symbol, g, is equal to 9. 80 m/s 2. The acceleration due to gravity is the acceleration of an object in free fall that results from the influence of Earth’s gravity.

Section 3. 3 Free Fall Acceleration Due to Gravity At the top of the flight, the ball’s velocity is 0 m/s. What would happen if its acceleration were also zero? Then, the ball’s velocity would not be changing and would remain at 0 m/s. If this were the case, the ball would not gain any downward velocity and would simply hover in the air at the top of its flight. Because this is not the way objects tossed in the air behave on Earth, you know that the acceleration of an object at the top of its flight must not be zero. Further, because you know that the object will fall from that height, you know that the acceleration must be downward.

Section 3. 3 Free Fall Acceleration Due to Gravity Amusement parks use the concept of free fall to design rides that give the riders the sensation of free fall. These types of rides usually consist of three parts: the ride to the top, momentary suspension, and the plunge downward. When the cars are in free fall, the most massive rider and the least massive rider will have the same acceleration.

Section Free Fall 3. 3 Acceleration Due to Gravity Example: Suppose the free-fall ride at an amusement park starts at rest and is in free fall for 1. 5 s. What would be its velocity at the end of 1. 5 s? How far would it fall? Choose a coordinate system with a positive axis upward and the origin at the initial position of the car. Because the car starts at rest, vi would be equal to 0. 0 m/s. Givens: vi = 0. 0 m/s, di = 0. 0 m, ti = 0. 0 s, tf = 1. 5 s, a = -9. 8 m/s 2 Unknown: vf

Section Free Fall 3. 3 Acceleration Due to Gravity To calculate the final velocity, use the equation for velocity with constant acceleration. Equation: Substitute & Solve: Sense: Negative velocity means down; units are OK.

Section Free Fall 3. 3 Acceleration Due to Gravity How far does the car fall? Use the equation for displacement when time and constant acceleration are known. Equation: Substitute & Solve: Sense: The displacement is negative because it fell, and the units are meters. Looks good!

Section 3. 3 Question 1 What is free fall? Section Check

Section 3. 3 Section Check Answer 1 Free Fall is the motion of the body when air resistance is negligible and the action can be considered due to gravity alone.

Section Check 3. 3 Question 2 If a stone is thrown vertically upwards with a velocity of 25 m/s, what will be the velocity of the stone after 1 second? A. 9. 8 m/s B. 15. 2 m/s C. 25 m/s D. 34. 8 m/s

Section 3. 3 Section Check Answer 2 Answer: B Reason: Since the ball is thrown upwards, the velocity and acceleration are in opposite directions, therefore the speed of the ball decreases. After 1 s, the ball’s velocity is reduced by 9. 8 m/s (as acceleration due to gravity is 9. 8 m/s 2), so it is now traveling at 25 m/s – 9. 8 m/s = 15. 2 m/s.

Section Check 3. 3 Question 3 If a 50 -kg bag and a 100 -kg bag are dropped from a height of 50 m. Which of the following statement is true about their acceleration? (Neglect air resistance) A. 100 -kg bag will fall with a greater acceleration. B. 50 -kg bag will fall with a greater acceleration. C. Both will fall at the same and constant rate of acceleration. D. Both will fall at the same rate of acceleration, which changes equally as time goes.

Section 3. 3 Section Check Answer 3 Answer: C Reason: Any body falling freely towards Earth, falls with a same and constant acceleration of 9. 8 m/s 2. It doesn’t matter how much it weighed and what height it was dropped from.

Section 3. 3 Free Fall Exit Ticket – Please write in full sentences. Describe the velocity and acceleration of a ball that is tossed in the air and comes back down.

Section 3. 3 Free Fall Practice Problems p. 74: 42, 44. HW 3 handout.

Chapter 3 Physics Chapter 2 & 3 Test Information The test is worth 42 points total. Matching : 12 questions, 12 points total Kinematics: 2 questions, 12 points total Graphing: 2 questions, 18 points total Know: - vocabulary for both chapters - how to interpret and draw position-time and velocity-time graphs - how to use the 3 kinematics equations to solve problems - how to express answers with correct units and sig figs