V th ca cc hm s sau trn

VÏ ®å thÞ cña c¸c hµm sè sau trªn cïng mét mÆt ph¼ng to¹

KiÓm tra bµi cò: Các hình sau vẽ đúng hay sai? y y 2

TiÕt 27: HÖ sè gãc cña ® êng th¼ng y = ax + b

y = 2 x 3 TiÕt 27: HÖ sè gãc cña ® êng th¼ng

Slides: 15

Download presentation

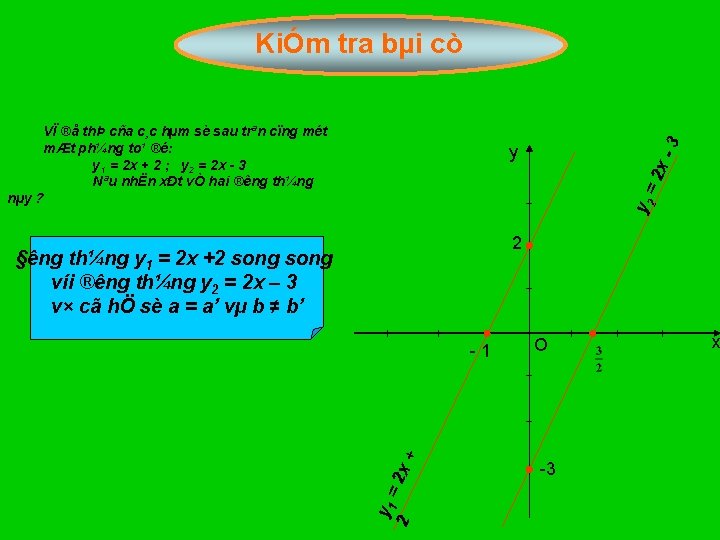
VÏ ®å thÞ cña c¸c hµm sè sau trªn cïng mét mÆt ph¼ng to¹ ®é: y 1 = 2 x + 2 ; y 2 = 2 x 3 Nªu nhËn xÐt vÒ hai ® êng th¼ng nµy ? 3 KiÓm tra bµi cò y 2 =2 x y 2 § êng th¼ng y 1 = 2 x +2 song víi ® êng th¼ng y 2 = 2 x – 3 v× cã hÖ sè a = a’ vµ b ≠ b’ 2 y 1 =2 x+ 1 O 3 x

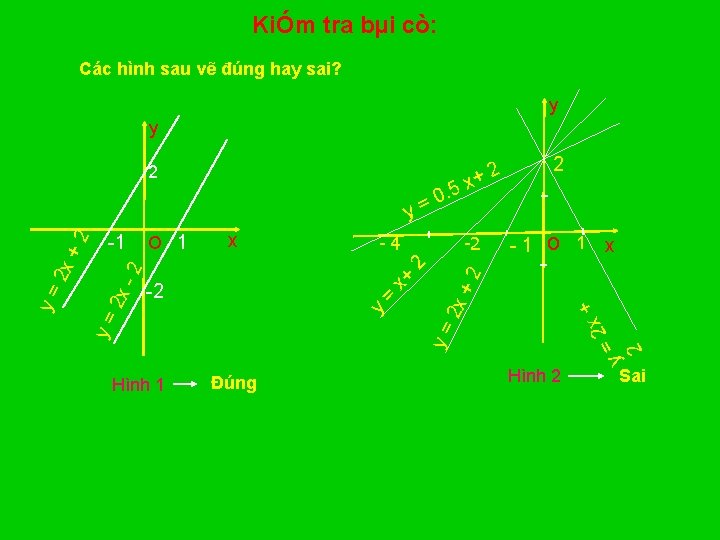
KiÓm tra bµi cò: Các hình sau vẽ đúng hay sai? y y 2 x -4 -2 2 1 O 1 x x =2 y y= 2 + +2 = 2 2 x x+ 2 O 1 y 2 x 2 1 y= y= 2 x +2 y= x 5. 0 +2 Hình 1 Đúng Hình 2 Sai

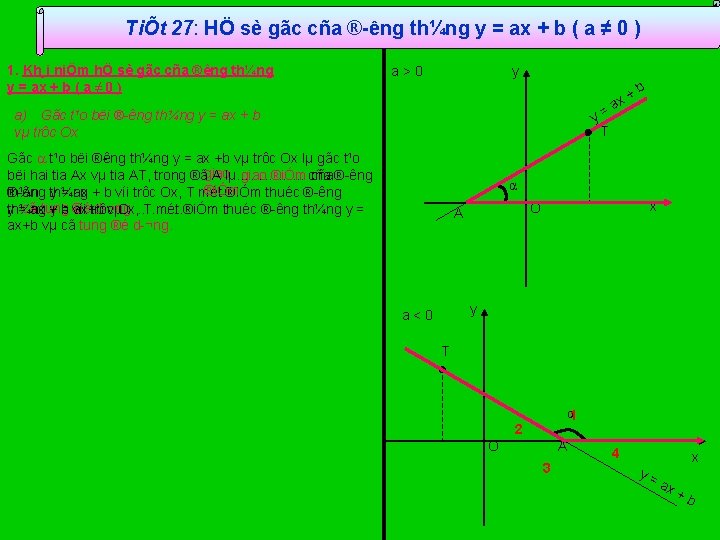
TiÕt 27: HÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) 1. Kh¸i niÖm hÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) a>0 y y= T a) Gãc t¹o bëi ® êng th¼ng y = ax + b vµ trôc Ox Gãc t¹o bëi ® êng th¼ng y = ax +b vµ trôc Ox lµ gãc t¹o bëi hai tia Ax vµ tia AT, trong ®ãgiao A lµ lµ…………. . . giao ®iÓm cña ® êng ®iÓm th¼ng ® êng y = ax + b víi trôc Ox, T mét ®iÓm thuéc ® êng d ¬ng. yth¼ng =cã axtung +y b = ®é víi ax+b trôc vµ…………… Ox, T mét ®iÓm thuéc ® êng th¼ng y = ax+b vµ cã tung ®é d ¬ng. + ax b α x O A y a<0 T α 1 2 A O 3 4 y= x ax +b

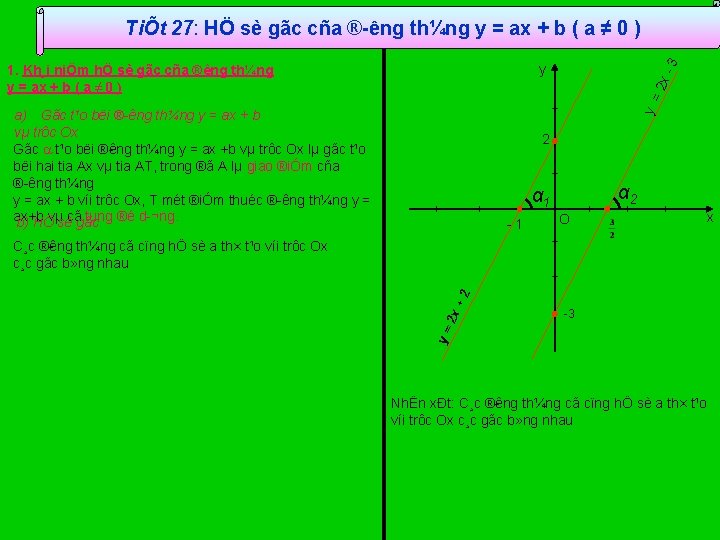
y = 2 x 3 TiÕt 27: HÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) y 1. Kh¸i niÖm hÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) a) Gãc t¹o bëi ® êng th¼ng y = ax + b vµ trôc Ox Gãc t¹o bëi ® êng th¼ng y = ax +b vµ trôc Ox lµ gãc t¹o bëi hai tia Ax vµ tia AT, trong ®ã A lµ giao ®iÓm cña ® êng th¼ng y = ax + b víi trôc Ox, T mét ®iÓm thuéc ® êng th¼ng y = ax+b tung ®é d ¬ng. b) HÖvµsècãgãc 2 α 1 1 O 3 y= 2 x +2 Çc ® êng th¼ng cã cïng hÖ sè a th× t¹o víi trôc Ox çc gãc b» ng nhau NhËn xÐt: Çc ® êng th¼ng cã cïng hÖ sè a th× t¹o víi trôc Ox çc gãc b» ng nhau x

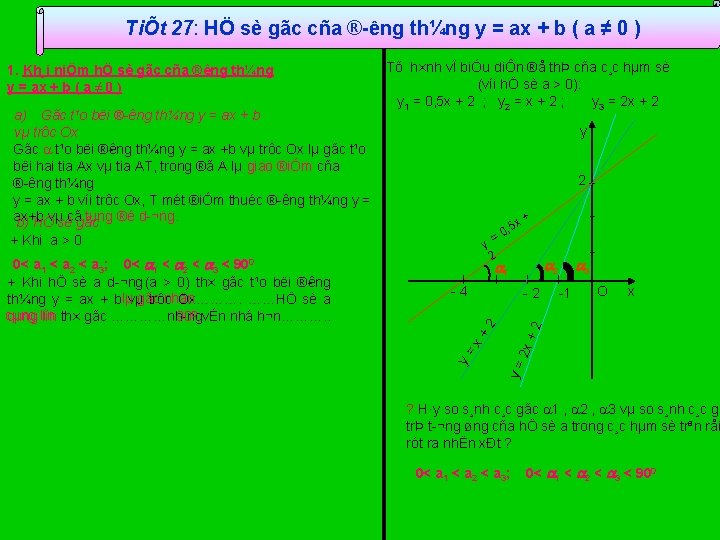
TiÕt 27: HÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) y 2 + Khi a > 0 + 2 2 1 4 3 1 O x +2 2 2 x+ y= 0< a 1 < a 2 < a 3; 0< 1 < 2 < 3 < 900 + Khi hÖ sè a d ¬ng (a > 0) th× gãc t¹o bëi ® êng nhän th¼ng y = ax + b lµvµgãc trôc Ox………. ……HÖ sè a cµng 900. vÉn nhá h¬n………. . cµng lín th× gãc …………nh ng y , 5 x 0 = 2 x a) Gãc t¹o bëi ® êng th¼ng y = ax + b vµ trôc Ox Gãc t¹o bëi ® êng th¼ng y = ax +b vµ trôc Ox lµ gãc t¹o bëi hai tia Ax vµ tia AT, trong ®ã A lµ giao ®iÓm cña ® êng th¼ng y = ax + b víi trôc Ox, T mét ®iÓm thuéc ® êng th¼ng y = ax+b tung ®é d ¬ng. b) HÖvµsècãgãc Tõ h×nh vÏ biÓu diÔn ®å thÞ cña çc hµm sè (víi hÖ sè a > 0): y 1 = 0, 5 x + 2 ; y 2 = x + 2 ; y 3 = 2 x + 2 y= 1. Kh¸i niÖm hÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) ? H·y so s¸nh çc gãc 1 , 2 , 3 vµ so s¸nh çc gi trÞ t ¬ng øng cña hÖ sè a trong çc hµm sè trªn råi rót ra nhËn xÐt ? 0< a 1 < a 2 < a 3; 0< 1 < 2 < 3 < 900

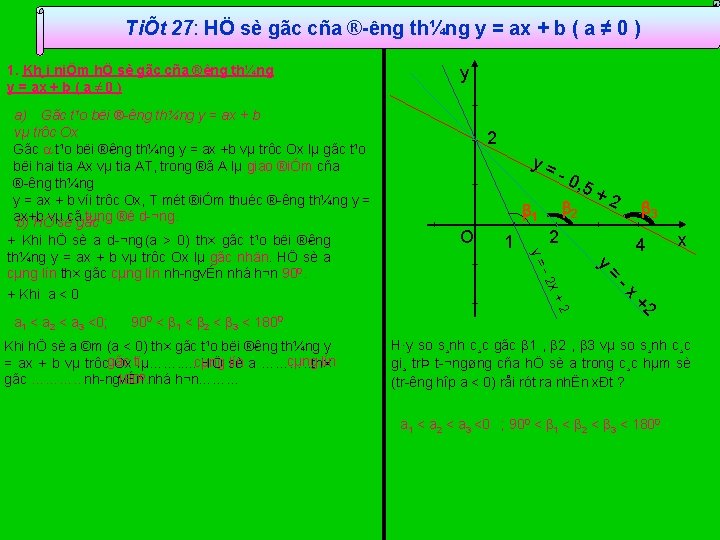
TiÕt 27: HÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) 1. Kh¸i niÖm hÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) a) Gãc t¹o bëi ® êng th¼ng y = ax + b vµ trôc Ox Gãc t¹o bëi ® êng th¼ng y = ax +b vµ trôc Ox lµ gãc t¹o bëi hai tia Ax vµ tia AT, trong ®ã A lµ giao ®iÓm cña ® êng th¼ng y = ax + b víi trôc Ox, T mét ®iÓm thuéc ® êng th¼ng y = ax+b tung ®é d ¬ng. b) HÖvµsècãgãc , 5 + 2 1 O 1 2 2 3 4 x y = x +2 2 Khi hÖ sè a ©m (a < 0) th× gãc t¹o bëi ® êng th¼ng y cµng lín a ………. . th× = ax + b vµ trôcgãc Ox tïlµ……. . . cµng HÖ sè 0 gãc ………. . nh ng 180 vÉn. nhá h¬n……… 0 x+ 900 < 1 < 2 < 3 < 1800 y= 2 a 1 < a 2 < a 3 <0; 2 y= + Khi hÖ sè a d ¬ng (a > 0) th× gãc t¹o bëi ® êng th¼ng y = ax + b vµ trôc Ox lµ gãc nhän. HÖ sè a cµng lín th× gãc cµng lín nh ngvÉn nhá h¬n 900. + Khi a < 0 y H·y so s¸nh çc gãc 1 , 2 , 3 vµ so s¸nh çc gi¸ trÞ t ¬ng øng cña hÖ sè a trong çc hµm sè (tr êng hîp a < 0) råi rót ra nhËn xÐt ? a 1 < a 2 < a 3 <0 ; 900 < 1 < 2 < 3 < 1800

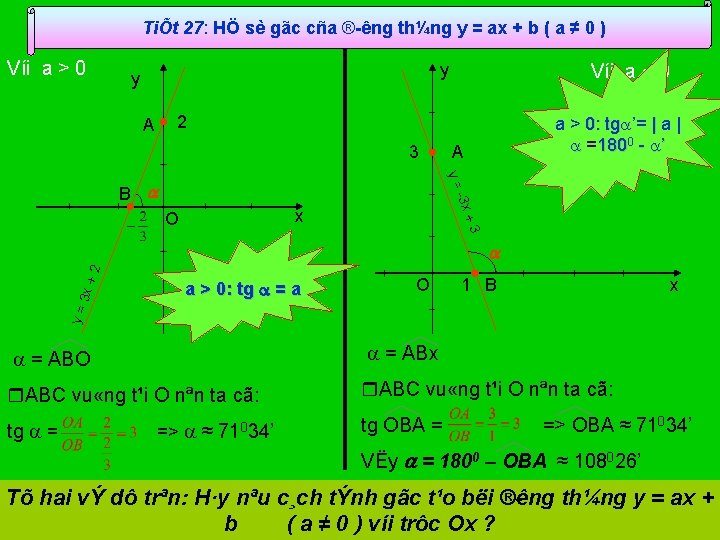
TiÕt 27: HÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) Víi a > 0 y y Víi a < 0 a > 0: tg ’= | a | =1800 ’ 2 A 3 A y= 3 x B +3 x O a > 0: tg = a O x 1 B y= 3 x + 2 = ABO = ABx ABC vu «ng t¹i O nªn ta cã: tg = tg OBA = => ≈ 71034’ => OBA ≈ 71034’ VËy = 1800 – OBA ≈ 108026’ Tõ hai vÝ dô trªn: H·y nªu c¸ch tÝnh gãc t¹o bëi ® êng th¼ng y = ax + b ( a ≠ 0 ) víi trôc Ox ?

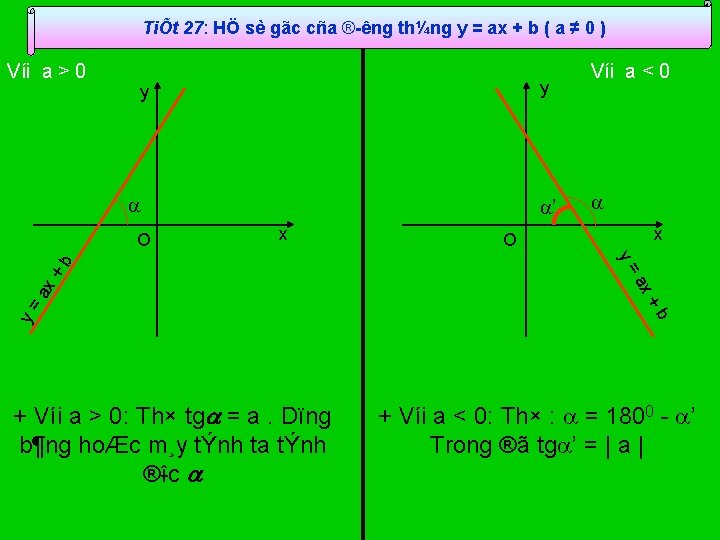
TiÕt 27: HÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) Víi a > 0 y y x ax + +b y= x O ax + Víi a > 0: Th× tg = a. Dïng b¶ng hoÆc m¸y tÝnh ta tÝnh ® îc y= b O ’ Víi a < 0 + Víi a < 0: Th× : = 1800 ’ Trong ®ã tg ’ = | a |

TiÕt 27: HÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) 1. Kh¸i niÖm hÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) a) Gãc t¹o bëi ® êng th¼ng y = ax + b vµ trôc Ox Gãc t¹o bëi ® êng th¼ng y = ax +b vµ trôc Ox lµ gãc t¹o bëi hai tia Ax vµ tia AT, trong ®ã A lµ giao ®iÓm cña ® êng th¼ng y = ax + b víi trôc Ox, T mét ®iÓm thuéc ® êng th¼ng y = ax+b tung ®é d ¬ng. b) HÖvµsècãgãc a lµ hÖ sè gãc cña ® êng th¼ng y = ax + b 2. VÝ dô C¸ch tÝnh gãc t¹o bëi ® êng th¼ng y = ax + b víi trôc Ox + Víi a > 0: Th× tg = a + Víi a < 0: Th× : = 1800 ’ Trong ®ã tg ’ = | a | Bài tập 2: Không cần vẽ, hãy tính góc tạo bởi đường thẳng sau và trục Ox: a) y = 2 x – 1; b) y = 2 x + 1 Bài tập 3: Tìm hệ số góc của đường thẳng y = ax + b, biết đường thẳng tạo với trục Ox một góc 600

TiÕt 27: HÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) 1. Kh¸i niÖm hÖ sè gãc cña ® êng th¼ng y = ax + b ( a ≠ 0 ) a) Gãc t¹o bëi ® êng th¼ng y = ax + b vµ trôc Ox Gãc t¹o bëi ® êng th¼ng y = ax +b vµ trôc Ox lµ gãc t¹o bëi hai tia Ax vµ tia AT, trong ®ã A lµ giao ®iÓm cña ® êng th¼ng y = ax + b víi trôc Ox, T mét ®iÓm thuéc ® êng th¼ng y = ax+b vµ sè cã gãc tung ®é d ¬ng. b) HÖ a lµ hÖ sè gãc cña ® êng th¼ng y = ax + b 2. VÝ dô Çch tÝnh gãc t¹o bëi ® êng th¼ng y = ax + b víi trôc Ox + Víi a > 0: Th× tg = a + Víi a < 0: Th× : = 1800 ’ Trong ®ã tg ’ = | a | 3. Cñng cè H íng dÉn vÒ nhµ: HiÓu vµ n¾m v÷ng nh÷ng kiÕn thøc cña bµi häc. *Kh¸i niÖm gãc t¹o bëi ® êngth¼ng y= ax +b ( a ≠ 0) vµ trôc Ox, hÖ sè gãc cña ® êng th¼ng. *Mèi liªn hÖ mËt thiÕt gi÷a hÖ sè gãc a vµ gãc t¹o bëi ® êng th¼ng y = ax +b (a ≠ 0) vµ trôc Ox. *Çch tÝnh gãc t¹o bëi ® êngth¼ng y= ax +b ( a ≠ 0) vµ trôc Ox trong hai tr ênghîp a >0 vµ tr ênghîp a <0. Lµm çc bµi tËp 27, 28, , 29 (SGK trang 58, 59) HD bµi 30: ¸p dông c «ng thøc Khi ®iÓm A(x 1; y 1) vµ B (x 2; y 2)