UNIVERSIDAD NACIONAL EXPERIMENTAL POLITCNICA ANTONIO JOS DE SUCRE

UNIVERSIDAD NACIONAL EXPERIMENTAL POLITÉCNICA “ANTONIO JOSÉ DE SUCRE” VICE-RECTORADO PUERTO ORDAZ DEPARTAMENTO DE ESTUDIOS GENERALES SECCIÓN DE MATEMÁTICAS CÁTEDRA DE DIBUJO I EL PLANO EN EL SISTEMA DIEDRICO. PUNTO. Y RECTA DEL PLANO. TRAZAS. Thamara Girón

CONTENIDO n EL PLANO EN EL SISTEMA DIEDRICO n POSICIÓN DE UN PUNTO EN EL PLANO n n POSICIÓN DE LAS RECTAS PARTICULARES DEL PLANO TRAZAS DEL PLANO

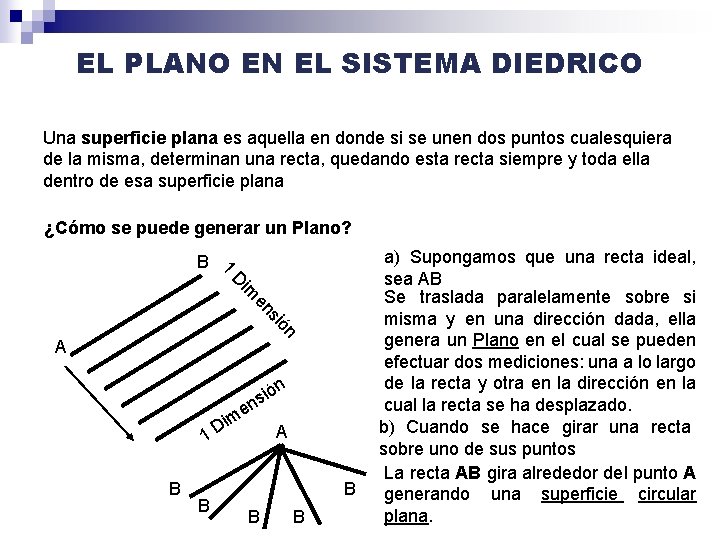
EL PLANO EN EL SISTEMA DIEDRICO Una superficie plana es aquella en donde si se unen dos puntos cualesquiera de la misma, determinan una recta, quedando esta recta siempre y toda ella dentro de esa superficie plana ¿Cómo se puede generar un Plano? 1 B D si en im ón A ión s en m i D 1 B B A B B B a) Supongamos que una recta ideal, sea AB Se traslada paralelamente sobre si misma y en una dirección dada, ella genera un Plano en el cual se pueden efectuar dos mediciones: una a lo largo de la recta y otra en la dirección en la cual la recta se ha desplazado. b) Cuando se hace girar una recta sobre uno de sus puntos La recta AB gira alrededor del punto A generando una superficie circular plana.

Representación del plano n La posición de un plano en el espacio queda determinado: av ¨ ¨ n Tres puntos no alineados Dos rectas que se cortan Dos rectas paralelas Una recta y un punto exterior de ella Hay que tener presente que: Av rv bv Ah rh bh En un plano hay infinidades de rectas ah Su figura descriptiva, se basará en las proyecciones de los elementos que componen el plano. ¨ Una recta pertenece a un plano, si pasa por dos puntos pertenecientes a este plano. ¨ ¨

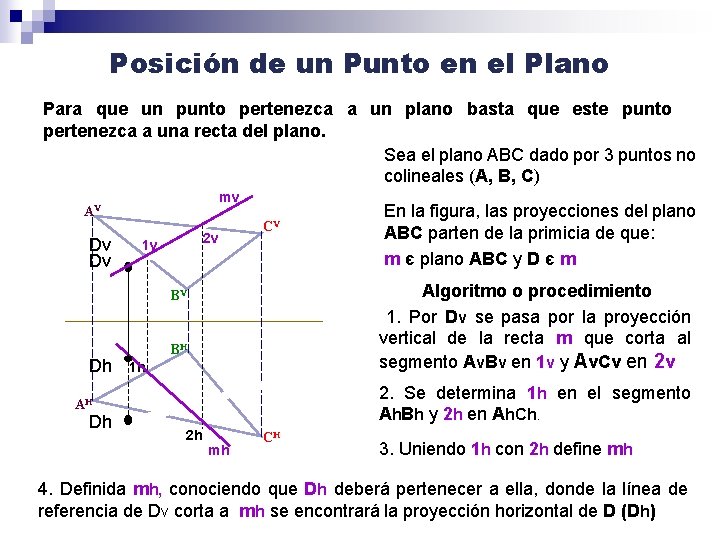
Posición de un Punto en el Plano Para que un punto pertenezca a un plano basta que este punto pertenezca a una recta del plano. Sea el plano ABC dado por 3 puntos no colineales (A, B, C) mv m. V AV Dv Dv 2 v 1 v CV Algoritmo o procedimiento 1. Por Dv se pasa por la proyección vertical de la recta m que corta al segmento Av. Bv en 1 v y Av. Cv en 2 v BV Dh BH 1 h m. H 2. Se determina 1 h en el segmento Ah. Bh y 2 h en Ah. Ch. AH Dh 2 h En la figura, las proyecciones del plano ABC parten de la primicia de que: m є plano ABC y D є m mh CH 3. Uniendo 1 h con 2 h define mh 4. Definida mh, conociendo que Dh deberá pertenecer a ella, donde la línea de referencia de Dv corta a mh se encontrará la proyección horizontal de D (Dh)

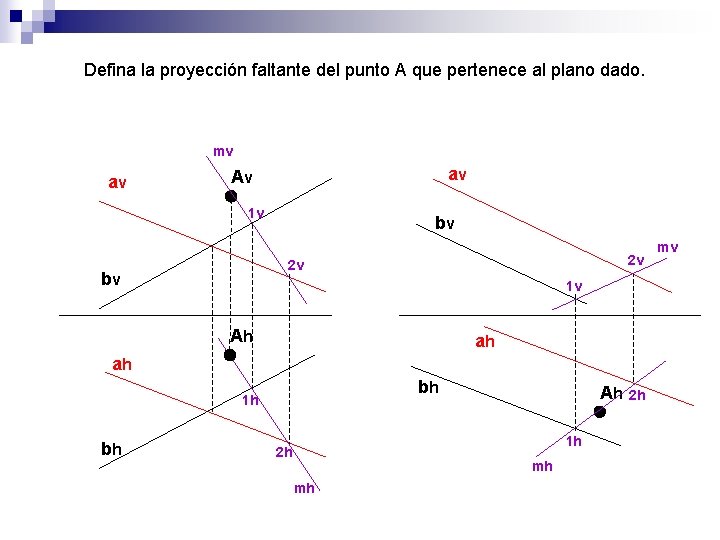
Defina la proyección faltante del punto A que pertenece al plano dado. mv av av Av 1 v bv 2 v 2 v bv 1 v Ah ah ah bh 1 h bh Ah 1 h 2 h mh mh 2 h mv

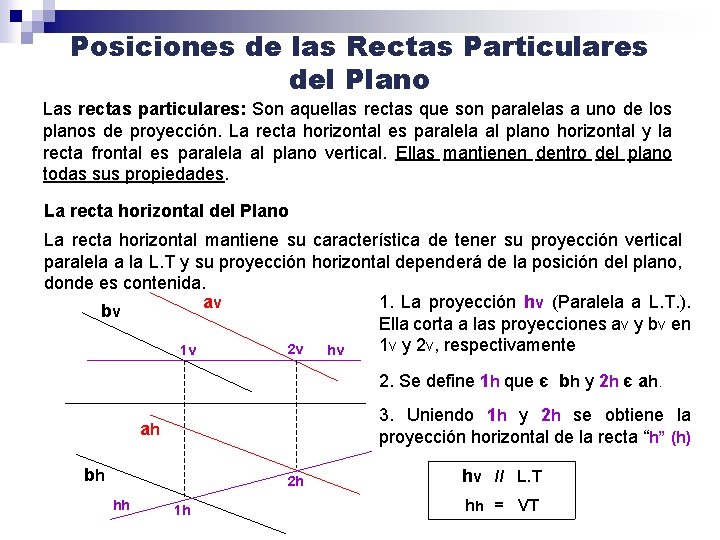
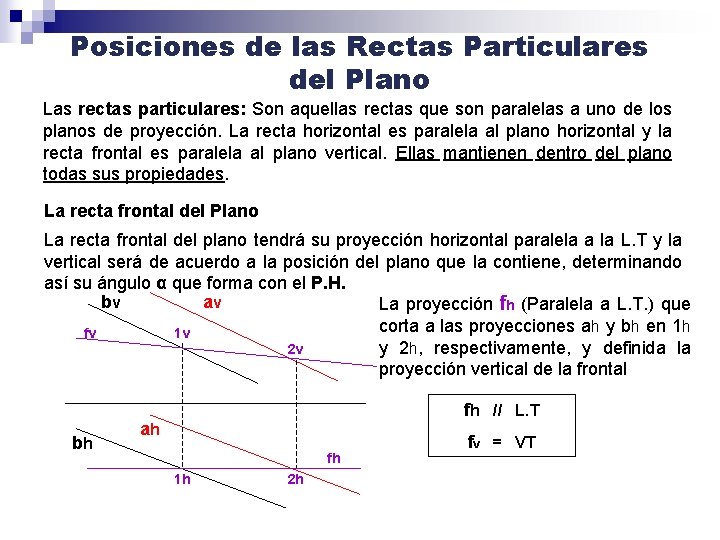
Posiciones de las Rectas Particulares del Plano Las rectas particulares: Son aquellas rectas que son paralelas a uno de los planos de proyección. La recta horizontal es paralela al plano horizontal y la recta frontal es paralela al plano vertical. Ellas mantienen dentro del plano todas sus propiedades. La recta horizontal del Plano La recta horizontal mantiene su característica de tener su proyección vertical paralela a la L. T y su proyección horizontal dependerá de la posición del plano, donde es contenida. av 1. La proyección hv (Paralela a L. T. ). bv Ella corta a las proyecciones av y bv en 1 v y 2 v, respectivamente 2 v 1 v hv 2. Se define 1 h que є bh y 2 h є ah. 3. Uniendo 1 h y 2 h se obtiene la proyección horizontal de la recta “h” (h) ah bh 2 h hh 1 h hv // L. T hh = VT

Posiciones de las Rectas Particulares del Plano Las rectas particulares: Son aquellas rectas que son paralelas a uno de los planos de proyección. La recta horizontal es paralela al plano horizontal y la recta frontal es paralela al plano vertical. Ellas mantienen dentro del plano todas sus propiedades. La recta frontal del Plano La recta frontal del plano tendrá su proyección horizontal paralela a la L. T y la vertical será de acuerdo a la posición del plano que la contiene, determinando así su ángulo α que forma con el P. H. bv av La proyección fh (Paralela a L. T. ) que corta a las proyecciones ah y bh en 1 h fv 1 v y 2 h, respectivamente, y definida la 2 v proyección vertical de la frontal bh fh // L. T ah fh 1 h 2 h fv = VT

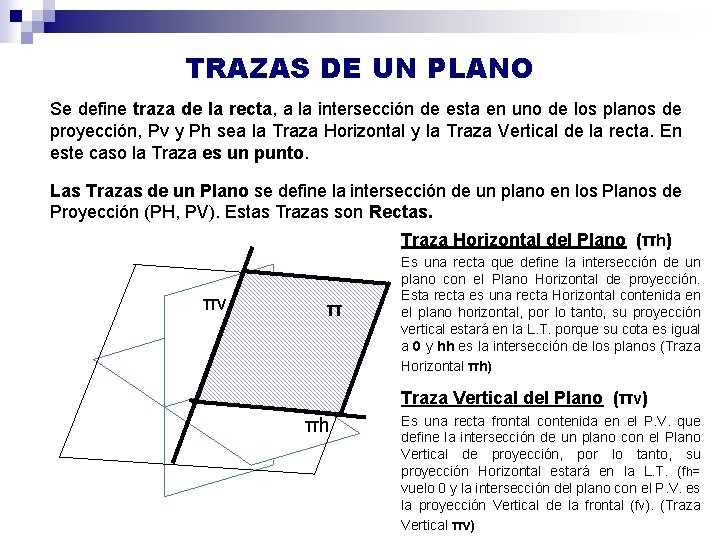
TRAZAS DE UN PLANO Se define traza de la recta, a la intersección de esta en uno de los planos de proyección, Pv y Ph sea la Traza Horizontal y la Traza Vertical de la recta. En este caso la Traza es un punto. Las Trazas de un Plano se define la intersección de un plano en los Planos de Proyección (PH, PV). Estas Trazas son Rectas. Traza Horizontal del Plano (πh) πv π Es una recta que define la intersección de un plano con el Plano Horizontal de proyección. Esta recta es una recta Horizontal contenida en el plano horizontal, por lo tanto, su proyección vertical estará en la L. T. porque su cota es igual a 0 y hh es la intersección de los planos (Traza Horizontal πh) Traza Vertical del Plano (πv) πh Es una recta frontal contenida en el P. V. que define la intersección de un plano con el Plano Vertical de proyección, por lo tanto, su proyección Horizontal estará en la L. T. (fh= vuelo 0 y la intersección del plano con el P. V. es la proyección Vertical de la frontal (fv). (Traza Vertical πv)

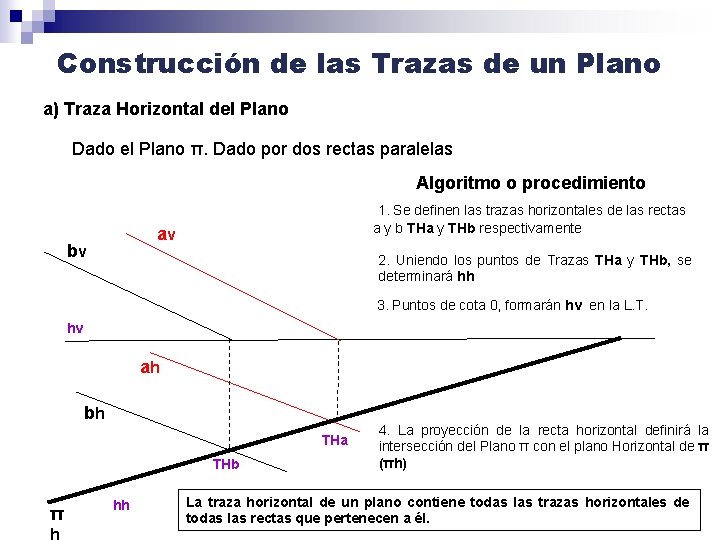
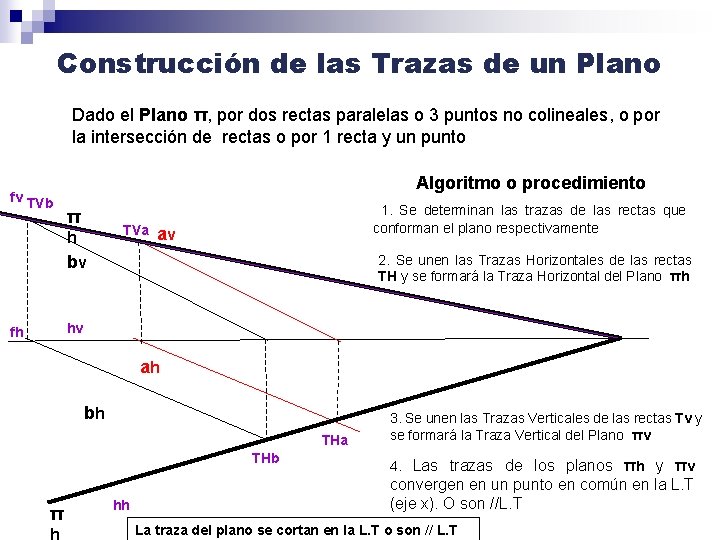
Construcción de las Trazas de un Plano a) Traza Horizontal del Plano Dado el Plano π. Dado por dos rectas paralelas Algoritmo o procedimiento 1. Se definen las trazas horizontales de las rectas a y b THa y THb respectivamente av bv 2. Uniendo los puntos de Trazas THa y THb, se determinará hh 3. Puntos de cota 0, formarán hv en la L. T. hv ah bh THa THb π h hh 4. La proyección de la recta horizontal definirá la intersección del Plano π con el plano Horizontal de π (πh) La traza horizontal de un plano contiene todas las trazas horizontales de todas las rectas que pertenecen a él.

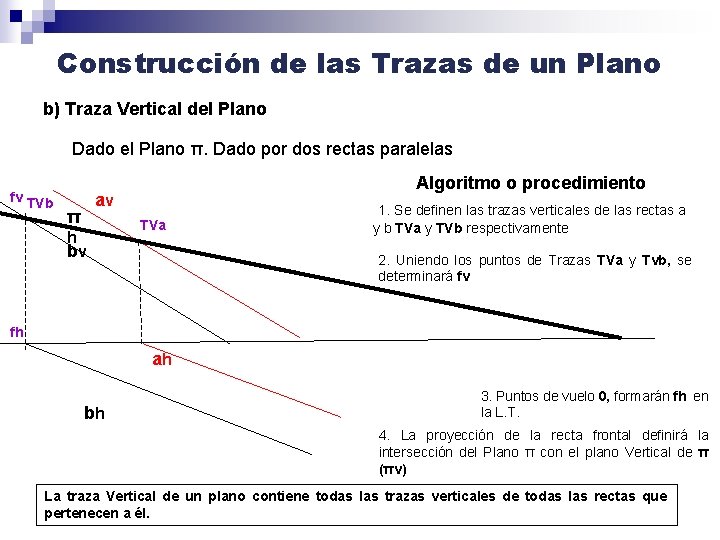
Construcción de las Trazas de un Plano b) Traza Vertical del Plano Dado el Plano π. Dado por dos rectas paralelas fv TVb Algoritmo o procedimiento av π TVa h bv 1. Se definen las trazas verticales de las rectas a y b TVa y TVb respectivamente 2. Uniendo los puntos de Trazas TVa y Tvb, se determinará fv fh ah bh 3. Puntos de vuelo 0, formarán fh en la L. T. 4. La proyección de la recta frontal definirá la intersección del Plano π con el plano Vertical de π (πv) La traza Vertical de un plano contiene todas las trazas verticales de todas las rectas que pertenecen a él.

Construcción de las Trazas de un Plano Dado el Plano π, por dos rectas paralelas o 3 puntos no colineales, o por la intersección de rectas o por 1 recta y un punto fv TVb Algoritmo o procedimiento π TVa h 1. Se determinan las trazas de las rectas que conforman el plano respectivamente av bv 2. Se unen las Trazas Horizontales de las rectas TH y se formará la Traza Horizontal del Plano πh hv fh ah bh THa THb π h hh 3. Se unen las Trazas Verticales de las rectas Tv y se formará la Traza Vertical del Plano πv 4. Las trazas de los planos πh y πv convergen en un punto en común en la L. T (eje x). O son //L. T La traza del plano se cortan en la L. T o son // L. T

EJERCICIOS n 1. Determinar las trazas de las rectas a A (40, 30, 70) B (70, 60, 20) b C (80, 10, 60) 2. π A (30, 40) B (80, -40, 25) C (95, -25, 60) 3. π A (5, 35, 10) B (15, 27, 35) C (45, 40, 60) M (100, __, 25)

POSICIONES PARTICULARES DE LOS PLANOS CON RESPECTO A LOS PLANOS DE PROYECCIÓN n Los planos pueden tener diferentes posiciones con respecto a los planos de proyección (PH, PV, PL) n Las posiciones del plano se pueden agrupar en 3 relaciones, cuando: ü El plano no es perpendicular a los planos PH, PV. ü El plano es perpendicular a uno de los planos de proyección ü El plano es perpendicular a dos de los planos de proyección.

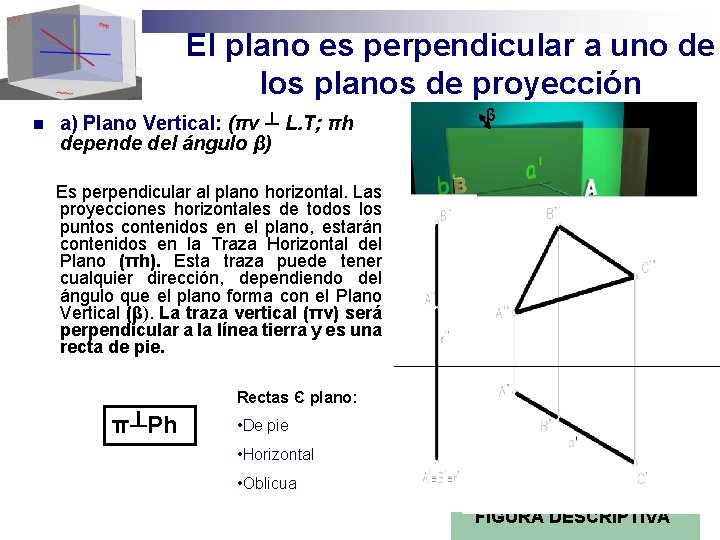
El plano es perpendicular a uno de los planos de proyección n a) Plano Vertical: (πv ┴ L. T; πh depende del ángulo β) Es perpendicular al plano horizontal. Las proyecciones horizontales de todos los puntos contenidos en el plano, estarán contenidos en la Traza Horizontal del Plano (πh). Esta traza puede tener cualquier dirección, dependiendo del ángulo que el plano forma con el Plano Vertical (β). La traza vertical (πv) será perpendicular a la línea tierra y es una recta de pie. β FIGURA ESPACIAL Rectas Є plano: π┴Ph • De pie • Horizontal • Oblicua FIGURA ESPACIAL FIGURA DESCRIPTIVA

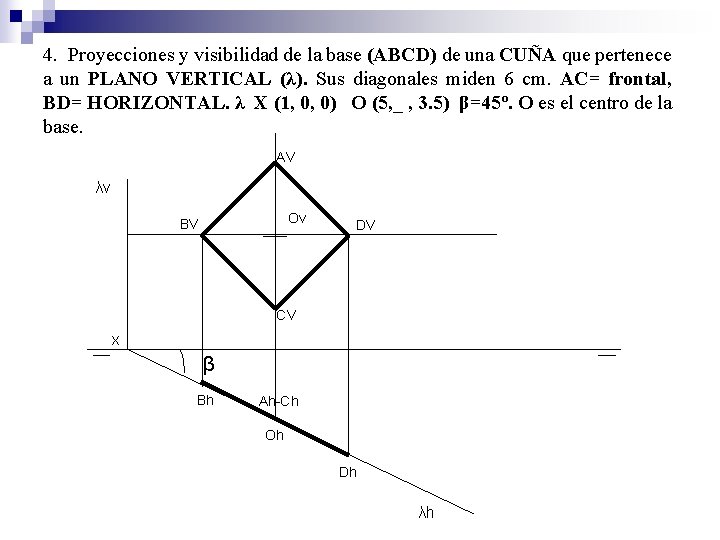
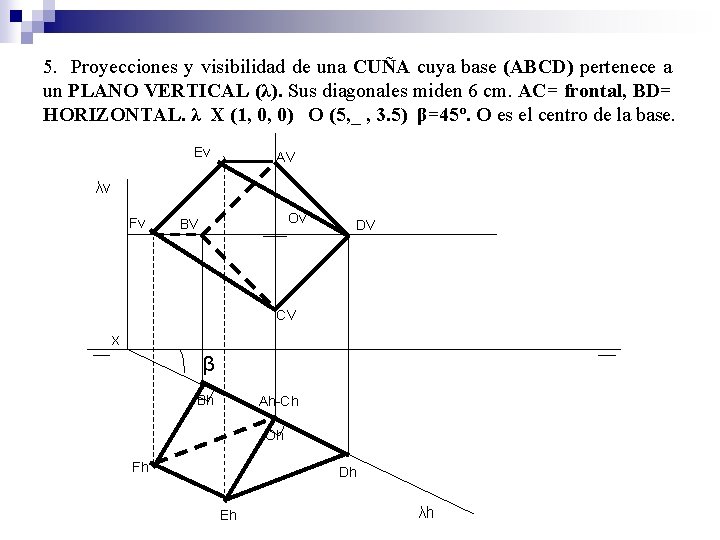
4. Proyecciones y visibilidad de la base (ABCD) de una CUÑA que pertenece a un PLANO VERTICAL (λ). Sus diagonales miden 6 cm. AC= frontal, BD= HORIZONTAL. λ X (1, 0, 0) O (5, _ , 3. 5) β=45º. O es el centro de la base. AV λv Ov BV DV CV X β Bh Ah-Ch Oh Dh λh

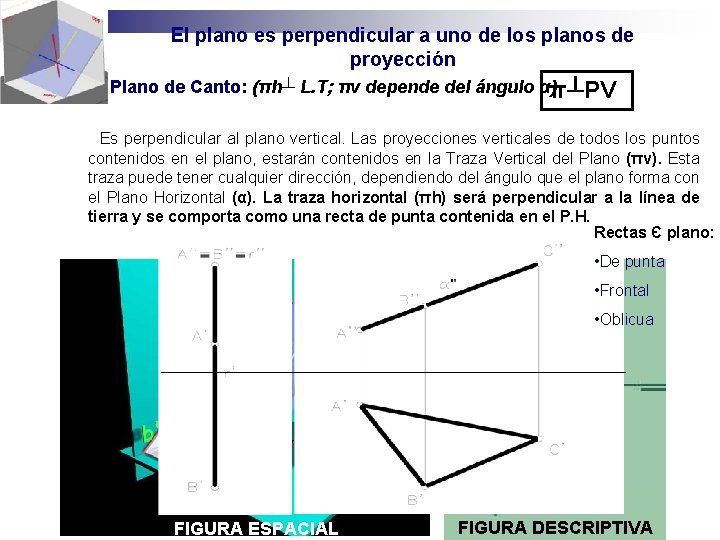
El plano es perpendicular a uno de los planos de proyección n b) Plano de Canto: (πh┴ L. T; πv depende del ángulo α)π┴PV Es perpendicular al plano vertical. Las proyecciones verticales de todos los puntos contenidos en el plano, estarán contenidos en la Traza Vertical del Plano (πv). Esta traza puede tener cualquier dirección, dependiendo del ángulo que el plano forma con el Plano Horizontal (α). La traza horizontal (πh) será perpendicular a la línea de tierra y se comporta como una recta de punta contenida en el P. H. Rectas Є plano: • De punta • Frontal • Oblicua FIGURA ESPACIAL α FIGURA ESPACIAL FIGURA DESCRIPTIVA

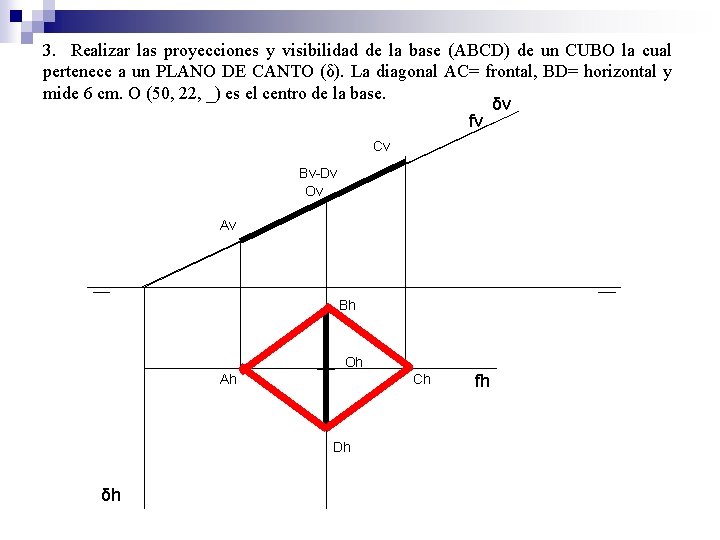
3. Realizar las proyecciones y visibilidad de la base (ABCD) de un CUBO la cual pertenece a un PLANO DE CANTO (δ). La diagonal AC= frontal, BD= horizontal y mide 6 cm. O (50, 22, _) es el centro de la base. δv fv Cv Bv-Dv Ov Av Bh Oh Ah Ch Dh δh fh

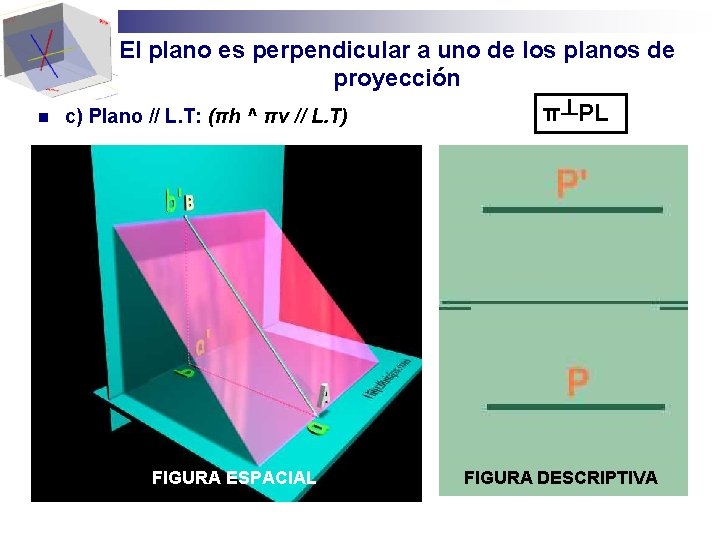
n El plano es perpendicular a uno de los planos de proyección π┴PL c) Plano // L. T: (πh ^ πv // L. T) FIGURA ESPACIAL FIGURA DESCRIPTIVA

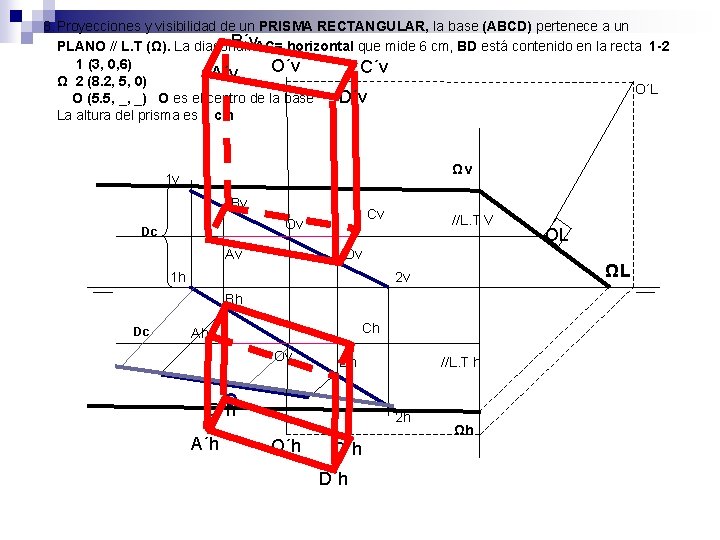
7. Proyecciones y visibilidad de la base (ABCD) de un PRISMA RECTANGULAR, que pertenece a un PLANO // L. T (Ω). La diagonal. AC= horizontal que mide 6 cm, BD está contenido en la recta 1 -2 1 (3, 0, 6) Ω 2 (8. 2, 5, 0) O (5. 5, _, _) O es el centro de la base Ωv 1 v Bv Cv Ov Dc Av //L. T V Dv 2 v 1 h Bh Dc Ch Ah Ov O Dh //L. T h 2 h Ωh

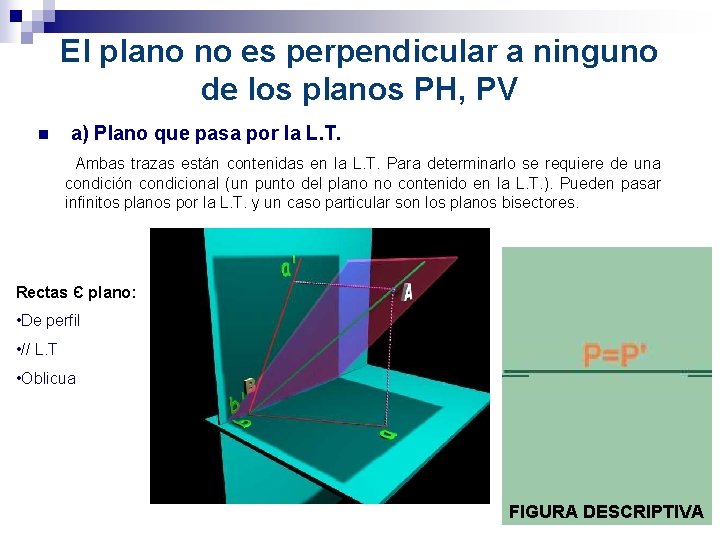
El plano no es perpendicular a ninguno de los planos PH, PV n a) Plano que pasa por la L. T. Ambas trazas están contenidas en la L. T. Para determinarlo se requiere de una condición condicional (un punto del plano no contenido en la L. T. ). Pueden pasar infinitos planos por la L. T. y un caso particular son los planos bisectores. Rectas Є plano: • De perfil • // L. T • Oblicua FIGURA ESPACIAL FIGURA DESCRIPTIVA

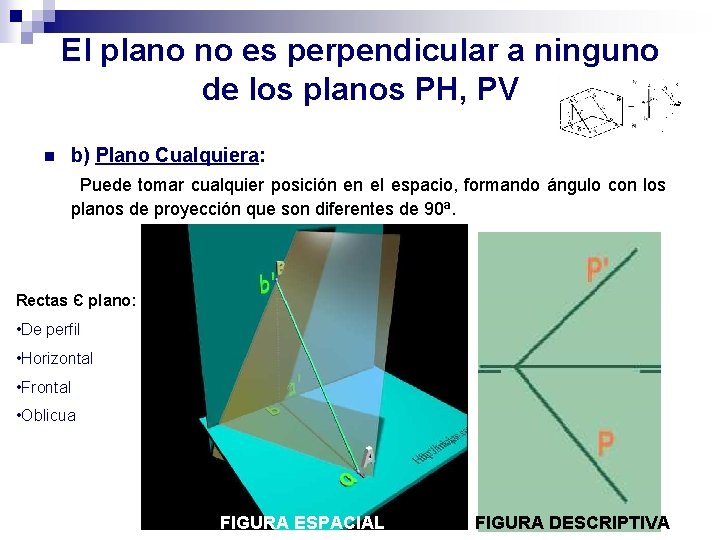
El plano no es perpendicular a ninguno de los planos PH, PV n b) Plano Cualquiera: Puede tomar cualquier posición en el espacio, formando ángulo con los planos de proyección que son diferentes de 90ª. Rectas Є plano: • De perfil • Horizontal • Frontal • Oblicua FIGURA ESPACIAL FIGURA DESCRIPTIVA

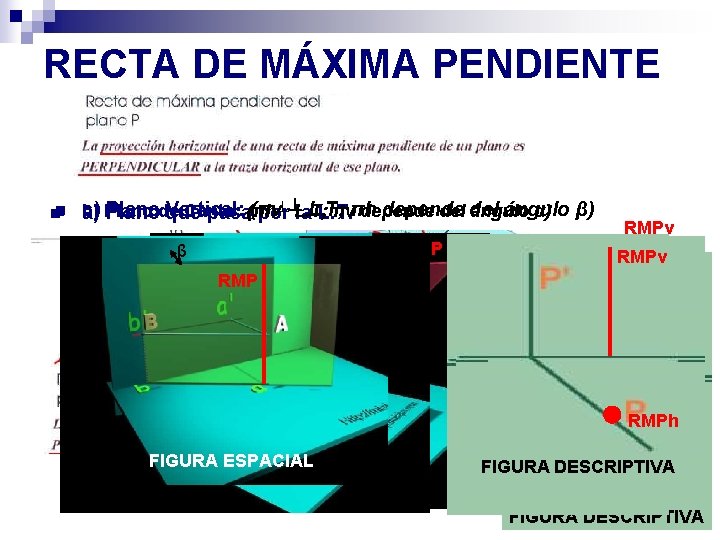
RECTA DE MÁXIMA PENDIENTE c) Planode Vertical: (πv depende ángulo n a) b) Plano Canto: πvπh depende del ángulo α) nn que pasa(πh┴ por┴L. T; la. L. T; L. T. RMP β RMP FIGURA ESPACIAL RMP β) RMPv RMPh FIGURA DESCRIPTIVA

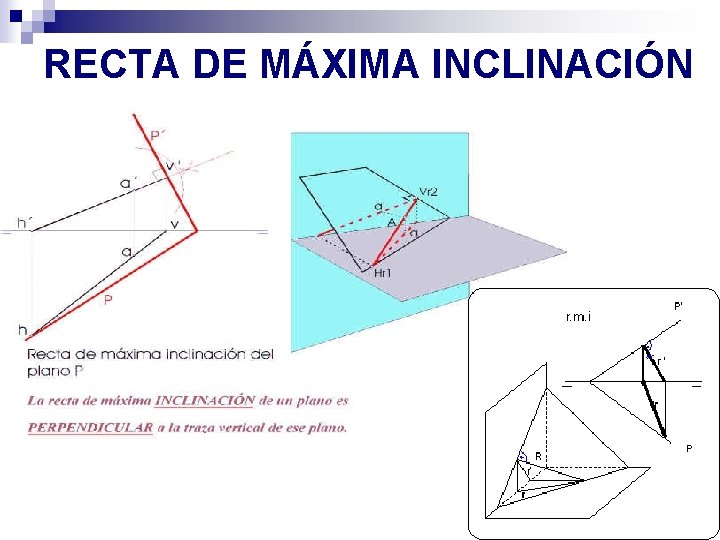
RECTA DE MÁXIMA INCLINACIÓN

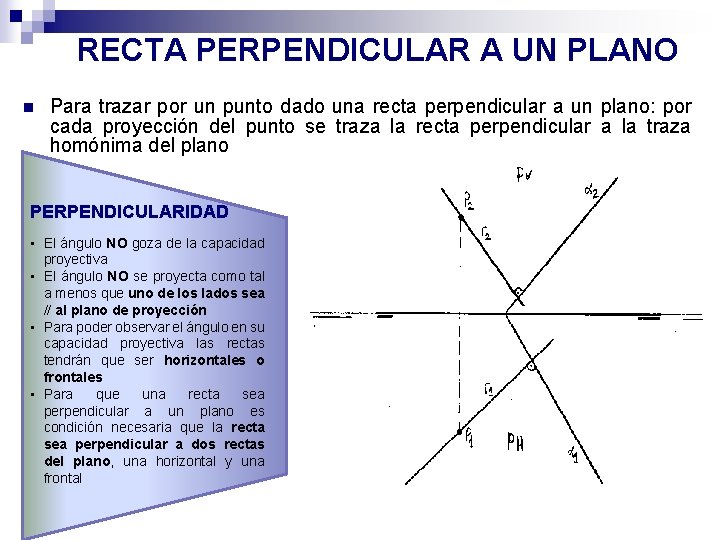
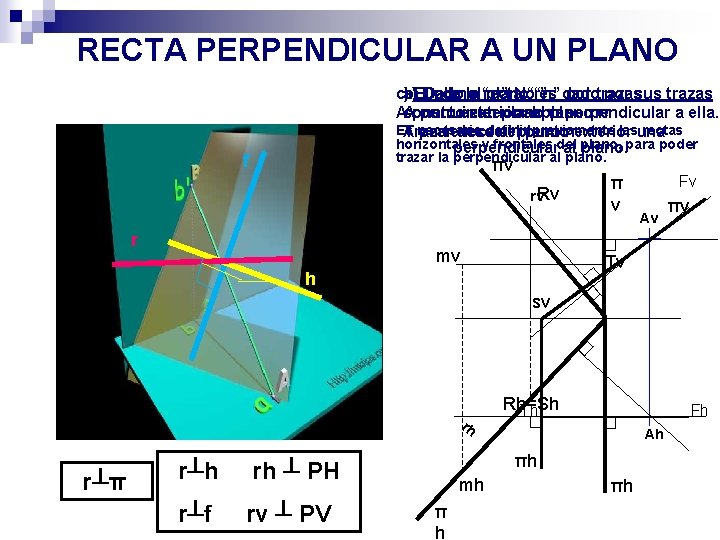
RECTA PERPENDICULAR A UN PLANO n Para trazar por un punto dado una recta perpendicular a un plano: por cada proyección del punto se traza la recta perpendicular a la traza homónima del plano PERPENDICULARIDAD • El ángulo NO goza de la capacidad proyectiva • El ángulo NO se proyecta como tal a menos que uno de los lados sea // al plano de proyección • Para poder observar el ángulo en su capacidad proyectiva las rectas tendrán que ser horizontales o frontales • Para que una recta sea perpendicular a un plano es condición necesaria que la recta sea perpendicular a dos rectas del plano, una horizontal y una frontal

RECTA PERPENDICULAR A UN PLANO c)a) b)El. Dada Dado plano la el“π” recta plano No “r” “π” es dado por trazas por sus trazas Aconstruir Apuntoexterior un plano alalplano π plano perpendicular ππ a ella. Es necesario definir previamente lasuna rectas A Trazar pertenece desde alelplano punto πexterior horizontales y frontales del perpendicular al plano, plano. para poder trazar la perpendicular al plano. f πv rv. Rv r mv π v Fv Av πv Tv h sv rh FIGURA ESPACIAL r┴π r┴h rh ┴ PH r┴f rv ┴ PV Rh=Sh Th Fh Ah πh mh π h πh

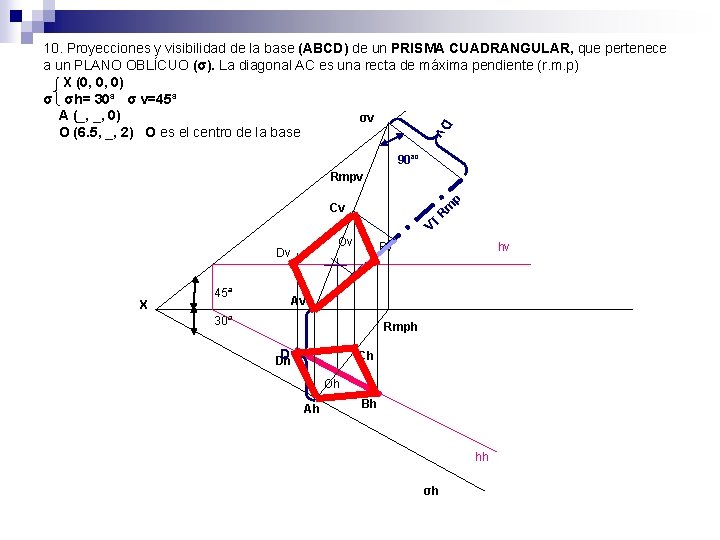
Dv 10. Proyecciones y visibilidad de la base (ABCD) de un PRISMA CUADRANGULAR, que pertenece a un PLANO OBLÍCUO (σ). La diagonal AC es una recta de máxima pendiente (r. m. p) X (0, 0, 0) σ σh= 30ª σ v=45ª A (_, _, 0) σv O (6. 5, _, 2) O es el centro de la base 90ªº p Rmpv VT R m Cv Ov Dv X 45ª Bv hv Av 30ª Rmph Dv Dh Ch Oh Ah Bh hh σh

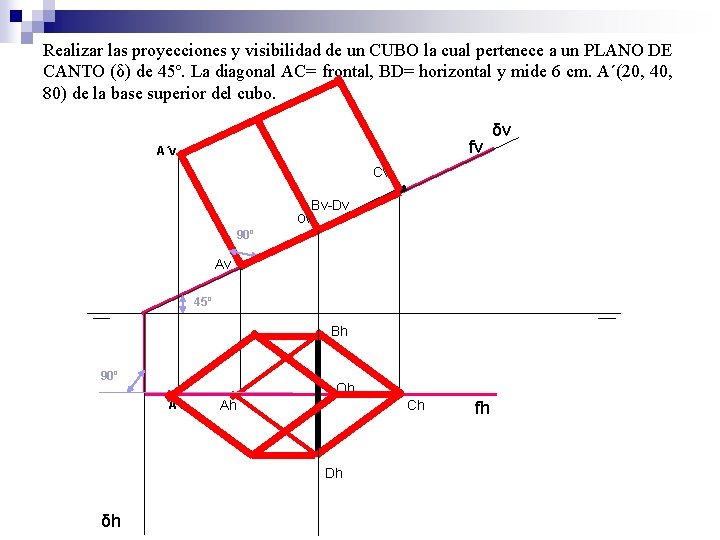
Realizar las proyecciones y visibilidad de un CUBO la cual pertenece a un PLANO DE CANTO (δ) de 45º. La diagonal AC= frontal, BD= horizontal y mide 6 cm. A´(20, 40, 80) de la base superior del cubo. fv A´v Cv Bv-Dv Ov 90º Av 45º Bh 90º Oh A´h Ah Ch Dh δh fh δv

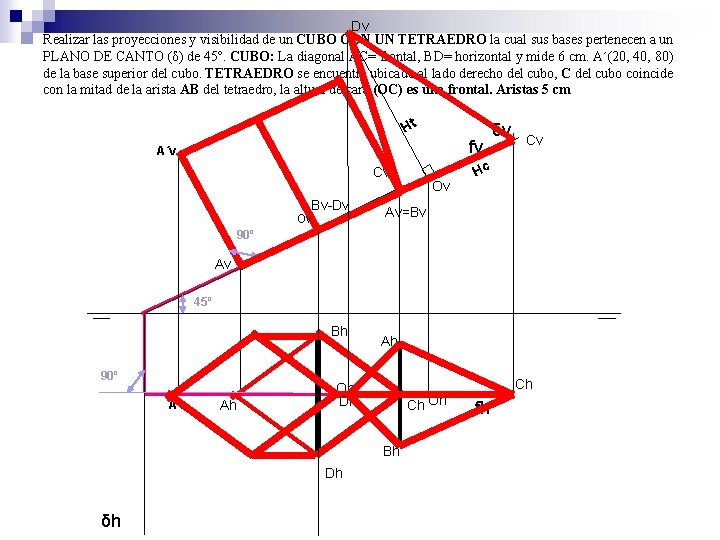
Dv Realizar las proyecciones y visibilidad de un CUBO CON UN TETRAEDRO la cual sus bases pertenecen a un PLANO DE CANTO (δ) de 45º. CUBO: La diagonal AC= frontal, BD= horizontal y mide 6 cm. A´(20, 40, 80) de la base superior del cubo. TETRAEDRO se encuentra ubicado al lado derecho del cubo, C del cubo coincide con la mitad de la arista AB del tetraedro, la altura de cara (OC) es una frontal. Aristas 5 cm Ht fv A´v Cv Bv-Dv Ov Ov δv Cv Hc Av=Bv 90º Av 45º Bh 90º A´h Ah Ah Ch Oh Dh Ch Oh Bh Dh δh fh

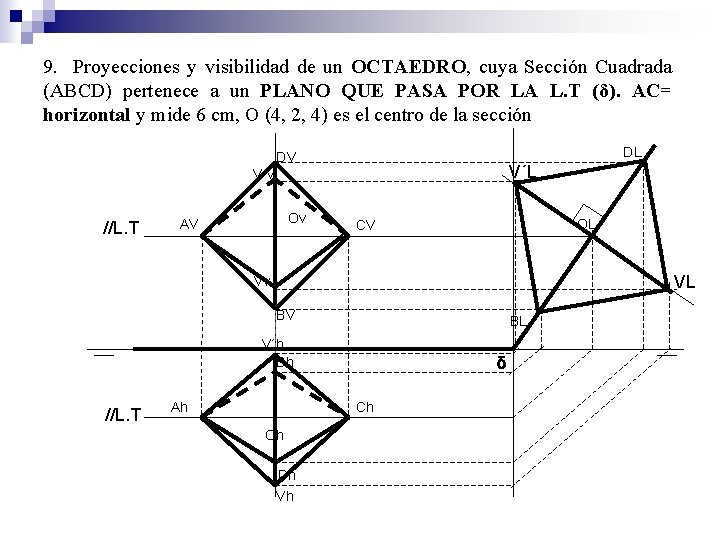
9. Proyecciones y visibilidad de un OCTAEDRO, cuya Sección Cuadrada (ABCD) pertenece a un PLANO QUE PASA POR LA L. T (δ). AC= horizontal y mide 6 cm, O (4, 2, 4) es el centro de la sección DL DV V´L V´v //L. T Ov AV OL CV VL Vv BV BL V´h Bh //L. T Ah δ Ch Oh Dh Vh

5. Proyecciones y visibilidad de una CUÑA cuya base (ABCD) pertenece a un PLANO VERTICAL (λ). Sus diagonales miden 6 cm. AC= frontal, BD= HORIZONTAL. λ X (1, 0, 0) O (5, _ , 3. 5) β=45º. O es el centro de la base. Ev AV λv Fv Ov BV DV CV X β Bh Ah-Ch Oh Fh Dh Eh λh

8. Proyecciones y visibilidad de un PRISMA RECTANGULAR, la base (ABCD) pertenece a un B´v. AC= horizontal que mide 6 cm, BD está contenido en la recta 1 -2 PLANO // L. T (Ω). La diagonal. 1 (3, 0, 6) O´v C´v A´v Ω 2 (8. 2, 5, 0) O´L O (5. 5, _, _) O es el centro de la base D´v La altura del prisma es 6 cm Ωv 1 v Bv Cv Ov Dc Av //L. T V Dv ΩL 2 v 1 h Bh Dc Ch Ah Ov Dh O B´h A´h //L. T h 2 h O´h C´h D´h OL Ωh

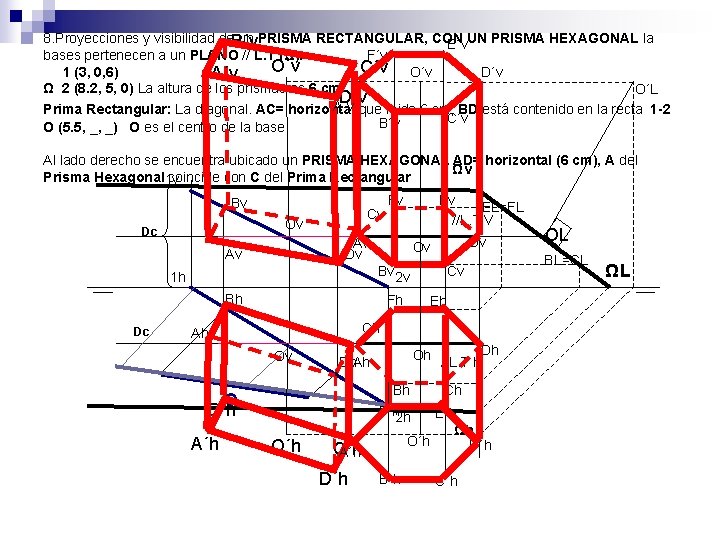
8. Proyecciones y visibilidad de. B´v un PRISMA RECTANGULAR, CON E´v. UN PRISMA HEXAGONAL la bases pertenecen a un PLANO // L. T (Ω). F´v O´v C´v 1 (3, 0, 6) O´v D´v A´v Ω 2 (8. 2, 5, 0) La altura de los prismas es 6 cm O´L D´v A´v que mide 6 cm, BD está contenido en la recta 1 -2 Prima Rectangular: La diagonal. AC= horizontal C´v B´v O (5. 5, _, _) O es el centro de la base Al lado derecho se encuentra ubicado un PRISMA HEXAGONAL AD= horizontal (6 cm), A del Ωv Prisma Hexagonal 1 v coincide con C del Prima Rectangular Bv Cv Ov Dc Ev EL=FL //L. T V Av Dv Av Bh Fh Cv Eh Ch Ah Ov Oh //L. T h. Dh Dh. Ah Bh O B´h A´h Dv Ov Bv 2 v 1 h Dc Fv Ch F´h 2 h O´h E´h Ωh O´h D´h C´h A´h D´h B´h C´h OL BL=CL ΩL