Understand use and prove properties of and relationships

  • Slides: 13
Download presentation
Understand, use and prove properties of and relationships among special quadrilaterals: parallelogram, rectangle, rhombus,

Understand, use and prove properties of and relationships among special quadrilaterals: parallelogram, rectangle, rhombus, square, trapezoid, and kite. MM 1 G 3 D

Vocabulary Parallelogram: A quadrilateral with both pairs of opposite sides parallel. Rhombus: a parallelogram

Vocabulary Parallelogram: A quadrilateral with both pairs of opposite sides parallel. Rhombus: a parallelogram with four congruent sides. Rectangle: a parallelogram with four right angles. Square: a parallelogram with four congruent sides and four right angles.

Corollaries A quadrilateral is a rhombus if and only if it has four congruent

Corollaries A quadrilateral is a rhombus if and only if it has four congruent sides. A quadrilateral is a rectangle if and only if it has four right angles. A quadrilateral is a square if and only if it is a rhombus and a rectangle.

Example 1 Classify the quadrilateral. 7 7 73° 7 7 This quadrilateral is a

Example 1 Classify the quadrilateral. 7 7 73° 7 7 This quadrilateral is a rhombus because all sides are congruent.

Example 2 Classify the quadrilateral. The quadrilateral is a rectangle because all angles are

Example 2 Classify the quadrilateral. The quadrilateral is a rectangle because all angles are right angles. We do not know if it is a square because we do not know if all of the sides are congruent.

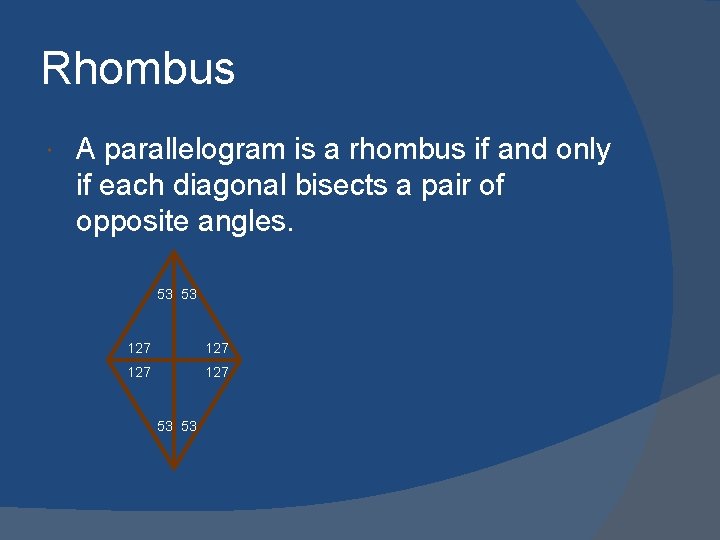
Rhombus A parallelogram is a rhombus if and only if its diagonals are perpendicular.

Rhombus A parallelogram is a rhombus if and only if its diagonals are perpendicular.

Rhombus A parallelogram is a rhombus if and only if each diagonal bisects a

Rhombus A parallelogram is a rhombus if and only if each diagonal bisects a pair of opposite angles. 53 53 127 127 53 53

Rectangle A parallelogram is a rectangle if and only if its diagonals are congruent.

Rectangle A parallelogram is a rectangle if and only if its diagonals are congruent. A B AC is congruent to BD so ABCD is a rectangle. D C

Example 3 The diagonals of rectangle EFGH intersect at T. Given that m<GHF =

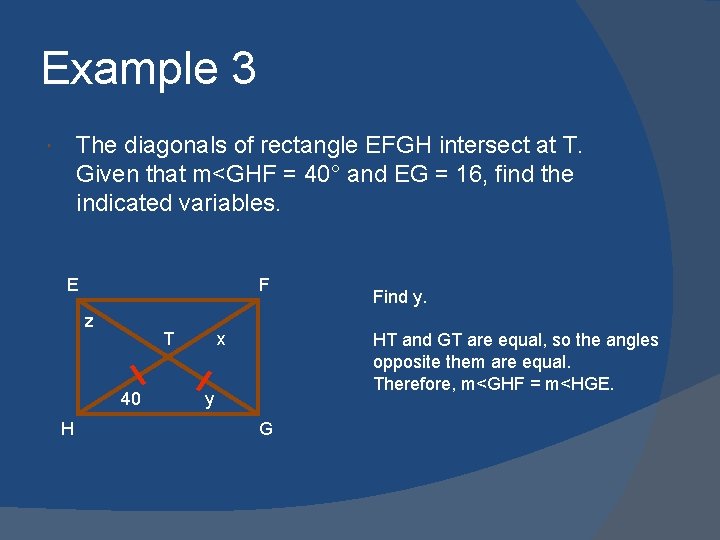
Example 3 The diagonals of rectangle EFGH intersect at T. Given that m<GHF = 40° and EG = 16, find the indicated variables. E F z T x y H G Find x. EFGH is a rectangle so the diagonals are congruent. EG = 16 so FH = 16. EFGH is a parallelogram so the diagonals bisect each other. Therefore, x = FT = 8.

Example 3 The diagonals of rectangle EFGH intersect at T. Given that m<GHF =

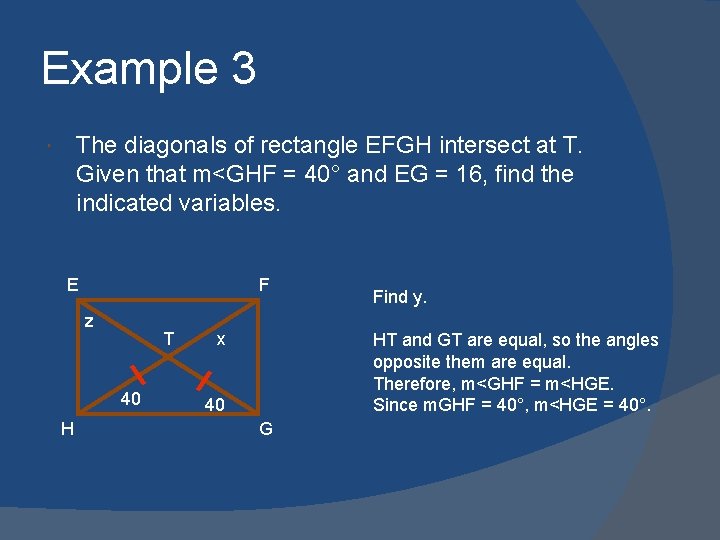
Example 3 The diagonals of rectangle EFGH intersect at T. Given that m<GHF = 40° and EG = 16, find the indicated variables. E F z T 40 H x Find y. HT and GT are equal, so the angles opposite them are equal. Therefore, m<GHF = m<HGE. y G

Example 3 The diagonals of rectangle EFGH intersect at T. Given that m<GHF =

Example 3 The diagonals of rectangle EFGH intersect at T. Given that m<GHF = 40° and EG = 16, find the indicated variables. E F z T 40 H x Find y. HT and GT are equal, so the angles opposite them are equal. Therefore, m<GHF = m<HGE. Since m. GHF = 40°, m<HGE = 40°. 40 G

Example 3 The diagonals of rectangle EFGH intersect at T. Given that m<GHF =

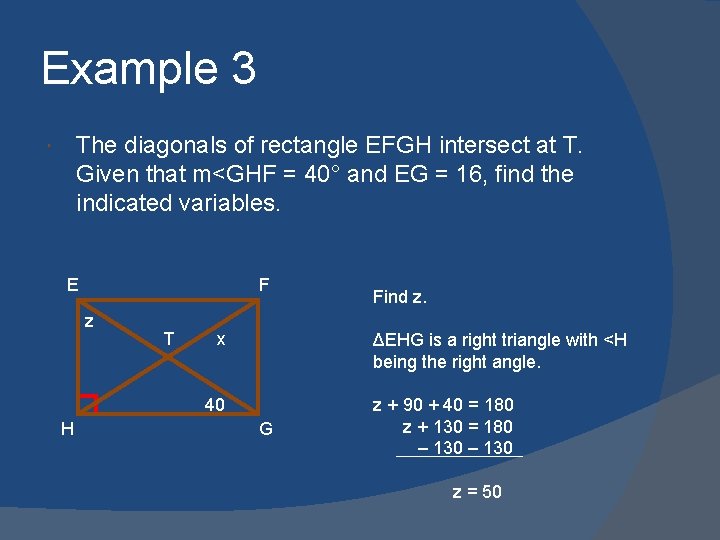
Example 3 The diagonals of rectangle EFGH intersect at T. Given that m<GHF = 40° and EG = 16, find the indicated variables. E F z T x ΔEHG is a right triangle with <H being the right angle. 40 H Find z. G z + 90 + 40 = 180 z + 130 = 180 – 130 z = 50

Assignment Textbook: p. 319 -320 (1 -28)

Assignment Textbook: p. 319 -320 (1 -28)

Materials Properties Electrical properties Magnetic properties Optical propertiesMaterials Properties Electrical properties Magnetic properties Optical properties
Message Properties Messages properties dspacesrcdspacemodulesjspuisrcmainresourcesMessages properties message propertiesMessage Properties Messages properties dspacesrcdspacemodulesjspuisrcmainresourcesMessages properties message properties
Materials Properties Electrical properties Magnetic properties Optical propertiesMaterials Properties Electrical properties Magnetic properties Optical properties
LE PROVE DI DUREZZA 1 INTRODUZIONE Le proveLE PROVE DI DUREZZA 1 INTRODUZIONE Le prove
Confronto esiti prove dingresso e prove quadrimestrali dIstitutoConfronto esiti prove dingresso e prove quadrimestrali dIstituto
Prove Meccaniche Propriet meccaniche Prove meccaniche prova diProve Meccaniche Propriet meccaniche Prove meccaniche prova di
e Prove Basics q The e Prove platforme Prove Basics q The e Prove platform
PROVE FACILI PROVE DIFFICILI Unimmagine del 1995 dalPROVE FACILI PROVE DIFFICILI Unimmagine del 1995 dal
ESITI PROVE INVALSI 2013 14 ESITI PROVE INVALSIESITI PROVE INVALSI 2013 14 ESITI PROVE INVALSI
Le prove dellevoluzione Prove a favore dellevoluzione ILe prove dellevoluzione Prove a favore dellevoluzione I
Confronto esiti prove dingresso TITLE e prove LOREMConfronto esiti prove dingresso TITLE e prove LOREM
Prove Triangles Congruent by SSS Prove Triangles CongruentProve Triangles Congruent by SSS Prove Triangles Congruent