Trees CSE 2011 Winter 2011 12262021 1 Trees

Trees CSE 2011 Winter 2011 12/26/2021 1

Trees l Linear access time of linked lists is prohibitive ¡Does there exist any simple data structure for which the running time of most operations (search, insert, delete) is O(log N)? l Trees ¡Basic concepts ¡Tree traversal ¡Binary trees ¡Binary search trees ¡AVL trees 2

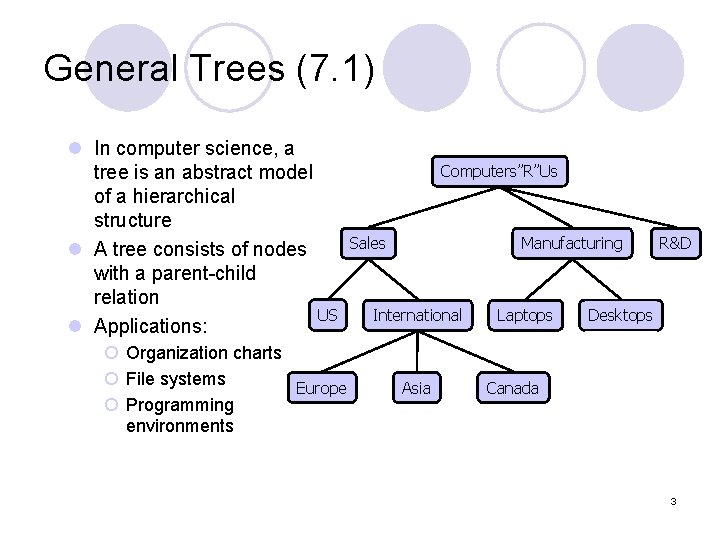
General Trees (7. 1) l In computer science, a tree is an abstract model of a hierarchical structure l A tree consists of nodes with a parent-child relation US l Applications: ¡ Organization charts ¡ File systems Europe ¡ Programming environments Computers”R”Us Sales Manufacturing International Asia Laptops R&D Desktops Canada 3

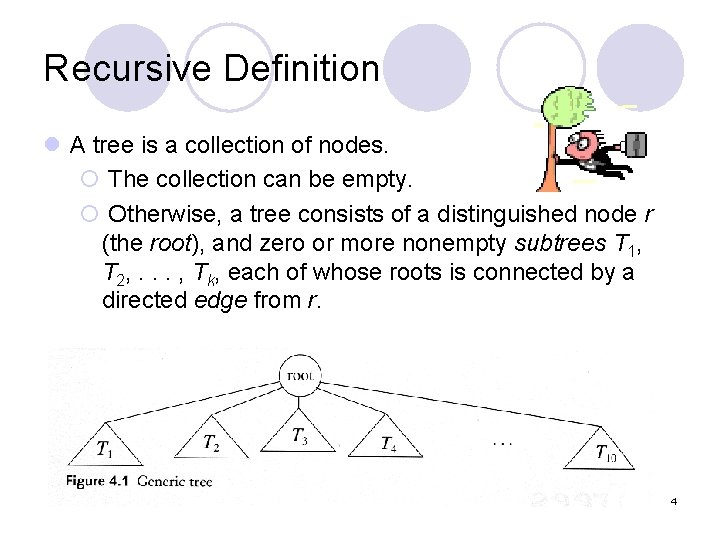
Recursive Definition l A tree is a collection of nodes. ¡ The collection can be empty. ¡ Otherwise, a tree consists of a distinguished node r (the root), and zero or more nonempty subtrees T 1, T 2, . . . , Tk, each of whose roots is connected by a directed edge from r. 4

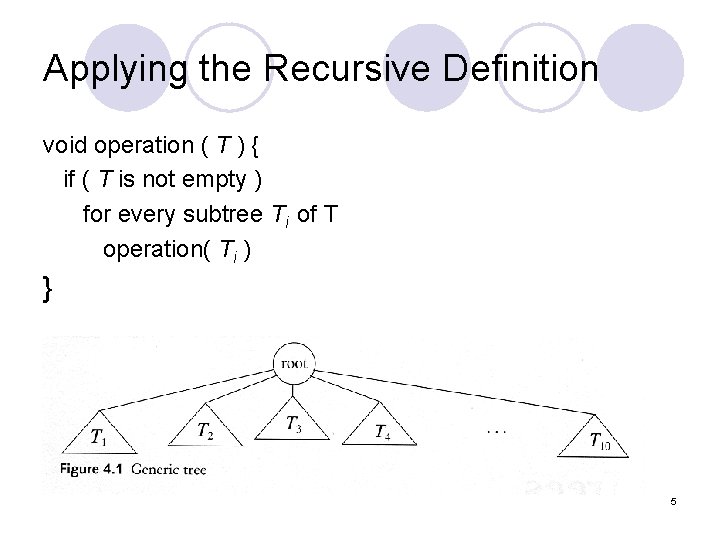
Applying the Recursive Definition void operation ( T ) { if ( T is not empty ) for every subtree Ti of T operation( Ti ) } 5

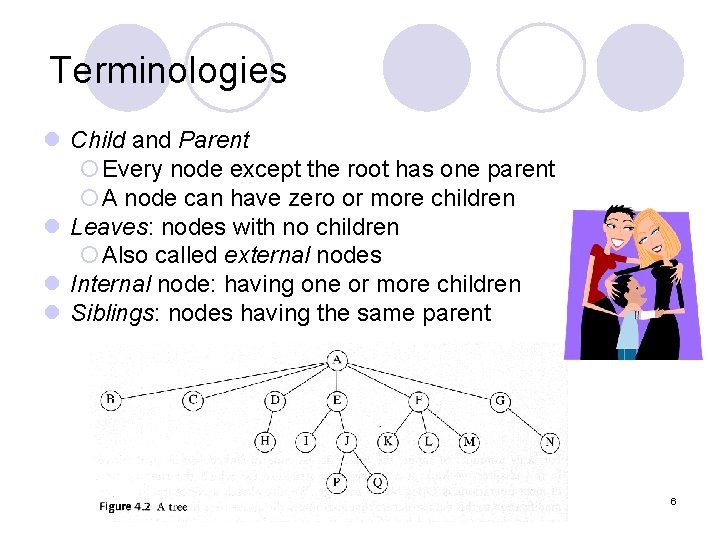
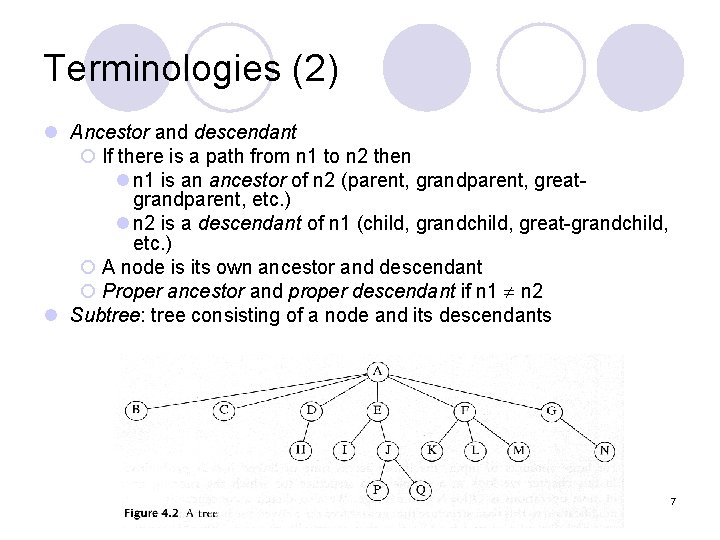
Terminologies l Child and Parent ¡Every node except the root has one parent ¡A node can have zero or more children l Leaves: nodes with no children ¡Also called external nodes l Internal node: having one or more children l Siblings: nodes having the same parent 6

Terminologies (2) l Ancestor and descendant ¡ If there is a path from n 1 to n 2 then l n 1 is an ancestor of n 2 (parent, grandparent, greatgrandparent, etc. ) l n 2 is a descendant of n 1 (child, grandchild, great-grandchild, etc. ) ¡ A node is its own ancestor and descendant ¡ Proper ancestor and proper descendant if n 1 n 2 l Subtree: tree consisting of a node and its descendants 7

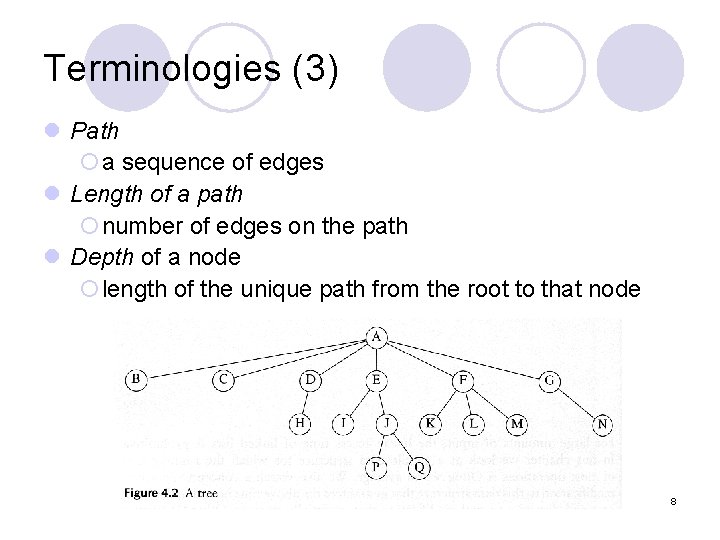
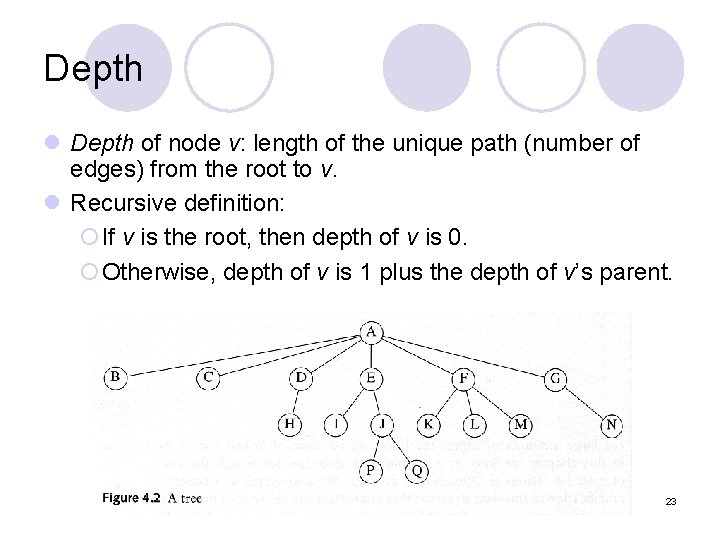
Terminologies (3) l Path ¡a sequence of edges l Length of a path ¡number of edges on the path l Depth of a node ¡length of the unique path from the root to that node 8

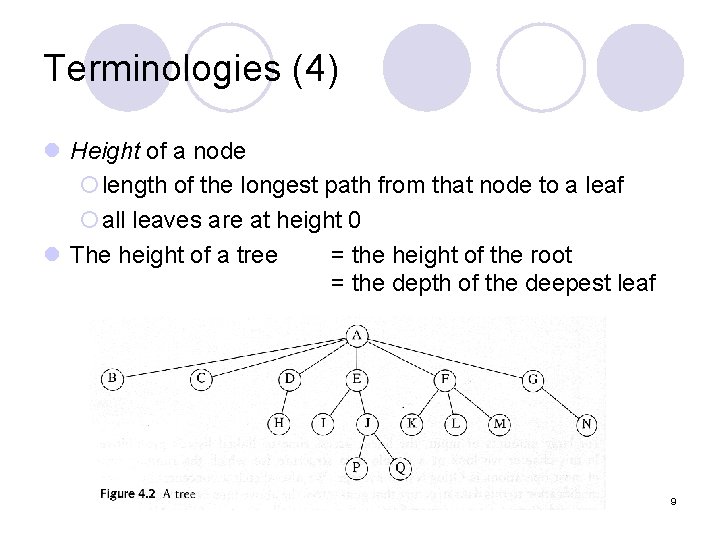
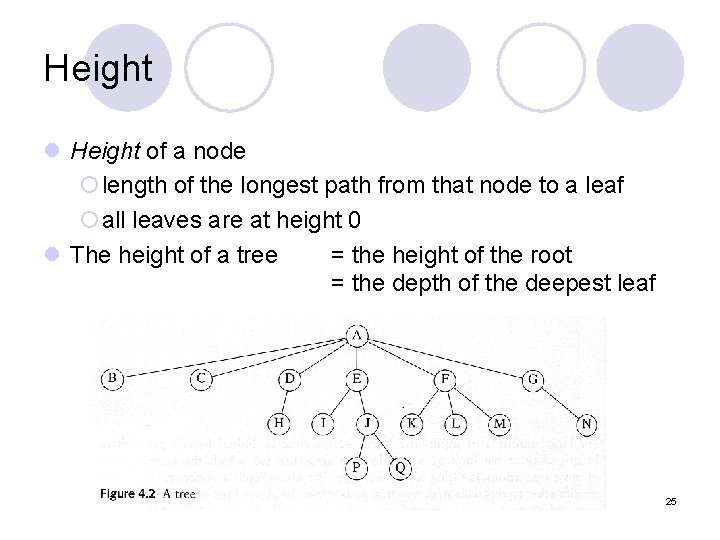
Terminologies (4) l Height of a node ¡length of the longest path from that node to a leaf ¡all leaves are at height 0 l The height of a tree = the height of the root = the depth of the deepest leaf 9

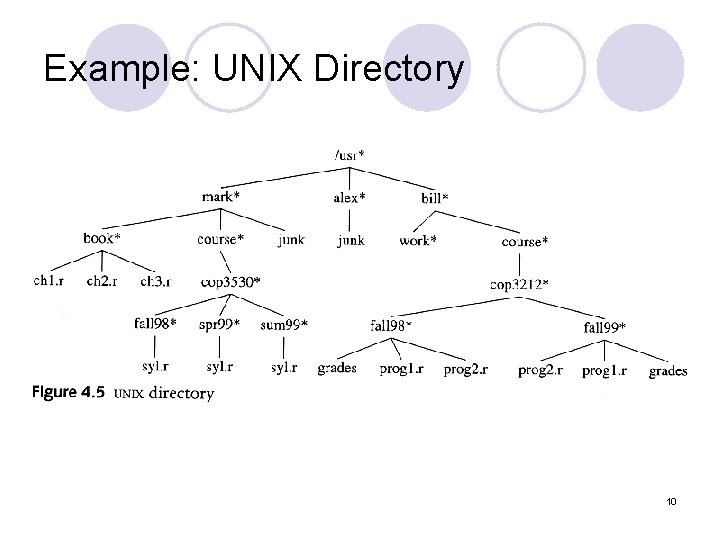
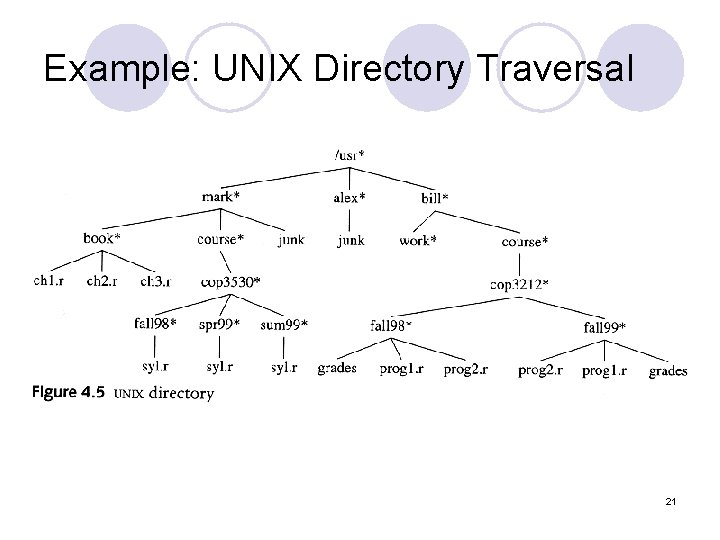
Example: UNIX Directory 10

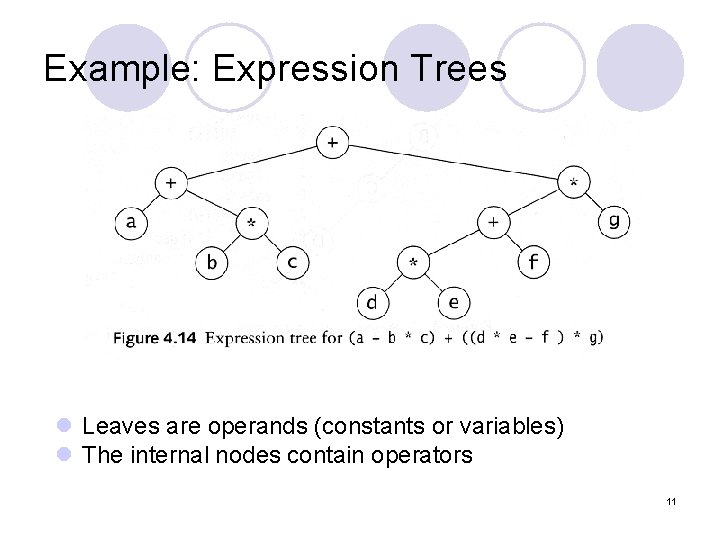
Example: Expression Trees l Leaves are operands (constants or variables) l The internal nodes contain operators 11

Tree ADT o Query methods: l We use positions to abstract nodes (position node) l Generic methods: ¡ ¡ n n integer size() boolean is. Empty() Iterator elements() position. Iterator positions() n boolean is. Internal(p) boolean is. External(p) boolean is. Root(p) o Update method: n l Accessor methods: object replace (p, e): replace with e and return element stored at node p o Additional update methods ¡ position root() ¡ position parent(p) ¡ position. Iterator children(p) may be defined by data structures implementing the Tree ADT Trees 12

Implementing Trees l Arrays ? l Linked “lists” (pointers) ? 13

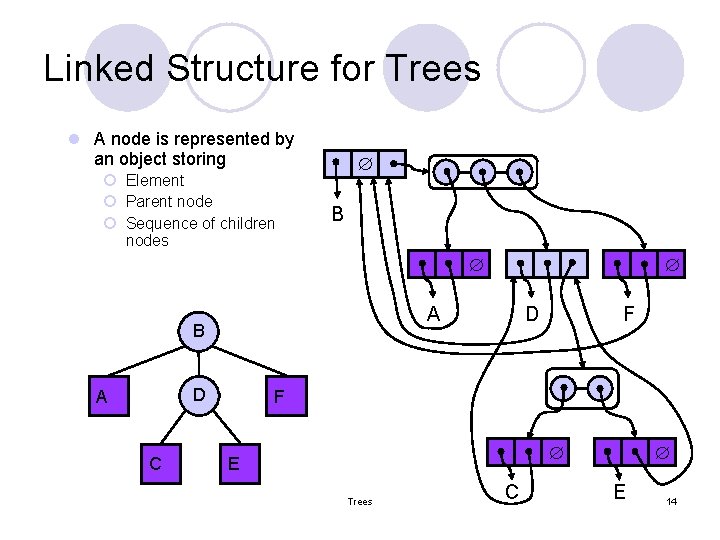
Linked Structure for Trees l A node is represented by an object storing ¡ Element ¡ Parent node ¡ Sequence of children nodes B A B D A C D F F E Trees C E 14

Tree Traversal Algorithms (7. 2) l Preorder ¡Visit v first ¡Then visit the descendants of v l Postorder ¡Visit the descendants of v first ¡Then visit v last l Depth and Height 15

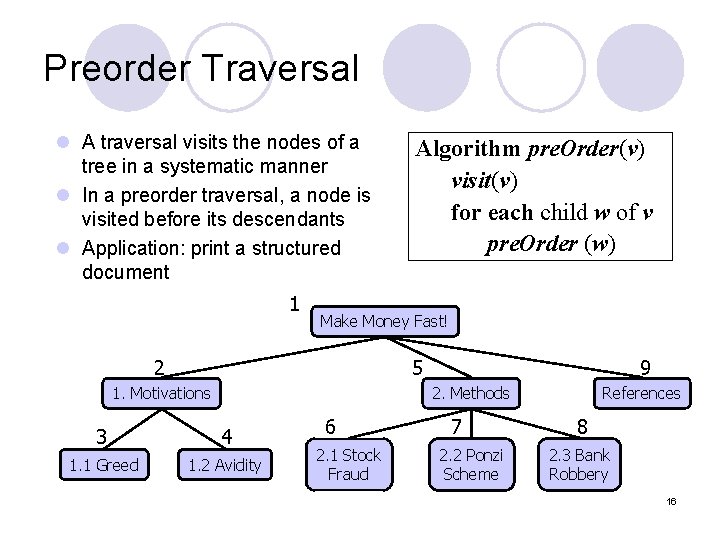
Preorder Traversal l A traversal visits the nodes of a tree in a systematic manner l In a preorder traversal, a node is visited before its descendants l Application: print a structured document 1 Algorithm pre. Order(v) visit(v) for each child w of v pre. Order (w) Make Money Fast! 2 5 1. Motivations 9 2. Methods 3 4 1. 1 Greed 1. 2 Avidity 6 2. 1 Stock Fraud 7 2. 2 Ponzi Scheme References 8 2. 3 Bank Robbery 16

An Example 17

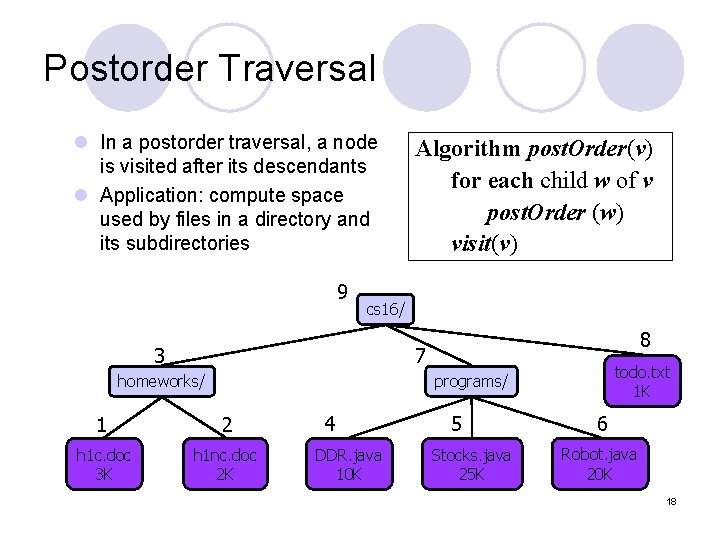
Postorder Traversal l In a postorder traversal, a node is visited after its descendants l Application: compute space used by files in a directory and its subdirectories 9 Algorithm post. Order(v) for each child w of v post. Order (w) visit(v) cs 16/ 3 8 7 homeworks/ todo. txt 1 K programs/ 1 2 h 1 c. doc 3 K h 1 nc. doc 2 K 4 DDR. java 10 K 5 Stocks. java 25 K 6 Robot. java 20 K 18

Applications l Either preorder traversal or postorder traversal can be used when the order of computation is not important. Example: printing the contents of a tree (in any order) l Preorder traversal is required when we must perform a computation for each node before performing any computations for its descendents. Example: Printing the headings of chapters, sections, sub-sections of a book. l Postorder traversal is needed when the computation for a node v requires the computations for v’s children to be done first. Example: Given a file system, compute the disk space used by a directory. 19

Example: Computing Disk Space 20

Example: UNIX Directory Traversal 21

Example: Unix Directory Traversal Preorder Postorder 22

Depth l Depth of node v: length of the unique path (number of edges) from the root to v. l Recursive definition: ¡If v is the root, then depth of v is 0. ¡Otherwise, depth of v is 1 plus the depth of v’s parent. 23

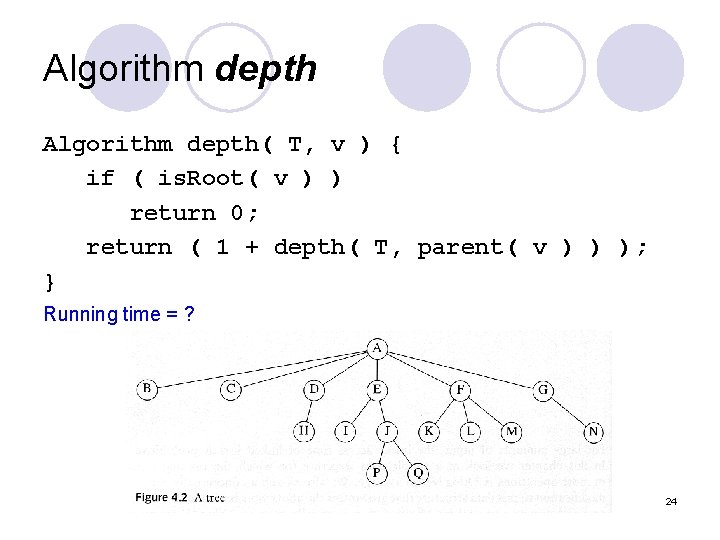
Algorithm depth( T, v ) { if ( is. Root( v ) ) return 0; return ( 1 + depth( T, parent( v ) ) ); } Running time = ? 24

Height l Height of a node ¡length of the longest path from that node to a leaf ¡all leaves are at height 0 l The height of a tree = the height of the root = the depth of the deepest leaf 25

Computing the Height of a Tree l The height of a tree = the depth of the deepest leaf Algorithm height( T ) { h = 0; for every node v in T if( is. External( v ) ) h = max( h, depth( T, v ) ); } Running time: O(n) + Σv(dv + 1) for all external nodes v Σv dv = O(n 2) in the worst case not efficient 26

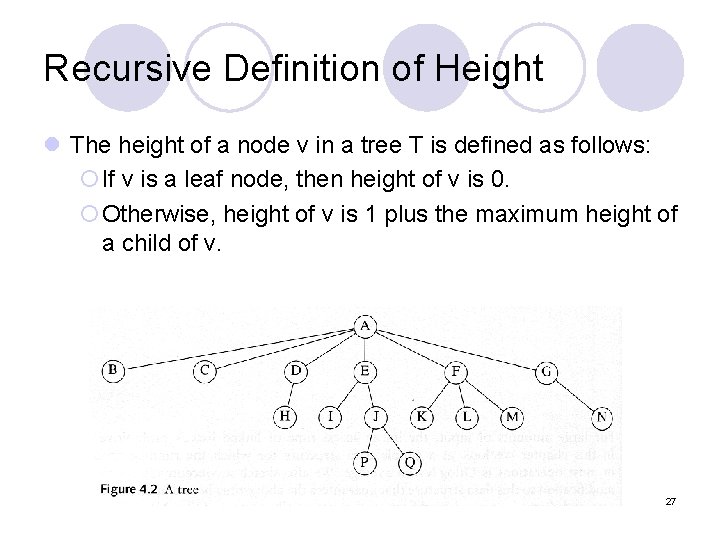
Recursive Definition of Height l The height of a node v in a tree T is defined as follows: ¡If v is a leaf node, then height of v is 0. ¡Otherwise, height of v is 1 plus the maximum height of a child of v. 27

Algorithm height 2( T, v ) { if ( is. External( v ) ) return 0; h = 0; for every child w of v h = max( h, height 2( T, w ) ); return( 1 + h ); } l Height of the tree: H = height 2( T, root ); l Running time: Σv(cv + 1) O( ? ) l We visit each node exactly once. 28

Next time … l Binary Trees (7. 3) l Binary Search Trees (10. 1) 29