Tractament de Dades Experimentals Errors experimentals Propagaci derrors

Tractament de Dades Experimentals • • • Errors experimentals Propagació d'errors Expressió d'un resultat experimental Error d'una magnitud en funció d'altres Resum per calcular errors Ajust d'una recta § § Procediment gràfic Regressió lineal (amb Excel) © 2013 Quim Trullàs Aquestes transparències es poden utilitzar amb fins educatius no comercials, sempre que s'indiqui l'autoria These transparencies may be used for educational non-commercial purposes so long as the source is attributed

Errors experimentals Quan mesurem una determinada magnitud (voltatge, intensitat, . . . ), el resultat no és un valor exacte, sinó un interval al voltant d'un valor aproximat. El resultat de la mesura s'acostuma a escriure - x és el valor del resultat de la mesura que es considera millor - x és l'error de x L'error relatiu es defineix com Tot aparell de mesura té un error de resolució que depèn de si l'aparell és • • analògic digital © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 2

Aparells analògics Resolució: diferència entre dos valors consecutius de l'escala Error de resolució = Resolució/2 A l'exemple la resolució és de 0. 2 A La intensitat mesurada, I , està en l'interval 4. 2 A < I < 4. 4 A I = 4. 3 A L'error de la mesura és I = Resolució/2 = (0. 2 A)/2 = 0. 1 A I = 4. 3 A 0. 1 A = (4. 3 0. 1) A rel, I = 0. 1/4. 3 = 0. 024 2. 4% Aparells digitals Resolució: una unitat de l'últim dígit Error de resolució = Resolució A l'exemple la resolució és de 0. 001 A I = 0. 198 A L'error de la mesura és I = Resolució = 0. 001 A I = (0. 198 0. 001) A = (198 1) 10 -3 A = (198 1) m. A rel, I = 1/198 = 0. 005 0. 5% © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 3

Propagació d'errors No totes les magnituds es poden mesurar directament. Exemple: L'àrea d'un cercle, A, es determina a partir del seu diàmetre D, Si una magnitud z és funció d'una altra magnitud x, z(x) , quan calculem el valor de z a partir de la mesura directa, x x , z z. l'error de x és propaga a la mesura indirecta de z, z(x) z(xo+ x) z(xo) Si z'(xo) = a xo Taylor: z(x) z(xo) + z'(xo)·(x-xo) z(xo+ x) z(xo) + z'(xo) x z(xo- x) z(xo) - z'(xo) x x xo- x xo © 2013 Quim Trullàs (UPC) xo+ x L'error estimat de z és Tractament de Dades Experimentals 4

Exemple: Quina és l'àrea d'un cercle de diàmetre D = (12. 5 0. 5) mm? (12. 5 mm)2/4 = 122. 71846 mm 2 Té sentit escriure (122. 71846 9. 817477) mm 2 ? ? ? © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 5

Expressió d'un resultat experimental Té sentit escriure (122. 71846 9. 817477) mm 2 ? ? És absurd donar la magnitud amb 4 decimals si l'error és de l'ordre de 10 També és absurd donar un error amb tants dígits Hem de suprimir xifres. Ho podem fer de tres maneres: a) Aproximació per defecte o truncament Suprimir les xifres sobrants Exemple si no volem decimals 42. 984 42 ; 42. 373 42 ; 42. 500 42 b) Aproximació per excés Suprimir les xifres sobrants i sumar una unitat a l'última xifra expressada Exemple si no volem decimals 42. 984 43 ; 42. 373 43 ; 42. 500 43 c) Arrodoniment Truncar o aproximar per excés d'acord amb el criteri següent: - Si la xifra d'ordre més alt suprimida és inferior a 5, es trunca - Si la xifra d'ordre més alt suprimida és superior o igual a 5, s'aproxima per excés Exemple si no volem decimals 42. 984 43 ; 42. 373 42 ; 42. 500 43 © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 6

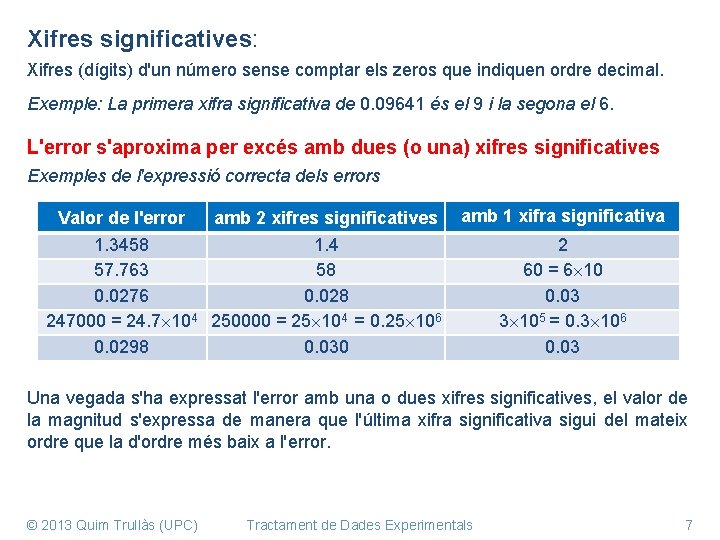
Xifres significatives: Xifres (dígits) d'un número sense comptar els zeros que indiquen ordre decimal. Exemple: La primera xifra significativa de 0. 09641 és el 9 i la segona el 6. L'error s'aproxima per excés amb dues (o una) xifres significatives Exemples de l'expressió correcta dels errors Valor de l'error amb 2 xifres significatives 1. 3458 1. 4 57. 763 58 0. 0276 0. 028 247000 = 24. 7 104 250000 = 25 104 = 0. 25 106 0. 0298 0. 030 amb 1 xifra significativa 2 60 = 6 10 0. 03 3 105 = 0. 3 106 0. 03 Una vegada s'ha expressat l'error amb una o dues xifres significatives, el valor de la magnitud s'expressa de manera que l'última xifra significativa sigui del mateix ordre que la d'ordre més baix a l'error. © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 7

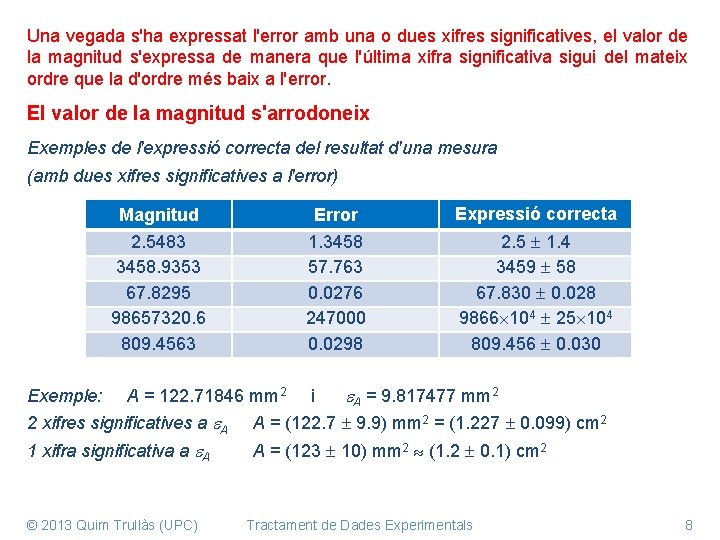
Una vegada s'ha expressat l'error amb una o dues xifres significatives, el valor de la magnitud s'expressa de manera que l'última xifra significativa sigui del mateix ordre que la d'ordre més baix a l'error. El valor de la magnitud s'arrodoneix Exemples de l'expressió correcta del resultat d'una mesura (amb dues xifres significatives a l'error) Magnitud 2. 5483 3458. 9353 67. 8295 98657320. 6 809. 4563 Error 1. 3458 57. 763 0. 0276 247000 0. 0298 Expressió correcta 2. 5 1. 4 3459 58 67. 830 0. 028 9866 104 25 104 809. 456 0. 030 Exemple: A = 122. 71846 mm 2 i A = 9. 817477 mm 2 2 xifres significatives a A A = (122. 7 9. 9) mm 2 = (1. 227 0. 099) cm 2 1 xifra significativa a A A = (123 10) mm 2 (1. 2 0. 1) cm 2 © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 8

Error d'una magnitud funció d'altres Si z depèn de més d'una magnitud z(x 1, . . . , xi, . . . , x. N) amb el seu error z és la mitjana quadràtica dels errors que produirien cadascuna de les variables ( ) per separat suposant que les altres són constants. Cada ( ) produeix un (i = 1, . . , N) i l'error propagat a z és la derivada parcial de z respecte xi , és a dir, derivar z respecte xi com si les altres variables fossin constants. En el cas d'una magnitud que depèn de dues variables, z(x, y), i Exemple: z = ax - by © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 9

Errors de magnituds que són productes i quocients En els dos casos particulars z(x) = ax i z(y) = a/y on a és constant, i pot ser a = 1, z = ax z = a/y En el cas d'una magnitud z que depèn de dues variables x i y de la forma z = bxy o z = bx/y © 2013 Quim Trullàs (UPC) i Tractament de Dades Experimentals 10

Resum per calcular errors ●En els aparells analògics es considera que l'error de resolució és igual a la meitat de la diferència entre dos valors consecutius de l'escala. ●En els aparells digitals es considera que l'error de resolució és igual a unitat en l'últim dígit. ● El resultat de la mesura s'acostuma a escriure x x x és el resultat de la mesura que es considera millor i x és un nombre real positiu (amb les mateixes unitats que x) anomenat error absolut. ● L'error relatiu es defineix com ● L'error estimat de z(x) és Exemples: z = ax z = a/y on a és una constant que pot ser a = 1 © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 11

● L'error estimat de z(x, y), és la mitjana quadràtica de l'error que produiria x, z(x), i el que produiria y, z(y), suposant que l'altra variable és constant. Exemple: z = ax - by ● En el cas de les magnituds que s'expressen com productes i quocients z = ax o z = a/y on a és una constant que pot ser a = 1 ● L'ERROR S'APROXIMA PER EXCÉS a 2 (o 1) xifres significatives. ● EL VALOR DE LA MAGNITUD S'ARRODONEIX, de manera que l'última xifra significativa sigui del mateix ordre que la d'ordre més baix a l'error. © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 12

Ajust d'una recta Exemple: La resistivitat d'un material canvia amb la temperatura T segons = a. T + 0 on a i 0 són constants Per determinar els valors de a i 0 cal mesurar a diferents T. Si mesurem per a N valors diferents de T tindrem un N parells de valors (Ti, i). Teòricament aquests punts haurien d'estar sobre la recta = a. T + 0. A la pràctica, però, com a conseqüència dels errors en les mesures de T i , els punts no estan perfectament alineats. N i 2 1 T T 1 © 2013 Quim Trullàs (UPC) T 2 Ti Tractament de Dades Experimentals TN 13

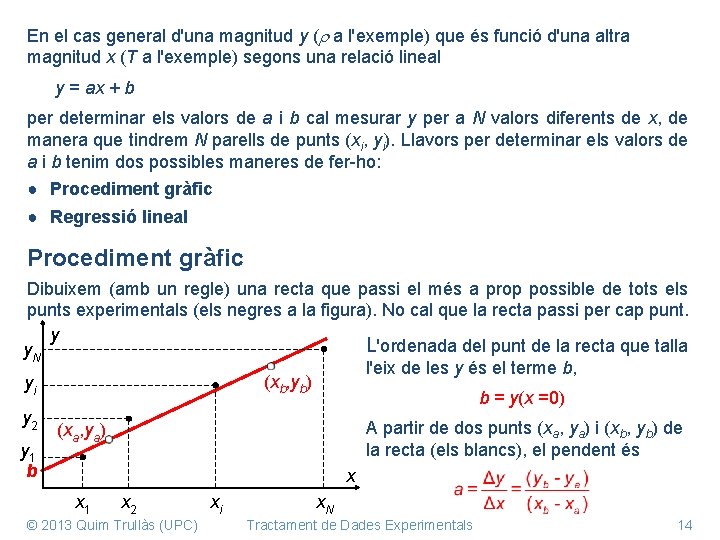
En el cas general d'una magnitud y ( a l'exemple) que és funció d'una altra magnitud x (T a l'exemple) segons una relació lineal y = ax + b per determinar els valors de a i b cal mesurar y per a N valors diferents de x, de manera que tindrem N parells de punts (xi, yi). Llavors per determinar els valors de a i b tenim dos possibles maneres de fer-ho: ● Procediment gràfic ● Regressió lineal Procediment gràfic Dibuixem (amb un regle) una recta que passi el més a prop possible de tots els punts experimentals (els negres a la figura). No cal que la recta passi per cap punt. y L'ordenada del punt de la recta que talla y. N l'eix de les y és el terme b, (x , y ) yi b b b = y(x =0) y 2 A partir de dos punts (xa, ya) i (xb, yb) de (xa, ya) la recta (els blancs), el pendent és y 1 b x x 1 x 2 xi x. N © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 14

Regressió lineal Matemàticament, amb mètode dels mínims quadrats, que consisteix a fer mínima la suma dels quadrats de les diferències entre l'ordenada del punt experimental i la corresponent a la recta ajustada per a la mateixa abscissa es demostra que La recta que s'obté amb aquests paràmetres a i b, s'anomena recta de regressió, que la podem pintar a partir de dos punts per dos valors de x, xa i xb y. N (xa, ya=axa+b) y (xb, yb=axb+b) (xb, yb) yi y 2 y 1 (xa, ya) x x 1 x 2 © 2013 Quim Trullàs (UPC) xi x. N Tractament de Dades Experimentals 15

L'Excel (97) permet fer la regressió lineal (Apèndix D) • • A les columnes A i B introduïm els valors de x i y. Marquem els valors de les columnees A i B. Cliquem la icona "Asistente para gráficos" /º Triem el tipus de gràfic "XY (Dispersión)" subtipus "Dispersión con puntos de datos conectados por lineas suavizadas". Cliqueu un punt i quedaran tots seleccionats. Premeu el botó dret del ratolí i trieu "agregar linea de tendencia" (lineal). A "opciones" marqueu "Presentar ecuación en el gráfico" Excel 2010 Insertar Dispersión Agregar línea de tendencia (lineal) Presentar ecuación en el gráfico © 2013 Quim Trullàs (UPC) Tractament de Dades Experimentals 16