Thorme des restes chinois Ce projet est ralise

Théorème des restes chinois Ce projet est réalise par : Dini Ahmed Mohamed Ibrahim Abdallah Ali

Citation << Une oeuvre où il y a des théories est comme un objet sur lequel on laisse la marque du prix >> Marcel Proust

Organisation Dans un premier temps, nous présenterons la résolution mathématique du problème des congruences simultanées avec des différents Méthodes , d’abord dans la situation la plus simple où les modules sont premiers entre eux deux à deux, puis dans un cadre général. Dans un seconde temps, nous établirons une résolution informatique du problème des congruences simultanées dans des différents langages (C++, JAVA SCRIPT).

Sommaire I PARTIE MATHEMATIQUE I) BREF INTRODUCTION II) DEMONSTRATION DU THEOREME III) QUELQUES APPLICATIONS II PARTIE INFORMATIQUE I) Base de Java II) Algorithme III) Langage Java IV)Exécution Des Exemple à partir du Langage Java IV) ASTUCES ET METHODES V) COMPARAISON DES DIFFERENTS METHODES V) Exécution Des Exemple à partir du Langage C++ VI) CAS PARTICULIER VI) Exécution Des Exemple à partir du Langage Java. Script

I) Bref Introduction Par son histoire et sa religion, la chine a toujours mis l’accent sur l’astronomie. Ainsi, dans le but de prévoir des dates ou événements astronomiques, les astronomes chinois ont découverts le théorème des restes chinois. D’après certains textes, on peut évaluer l’apparition du théorème au 3ème siècle. Le théorème a évolué au cours du temps sous diverses formes et avec l’apparition de nouveaux, dérivés du théorème initial. Ce théorème, permettant de calculer des systèmes de congruences

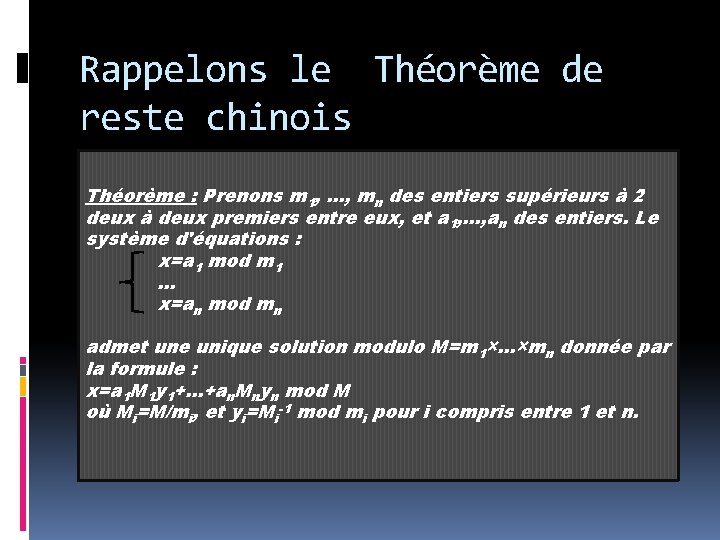
Rappelons le Théorème de reste chinois Théorème : Prenons m 1, . . . , mn des entiers supérieurs à 2 deux à deux premiers entre eux, et a 1, . . . , an des entiers. Le système d'équations : x=a 1 mod m 1. . . x=an mod mn admet une unique solution modulo M=m 1×. . . ×mn donnée par la formule : x=a 1 M 1 y 1+. . . +an. Mnyn mod M où Mi=M/mi, et yi=Mi-1 mod mi pour i compris entre 1 et n.

II)Démonstration du Théorème Prouvons d’abord l’existence d’une solution. Pour tout 1< i < n, on pose Mi = M/mi On pose x = a 1*M 1*x 1 + a 2*M 2* x 2 +. . + an*Mn*xn Montrons que x constitue une solution du système de congruences Prouvons ensuite l’unicité de la solution modulo M. Soient x et x′ deux solutions du système de congruences Montrons que x ≡ x′ mod M.

Quelques Applications SYSTEME X ≡ 3 mod 11 X ≡ 6 mod 8 X ≡ -1 mod 15 PROBLEME Combien l'armée de Han Xing comporte-telle de soldats si, rangés par 3 colonnes, il reste deux soldats, rangés par 5 colonnes, il reste trois soldats et, rangés par 7 colonnes, il reste deux soldats ?

III) Les Différents Méthodes Soit le Système : X ≡ 3 mod 11 X ≡ 6 mod 8 X ≡ -1 mod 15 Pour résoudre ce système utilisons les Méthodes A et B

Application direct

Première Méthode : A X ≡ 1 mod 11 X ≡ 0 mod 8 X ≡ 0 mod 15 Avec l’identité de Bézout On obtient donc X 1 =-120 X ≡ 0 mod 11 X ≡ 1 mod 8 X ≡ 0 mod 15 Avec x 2 = -495 X ≡ 0 mod 11 X ≡ 0 mod 8 X ≡ 1 mod 15 AVEC X 3= 616 Finalement on obtient X = 3 x 1 +6 x 2 –x 3 = - 3946 On rajoute a – 3946 des multiples de M= 8*11*15 = 1320 D’où : X’ = - 3946+ 3*1320 = 14

Seconde Méthode : B X ≡ 3 mod 11 X ≡ 6 mod 8 En Cherchant T et U tels que : 3+11 T= 6+8 U OU Par le même procède on obtient donc la solution recherche Avec X= 11 T-8 U = 3 On peut résoudre ceci par l algorithme d’Euclide et par Bézout mais ici, on constate que T=U= 1 est une solution 14 mod 1320

Pour résoudre le problème utilisons la méthode c Combien l'armée de Han Xing comporte -t-elle de soldats si, rangés par 3 colonnes, il reste deux soldats, rangés par 5 colonnes, il reste trois soldats et, rangés par 7 colonnes, il reste deux soldats ?

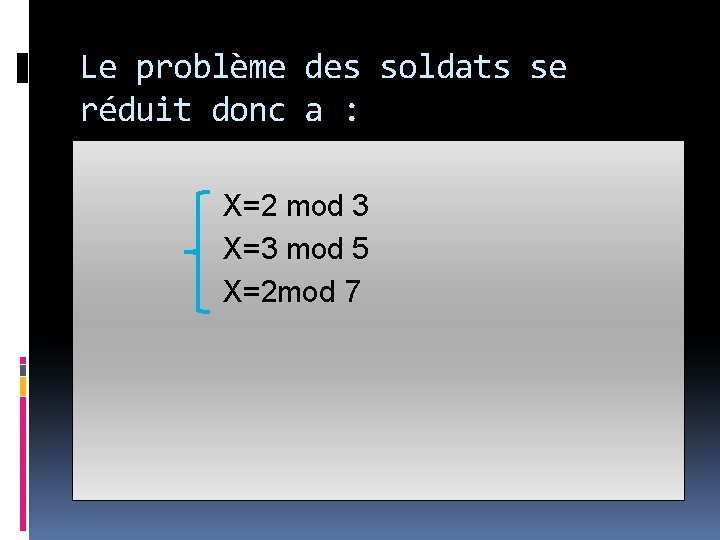
Le problème des soldats se réduit donc a : X=2 mod 3 X=3 mod 5 X=2 mod 7

Application direct

ZERO METHODE Règle : « En comptant par trois, il en reste deux » : poser 140. « En comptant par cinq, il en reste trois » : poser 63. « En comptant par sept, il en reste deux » : poser 30. Faire la somme de ces trois nombres, obtenir 233. Soustraire 210 de ce total, d’où la réponse. Reponse : 23 En général, pour chaque unité restante d’un décompte par trois, poser 70 ; pour chaque unité restante d’un décompte par 5, poser 21 ; pour chaque unité restante d’un décompte par 7, poser 15. Si [la somme ainsi obtenue] vaut 106 ou plus, ôter 105 pour trouver la réponse

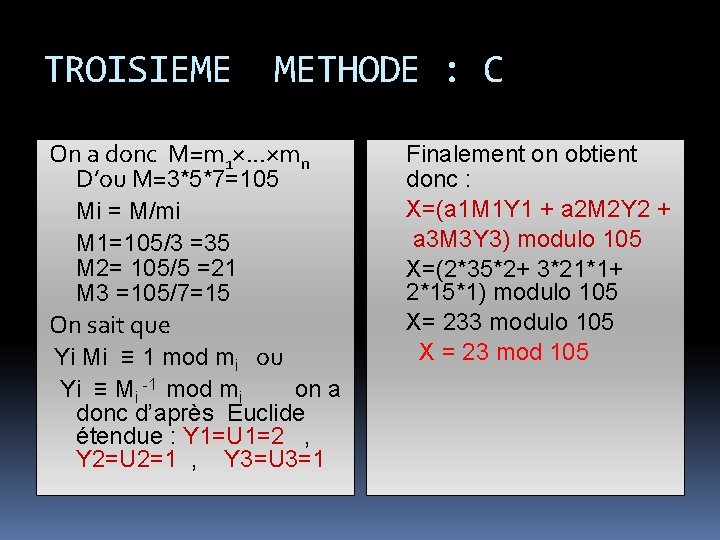
TROISIEME METHODE : C On a donc M=m 1×. . . ×mn D’ou M=3*5*7=105 Mi = M/mi M 1=105/3 =35 M 2= 105/5 =21 M 3 =105/7=15 On sait que Yi Mi ≡ 1 mod mi ou Yi ≡ Mi -1 mod mi on a donc d’après Euclide étendue : Y 1=U 1=2 , Y 2=U 2=1 , Y 3=U 3=1 Finalement on obtient donc : X=(a 1 M 1 Y 1 + a 2 M 2 Y 2 + a 3 M 3 Y 3) modulo 105 X=(2*35*2+ 3*21*1+ 2*15*1) modulo 105 X= 233 modulo 105 X = 23 mod 105

Parmi ces 3 Méthodes laquelle est la plus fiable Quelles chemin faut’il prendre ?

COMPARAISON DES DIFFERENTS METHODES A SAVOIR 3 méthodes Méthode : A Méthode : B Méthode : C

Cas particulier Si les Mi ne sont pas premier entre eux ? ? ? ?

Soit l’exemple suivant : X=8 mod 12 X=11 mod 15 X= 0 mod 4 X= 2 mod 3 X=1 mod 5

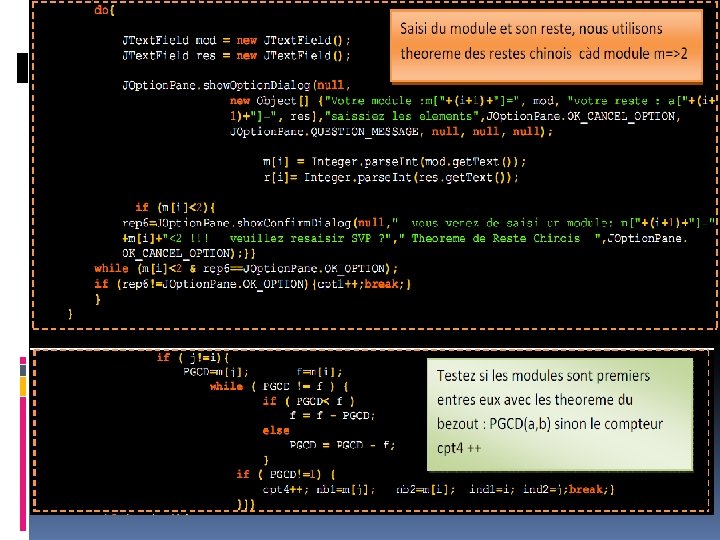
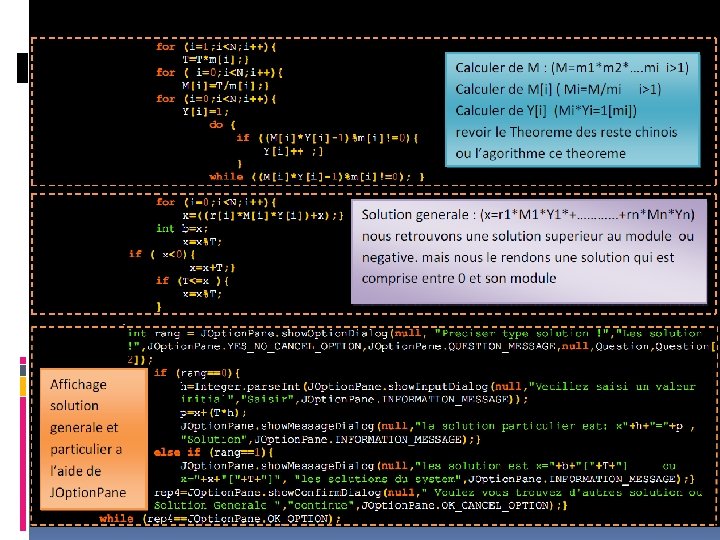
Algorithme

PROGRAMMER EN JAVA

PROGRAMMER C++

Programmer en Java Script

Clôture