The PCP Theorem via gap amplification Irit Dinur


![Definitions PCP [r, q] The probability upon the random coins LЄPCP [r, q] if Definitions PCP [r, q] The probability upon the random coins LЄPCP [r, q] if](https://slidetodoc.com/presentation_image/1878060af15cce1eddefa2e3f0fdd106/image-3.jpg)
![PCP Theorem NP = PCP½[log(n), O(1)] If x L π Pr[v accepts π] = PCP Theorem NP = PCP½[log(n), O(1)] If x L π Pr[v accepts π] =](https://slidetodoc.com/presentation_image/1878060af15cce1eddefa2e3f0fdd106/image-4.jpg)
![What is it good for? NP = PCP½[log(n), O(1)] Gap 3 -SAT[ , 1] What is it good for? NP = PCP½[log(n), O(1)] Gap 3 -SAT[ , 1]](https://slidetodoc.com/presentation_image/1878060af15cce1eddefa2e3f0fdd106/image-5.jpg)

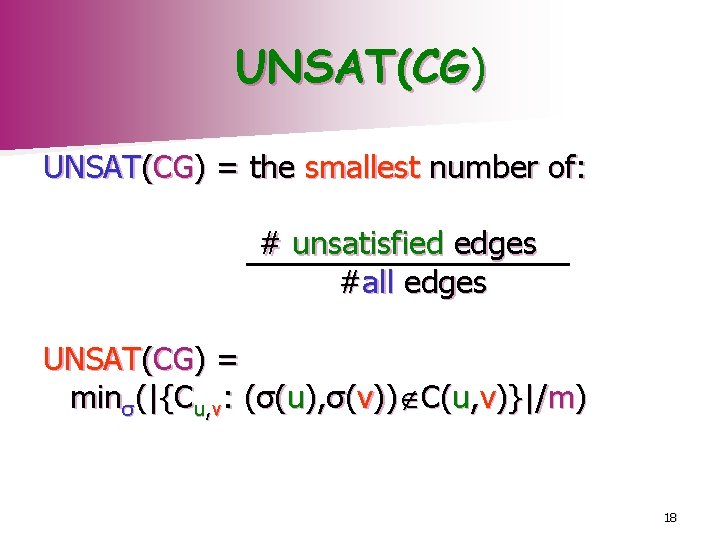
![UNSAT(CG) why? => Gap. CG[1 - , 1] NP-Hard => Gap. CG[1 - , UNSAT(CG) why? => Gap. CG[1 - , 1] NP-Hard => Gap. CG[1 - ,](https://slidetodoc.com/presentation_image/1878060af15cce1eddefa2e3f0fdd106/image-8.jpg)
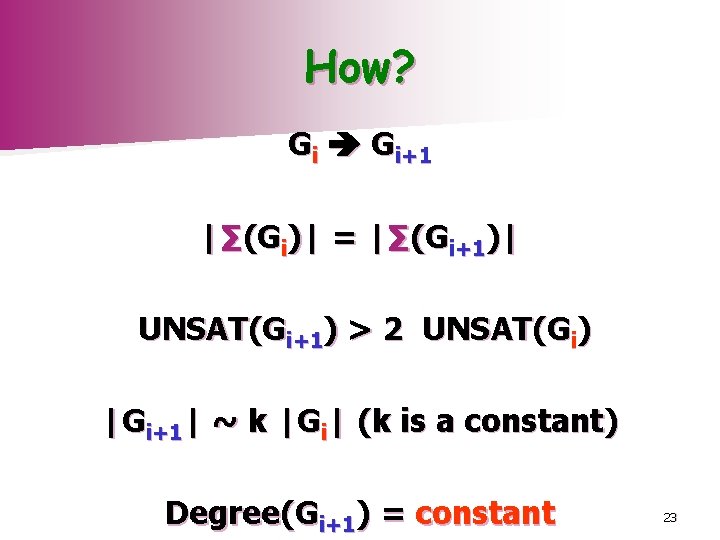










![summary CG NPC CG = Gap. CG[1 -1/m, 1] Gap. CG[1 - 1/m , summary CG NPC CG = Gap. CG[1 -1/m, 1] Gap. CG[1 - 1/m ,](https://slidetodoc.com/presentation_image/1878060af15cce1eddefa2e3f0fdd106/image-22.jpg)
- Slides: 22

The PCP Theorem via gap amplification Irit Dinur Presentation by Michal Rosen & Adiv 1

PCP Prover: gives a proof: 1 0 0 1 Hide it, and gives it to the verifier Verifier: picks constant number of cells randomly Accept/reject according the check 5
![Definitions PCP r q The probability upon the random coins LЄPCP r q if Definitions PCP [r, q] The probability upon the random coins LЄPCP [r, q] if](https://slidetodoc.com/presentation_image/1878060af15cce1eddefa2e3f0fdd106/image-3.jpg)
Definitions PCP [r, q] The probability upon the random coins LЄPCP [r, q] if there is a protocol <p, v>: s. t. if x L π Pr[v accepts π] = 1 if x L π Pr[v accepts π] ≤ r – how many coins does v need for checking π q – the number of places v samples π 6
![PCP Theorem NP PCP½logn O1 If x L π Prv accepts π PCP Theorem NP = PCP½[log(n), O(1)] If x L π Pr[v accepts π] =](https://slidetodoc.com/presentation_image/1878060af15cce1eddefa2e3f0fdd106/image-4.jpg)
PCP Theorem NP = PCP½[log(n), O(1)] If x L π Pr[v accepts π] = 1 If x L π Pr[v accepts π] ≤ ½. r = log(n) - how many coins does v need for checking π q = O(1) - the number of places v samples π 9
![What is it good for NP PCP½logn O1 Gap 3 SAT 1 What is it good for? NP = PCP½[log(n), O(1)] Gap 3 -SAT[ , 1]](https://slidetodoc.com/presentation_image/1878060af15cce1eddefa2e3f0fdd106/image-5.jpg)
What is it good for? NP = PCP½[log(n), O(1)] Gap 3 -SAT[ , 1] NP-Hard PCP is very important for approximate problems 10

Constraint Graph (CG) Input: <G=(V, E), ∑, C >: G = (V, E) undirected graph , ∑ alphabet, C constraints where for every e E, Ce ∑х∑. Example: v=0 ∑ = {0, 1, 2} U=2 1 1, 0 ( , ) 1 (2, )} V { = C u, v U 13
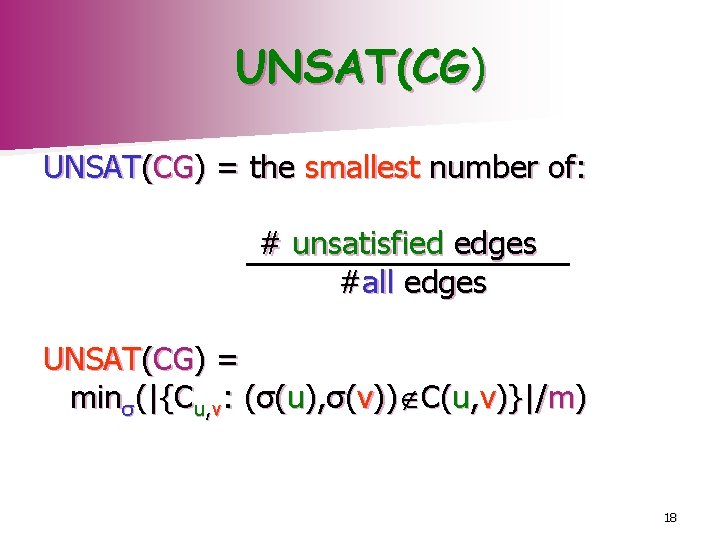
UNSAT(CG) = the smallest number of: # unsatisfied edges #all edges UNSAT(CG) = minσ(|{Cu, v: (σ(u), σ(v)) C(u, v)}|/m) 18
![UNSATCG why Gap CG1 1 NPHard Gap CG1 UNSAT(CG) why? => Gap. CG[1 - , 1] NP-Hard => Gap. CG[1 - ,](https://slidetodoc.com/presentation_image/1878060af15cce1eddefa2e3f0fdd106/image-8.jpg)
UNSAT(CG) why? => Gap. CG[1 - , 1] NP-Hard => Gap. CG[1 - , 1] ≤p Gap 3 -SAT[c, 1] => Gap 3 -SAT[c, 1] NP-Hard => PCP theorem!!! Remember: NP = PCP½[log(n), O(1)] Gap 3 -SAT[c, 1] NP-Hard 21
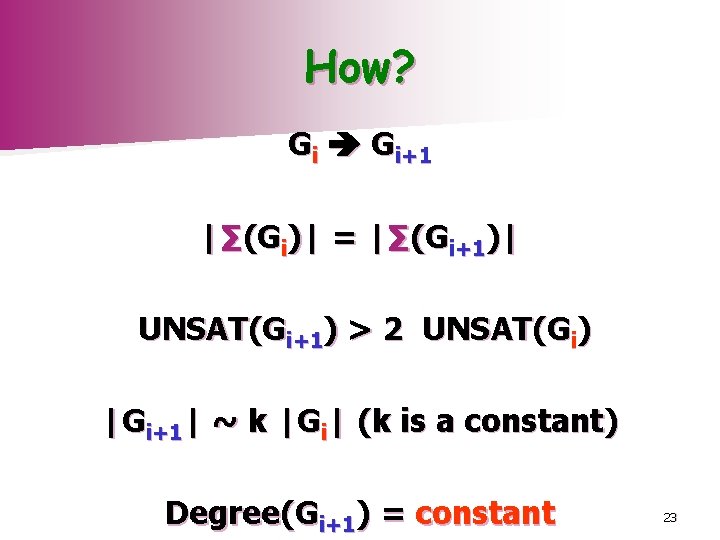
How? Gi Gi+1 |∑(Gi)| = |∑(Gi+1)| UNSAT(Gi+1) > 2 UNSAT(Gi) |Gi+1| ~ k |Gi| (k is a constant) Degree(Gi+1) = constant 23

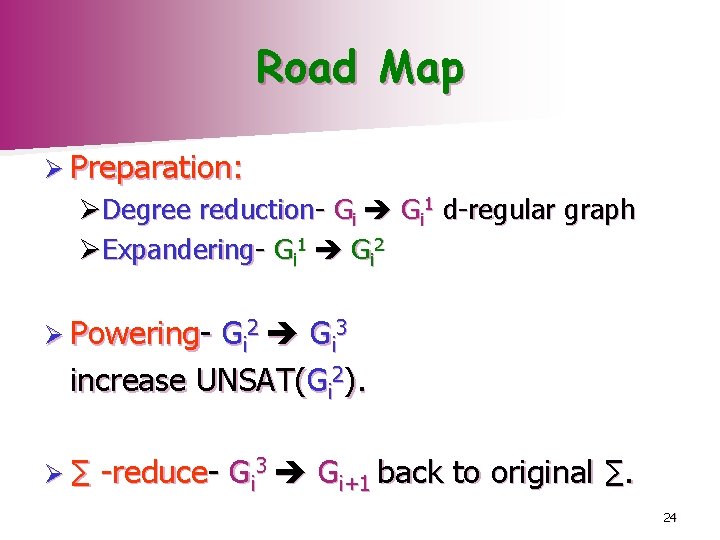
Road Map Ø Preparation: ØDegree reduction- Gi 1 d-regular graph ØExpandering- Gi 1 Gi 2 Ø Powering- G i 2 G i 3 increase UNSAT(Gi 2). Ø∑ -reduce- Gi 3 Gi+1 back to original ∑. 24

Preparation After the preparations the graph becomes d-regular expander. We’ll see later how to do it. UNSAT(G) |G| Constant factor Deg(G) |∑| Constant factor d-regular No change 25

Powering - overview Result: UNSAT(Gt) ≥ β √t UNSAT(G) Problem: |∑| becomes |∑|d^t UNSAT(G) |G| Constant factor Deg(G) |∑| Constant factor goes up (problem!!!)26

Powering Lemma (amplification lemma) β > 0, G = <(V, E), ∑, C> - d-regular-CG UNSAT(Gt) ≥ β√tmin(UNSAT(G), 1/t) Example: If we’ll take t ≥ 4/β 2 then UNSAT(Gt) ≥ 2 UNSAT(G) or 1/t (constant) 31

Powering What does it give us? UNSAT(G) = 1/m 22/m … 2 O(log(m))/m = We need to repeat the procedure O(log(m)) times 32

Reduce ∑ Problem: ∑ is exponential in n - ∑d^log(n). The reduction won’t be polynomial. Solution: There is a code no change UNSAT(G) that reduce ∑ |G| by constant Deg(G) |∑| by constant back to usual 34

Summary In each iteration (3 steps combined) Preparations, Powering and Reduce ∑ n Doubles UNSAT n Increases |G| by constant factor. n Increases degree. n Doesn’t change ∑. 35

More about Expandering Problem: what if we have this graph? F – satisfied edges S – unsatisfied C edges C – the edges 0 between T to S } ) 1, 0 1 0 U U {( C u. v = )} {(1, 0 = C u. v V 0 V F S 47

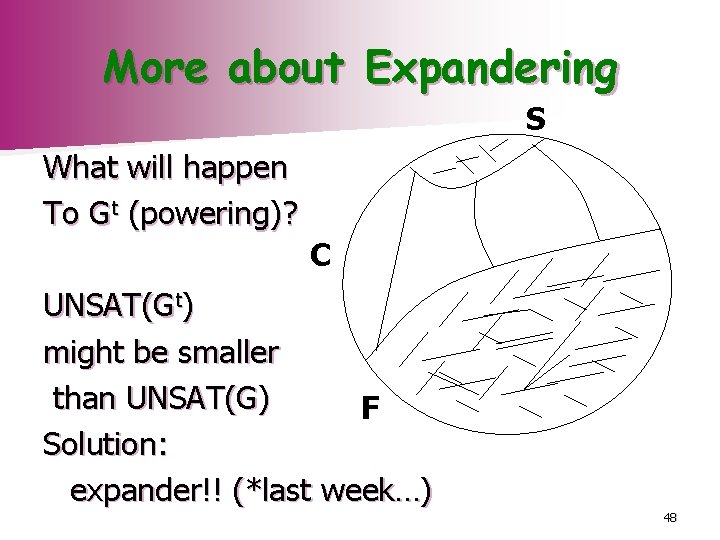
More about Expandering S What will happen To Gt (powering)? C UNSAT(Gt) might be smaller than UNSAT(G) F Solution: expander!! (*last week…) 48

More about Expandering Definition: G is expander if for every S in V s. t. |S| ≤ |V|/2, denote E(S, S’) as the number of edges between S to V/S (=S’), a|S| ≤ E(S, S’), where a > 1. 49

More about Expandering Why is expander a solution? Denote S as the “bad” edges (unsatisfied edges). In every power iteration S multiplies itself in a constant > 1. S (1+a/d)2 S … (1+a/d)O(log(m))S ≈ m So after O(log(m)) iterations we get to all the edges. 50

Preparation - summary After the preparations the graph becomes d-regular expander. We’ll see later how to do it. UNSAT(G) |G| Constant factor Deg(G) |∑| Constant factor d-regular No change 51
![summary CG NPC CG Gap CG1 1m 1 Gap CG1 1m summary CG NPC CG = Gap. CG[1 -1/m, 1] Gap. CG[1 - 1/m ,](https://slidetodoc.com/presentation_image/1878060af15cce1eddefa2e3f0fdd106/image-22.jpg)
summary CG NPC CG = Gap. CG[1 -1/m, 1] Gap. CG[1 - 1/m , 1] p(polytime) Gap. CG[ , 1] NP-Hard Gap. CG[ , 1] ≤p Gap 3 -SAT[ ’, 1] NP-Hard PCP theorem!!! 52