The Monte Carlo Method Markov Chains Metropolitan Algorithm

The Monte Carlo Method/ Markov Chains/ Metropolitan Algorithm from sec. 2. 9 -2. 11 in “Adaptive Cooperative Systems” -summarized by Jinsan Yang

2. 9 The Monte Carlo Method n Definition ¨ Monte Carlo method is a device for studying stochastic models ¨ Introduced by Ulam and von Neumann in 1947 for solving integral and differential equations ¨ It is easier to solve numerically to an equation by finding stochastic process and computing the resulting statistics than to solve the equation directly ¨ The use of a random sampling method for the solution of a deterministic mathematical problem

n Study of Reaction Processes ¨ Monte Carlo method for the oxygen-carbon reactions ¨ Emission probabilities for six particle species were computed and compared to a uniformly distributed random number to determine which particle type would be emitted ¨ Candidate energy was accepted if the probability for emitting a particle with the proposed energy was greater than another random number, else was rejected and these process was repeated until an energy was selected

n Problems in Statistical Mechanics ¨ The Monte Carlo method was extended by Metropolis et al in 1953 to statistical mechanics to determine properties of substances of multiple interacting elements ¨ In direct manner, every possible configuration of the N -molecule system should be included. ¨ In Monte Carlo method, the summation is carried out by choosing a configuration at random and weight by appropriate Boltzmann factor ¨ In the approach of Metropolis et al, a molecule was selected and a small displacement was conducted by a uniformly drawn random number. If the corresponding energy change was greater than a random number, the change was permitted and the procedure was repeated.

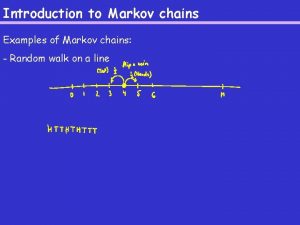
2. 10 Markov Chains n Definitions ¨ In an array of N elements, each element can be up/down state and for each unique configuration of the array corresponds a random variable: energy or magnetization of the system. ¨ Collection of configuration points for X=xi is referred to as the state X=xi ¨ Can extend these definitions to two or more random variables

¨ Transition ¨ Probabilities Markov chain

n Convergence to stationary distributions ¨ Irreducible MC: if there is no closed collection other than the collection of all states (every state can be reached from every other states) ¨ A probability distribution {wi} is stationary if ¨ Convergence theorem for irreducible and aperiodic MC: n-step transition probabilities will approach a unique stationary distribution if stationary distribution exists (influence of initial state will disappear) ¨ (stationary distribution does not exist)

n Convergence to stationary distributions ¨ condition of detailed balance relation : ¨ Under above condition, the probability distribution is stationary ¨ Goals of metropolis et al. n Avid explicit evaluation of the partition function n Efficient MC sampling by picking configuration relative to the importance n To achieve these, transition probabilities are defined with balance relation and with Gibbs distribution as the stationary distribution

2. 11 The Metropolis Algorithm n MC with three priori transition probability conditions: n Define transition probability n Gibbs distribution

n Transition probabilities obey the detailed balance relation n Limiting stationary distribution reached by the n-step transition probabilities is unique and therefore the stationary distribution generated by the Metropolis algorithm must be the Gibbs distribution.

n Metropolis sampling procedure ¨ At time t, the state X takes the value xt , and select a state Yt at random from the target distribution in a manner which satisfies the symmetry condition ¨ Energy difference If the energy difference is negative, transition is allowed ¨ If the energy difference is positive, select a random number r between 0 and 1 and if allow the transition ¨